沪教版（五四制）（2024）八年级上册19．1 命题和证明优秀教学课件ppt

这是一份沪教版（五四制）（2024）八年级上册19．1 命题和证明优秀教学课件ppt，共40页。PPT课件主要包含了题设条件，已知事项，已知事项推出的事项，“如果那么”，和结论，两条直线相交，它们只有一个交点，∠1∠3，真命题，假命题等内容，欢迎下载使用。
1、进一步了解证明的基本过程。2、能将几何命题的文字评语言用图形语言和符号语言表示出来。3、经历探索推理的论证过程，感受几何中的逻辑推理的内涵及几何证明的基本形式。4、培养严谨的证明意识，提高思维能力，初步感受推理的严密性、条理性。
19.1 演绎证明（第1课时）
问1：怎样才算严格的数学证明呢？
问2：你会用哪些方法来导出“对顶角相等”？
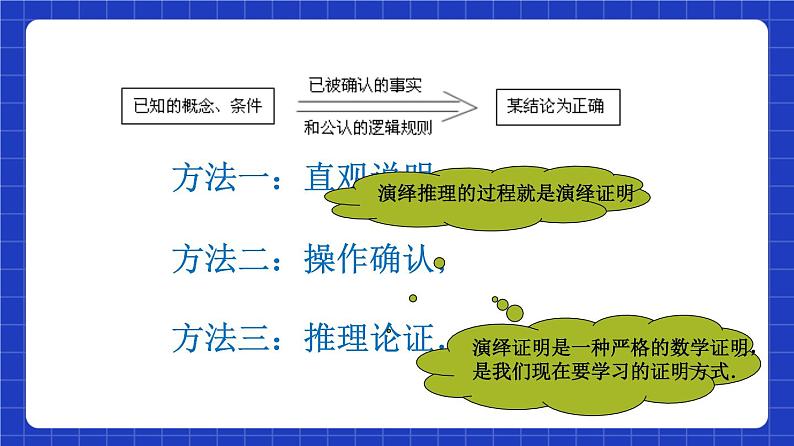
方法一：直观说明； 方法二：操作确认；方法三：推理论证．
∵∠1与∠2是邻补角（已知），∴∠1＋∠2＝180°（邻补角的意义），∵∠1与∠3是邻补角（已知），∴∠1＋∠3＝180°（邻补角的意义），∴∠2＝∠3（同角的补角相等）．
问3：这些方法中，哪一种最可靠、最有说服力？
演绎推理的过程就是演绎证明
演绎证明是一种严格的数学证明，是我们现在要学习的证明方式．
演绎证明是指: 从已知的概念 、条件出发，依据已被确认的事实和公认的逻辑规则推导出某结论为正确的过程。
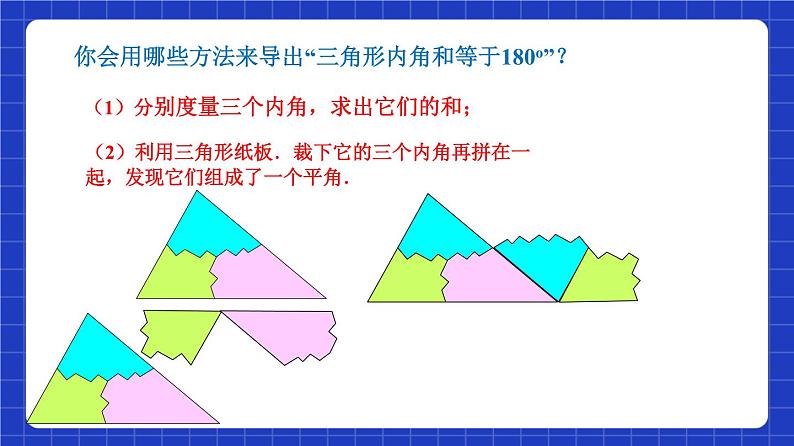
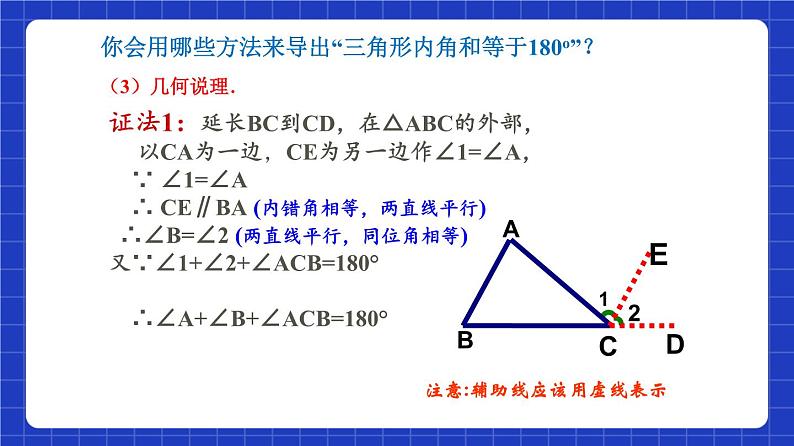
你会用哪些方法来导出“三角形内角和等于180”？
（2）利用三角形纸板．裁下它的三个内角再拼在一起，发现它们组成了一个平角．
（1）分别度量三个内角，求出它们的和；
证法1：延长BC到CD，在△ABC的外部， 以CA为一边，CE为另一边作∠1=∠A， ∵ ∠1=∠A ∴ CE∥BA (内错角相等，两直线平行) ∴∠B=∠2 (两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180° ∴∠A+∠B+∠ACB=180°
证法2：延长BC到D，过C作CE∥BA， ∵ CE∥BA ∴ ∠A=∠1(两直线平行，内错角相等) ∠B=∠2(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180° ∴∠A+∠B+∠ACB=180°
证法3：过A作EF∥BA， ∵ EF∥BA ∴∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) 又 ∵∠2+∠1+∠BAC=180° ∴∠B+∠C+∠BAC=180°
演绎证明的每一步推理都必须有依据通常把每一步的依据写在由其得到的结论后面的括号内整个证明由一段一段的因果关系连接而成段与段前后连贯，有序展开．
已知：如图，∠AOC与∠COB互为邻补角，OD平分∠AOC，OE平分∠COB．求证：∠DOE=90．
1. 阅读下面的证明过程，说一说其中的因果关系．
2.已知：如图，点D、E、F分别在△ABC的边BC、AB、AC上，且DF∥AB，DE∥AC，试利用平行线的性质证明∠A+∠B+∠C=180°
证明：∵DF∥AB（已知），∴∠B=∠FDC（两直线平行，同位角相等），同理，∠C=∠EDB，∵DE∥AC（已知），∴∠A=∠DEB（两直线平行，同位角相等），∵DF∥AB（已知），∴∠DEB=∠EDF（两直线平行，内错角相等），∴∠A=∠EDF（等量代换），∵∠FDC +∠EDF+∠EDB =180°（平角的意义），∴∠B+∠A+∠C=180°（等量代换），即∠A+∠B+∠C=180°
1．审题： 分清命题的“条件”和“结论”。
4．证明： 不管你用什么方法分析都要从已知出发，每一步过程要有依据（定义、公理、定理）最后得到结论，全面推理过程要因果分明。
3．想题： 用“由因索果”（综合法）；或用“由果索因”（分析法）寻找论证推理逻辑思路。一般是把二者结合起来思考，效果较好，这也叫综合分析法。
2．译题： ①作出图形并在图上标出必要的字母或符号。（有时图已给出）②结合图形中字母及符号，写出已知，求证。
19.1 命题、公理、定理（第2课时）
(1)能够被2整除的数叫做偶数。(2)互为补角的两个角都是锐角。(3)对顶角相等。(4)如果两条直线都与第三条直线平行，那么这两条直线也互相平行。(5)画∠AOB的平分线OC。(6)等角的余角相等吗？
判断一件事情的句子叫做命题。判断为正确的 命题叫做真命题， 判断为错误的命题叫做假命题。
请说出下列名词的定义：⑴无理数：⑵直角三角形：⑶素数：⑷一元一次方程：
无限不循环小数叫做无理数。
有一个角是直角的三角形叫做直角三角形。
只能被1和本身整除的数叫做素数。
只含有一个未知数，且未知数的最高次数是1的整式方程叫做一元一次方程。
2）两条直线相交，有且只有一个交点.（ ）
4）一个平角的度数是180度.（ ）
6）取线段AB的中点C.（ ）
1）长度相等的两条线段是相等的线段吗?( )
7）画两条相等的线段.（ ）
判断下列语句是不是命题？如果是命题并请判断真假.
3）不相等的两个角不是对顶角.（ ）
5）南京是中国的首都.（ ）
判断一个句子是不是命题的关键是什么？
观察下列命题，你能发现这些命题有什么共同的结构特征？（1）如果两个三角形的三条边相等，那么这两个三角形全等；（2）如果一个三角形是等腰三角形，那么这个三角形的两个底角相等；（3）如果一个四边形的对角线相等，那么这个四边形是矩形；
命题的结构：在数学中，许多命题是由 两部分组成的. 是 ， 是由 . 这种命题常可写成 的形式,“如果”开始的部分是题设,“那么”开始的部分是结论.
指出下列命题的题设和结论:
∠1=∠2，∠2=∠3
两条平行线被第三条直线所截
两条直线被第三条直线所截，同旁内角互补
　 将下列命题改写成“如果…那么…”的形式，并指出命题的条件和结论：⑴同位角相等，两直线平行；⑵三条边对应相等的两个三角形全等；
　　如果同位角相等，那么两直线平行。
条件是：结论是：改写成：
　　如果两个三角形有三条边对应相等，那么这两个　　三角形全等。
两个三角形的三条边对应相等
　（3）在同一个三角形中，等角对等边； （4）对顶角相等。
　　如果在同一个三角形中，有两个角相等，那么这两个角所对的边也相等。
如果两个角是对顶角，那么这两个角相等。
在同一个三角形中，有两个角相等
这两个角所对的两条边相等
将下列命题改写成“如果……，那么……”的形式，并判断其真假。
(2)形状和大小相同的两个三角形面积相等.
如果两个角是同位角，那么这两个角相等。
如果两个三角形的形状和大小相同，那么这两个三角形面积相等。
(3)三个角都相等的三角形是等边三角形
如果一个三角形的三个角都相等，那么这个三角形是等边三角形。
(4)全等三角形的对应边相等；
如果两个三角形全等，那么它们的对应边相等。
(5)两条边和它们的夹角对应相等的两个三角形全等；　　(6)直角三角形两个锐角互余。
　如果两个三角形有两条边和它们的夹角对应相等，那么这两个三角形全等。
　　如果两个角是一个直角三角形的两个锐角，那么这两个角互余。
讨论：我们如何说明一个命题的真假？
要说明一个命题是真命题需要推理论证；要说明一个命题是假命题只要举一个反例即可。
反例：符合命题条件，但不符合命题结论的例子。
证明：“相等的两个角是对顶角”是假命题。
证明：如图，∠1=30°，∠2=30°，但∠1与∠2不是对顶角。
判断下列命题是真命题还是假命题，如果是假命题，请证明：
（1）若∣a∣=∣b∣,则a=b；
（2）如果ab>0，那么a、b都是正数；
（3）互为补角的两个角都是锐角。
人们从长期的实践中总结出来的真命题叫做公理，公理可以作为判断其他命题真假的原始依据。
三角形的任何两边之和大于第三边。
两直线平行，同位角相等
两直线平行，内错角相等。
从公理或其它真命题出发，用推理方法证明为正确的、并进一步作为判断其他命题真假的依据，这样的真命题叫做定理。
我们学过的公理有哪些？1.经过两点有且只有一条直线。2.两点之间，直线段最短。3.经过直线外一点，有且只有一条直线和这条直线平行。4.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。5.两条平行线被第三条直线所截，同位角相等。6.有两边和它们的夹角对应相等的两个三角形全等。7.有两角和它们的夹边对应相等的两个三角形全等。8.有三边对应相等的两个三角形全等。
公理和定理的共同点和不同点： 共同点：都是真命题 不同点：公理的正确性是人们长期实践检验所证实的，定理的正确性是依赖推理证实的.
定义、公理和定理，都是用推理方法判断命题真假的依据。
1.请举出一些命题,并判断命题的真假.2。指出下列命题的题设和结论,并判断命题的真假:同旁内角相等,两直线平行,(2) 全等三角形的对应边相等.(3) 在同一平面内，垂直于同一条直线的两条直线互相平行.(4)在一个三角形中,等边对等角.(5) 关于某个点中心对称的两个三角形全等.(6)等角的补角相等.
1.下列句子哪些是命题？是命题的，指出是真命题还是假命题？
1、猪有四只脚；2、三角形两边之和大于第三边；3、画一条曲线；4、四边形都是菱形；5、你的作业做完了吗？ 6、同位角相等，两直线平行；7、对顶角相等；8、多边形的内角和等于180度；9、过点P做线段MN的垂线。
2.判断下列命题的真假：1)如果x=0,那么xy=0;2)如果x2=y2,那么x=y;3)对顶角相等；4)相等的角是对顶角；5)如果︱x︱=2,那么x=2;6)-a表示的一定是负数.
（1）“两负数之积为正数” 题设是 ， 结论是 ；（2）两点之间，线段最短 改写成“如果 ， 那么 ”
（3）如果两个角互补，那么它们是 邻补角。它是 命题
这些线中，线段最短
1、命题：判断一件事情的语句叫命题。
2、公理：人们长期以来在实践中总结出来的，并作为判断其他命题真假的根据的命题，叫做公理。
3、定理：经过推理论证为正确的命题叫定理。也可作为继续推理的依据。
4、判断一个命题是真命题，可以从公理或定理出发，用逻辑推理的方法证明（公理和定理都是真命题）； 判断一个命题是假命题，只要举出一个例子，说明该命题不成立就可以了，这种方法称为举反例。
（1）正确的命题称为真命题，错误的命题称为假命题。（2）命题的结构：命题由题设和结论两部分构成，常可写成“如果…，那么…”的形式。