沪教版（五四制）（2024）19．9 勾股定理公开课教学ppt课件

这是一份沪教版（五四制）（2024）19．9 勾股定理公开课教学ppt课件，共24页。PPT课件主要包含了勾股定理，勾股定理的由来等内容，欢迎下载使用。
1．体验勾股定理的探索过程,掌握勾股定理并能简单运用2．经历“观察—猜想—归纳—验证”的数学过程，体会数形结合的数学思想和由特殊到一般的研究问题方法.3．了解中国古代在勾股定理方面的成就，知道勾股定理在人类重大科技发现中的地位.
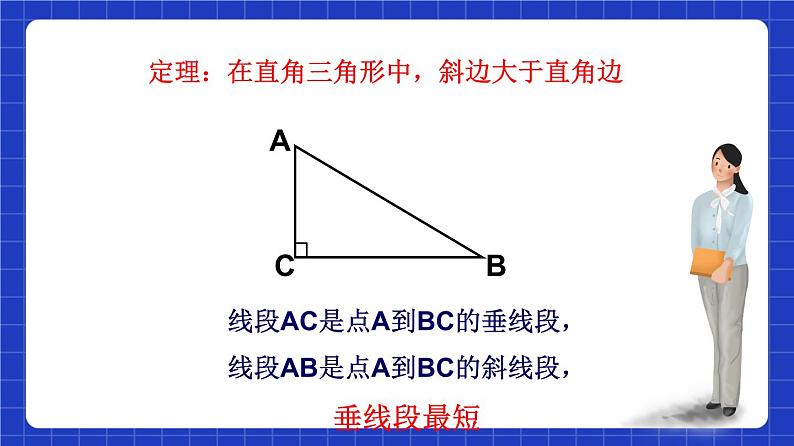
线段AC是点A到BC的垂线段，线段AB是点A到BC的斜线段，垂线段最短
问题1 在直角三角形中，斜边与两条直角边之间有怎样的大小关系？为什么？
定理：在直角三角形中，斜边大于直角边
问题1 在直角三角形中，斜边和两条直角边之间有没有某种等量关系？
请用两个大小相同的小正方形，通过割补把它拼成一个大正方形。
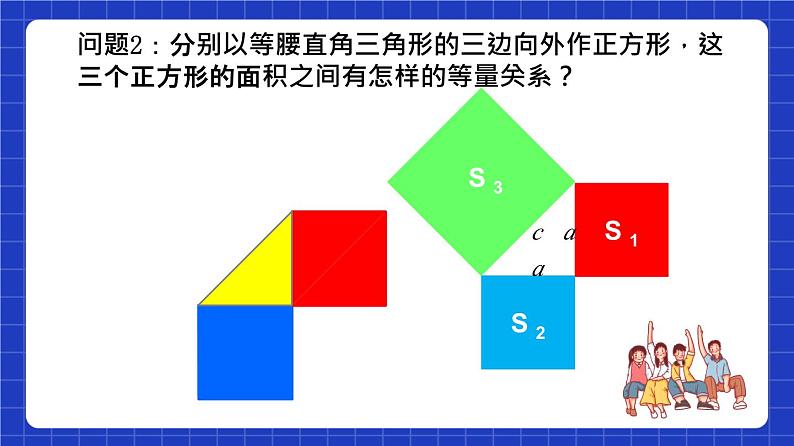
问题2：分别以等腰直角三角形的三边向外作正方形，这三个正方形的面积之间有怎样的等量关系？
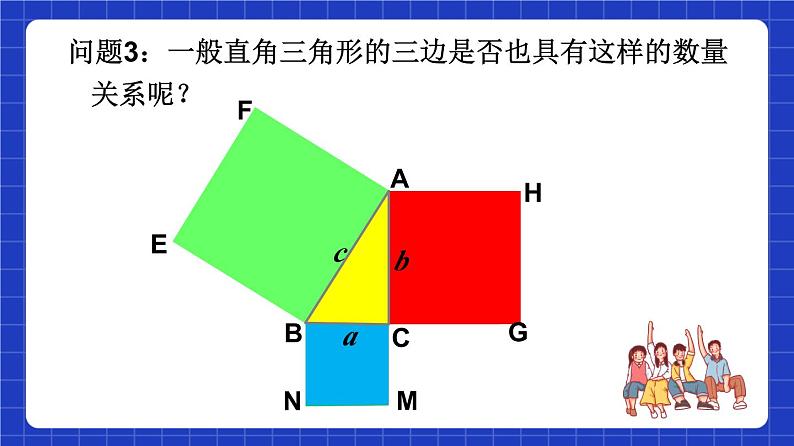
问题3：一般直角三角形的三边是否也具有这样的数量关系呢？
如图是用硬纸板做成的四个两直角边长分别是a，b，斜边长为c的全等的直角三角形和一个边长为c的正方形，请你将它们拼成一个能说明勾股定理正确性的图形． (1)画出拼成的这个图形的示意图； (2)说明勾股定理的正确性． 
分析：可以以边长为c的正方形为基础，一在形外补拼(不重叠)成新的正方形；二在形内叠合成新的正方形．
解：方法一(补拼法)：(1)如图. (2)因为大正方形的面积可以表示为(a＋b)2， 也可以表示为c2＋4× ab， 所以(a＋b)2＝c2＋4× ab， a2＋b2＋2ab＝c2＋2ab.
所以a2＋b2＝c2， 即直角三角形两直角边的平方和 等于斜边的平方．
方法二(叠合法)：(1)如图.(2)因为大正方形的面积可以表示为c2， 也可以表示为 ab×4＋(b－a)2， 所以c2＝ ab×4＋(b－a)2，c2＝2ab＋b2－2ab＋a2. 所以a2＋b2＝c2， 即直角三角形两直角边的平方和等于斜边的平方．
定义：直角三角形两直角边的平方和等于斜边的平方．如果用a，b和c分别表示直角三角形的两直角边和斜边，那么a2＋b2＝c2.数学表达式：在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，则a2＋b2＝c2.
a 2 + b 2 = c 2
较短直角边为勾，长直角边为股，斜边为弦，因此称作“勾股定理”公元前 1000 多年，《周髀算经》 “商高定理”公元前五百多年，“毕达哥拉斯定理”、“百牛定理”
a b
我国古代数学家的巧妙证法
a b
a b
求边长为1的等边三角形的面积。
已知： ⊿ABC中，AB=BC=CA=1,求三角形ABC的面积。
解：作AD⊥BC，垂足为D.
∵AB=AC=BC=1,AD⊥BC∴BD=CD=1/2(等腰三角形三线合一)
在Rt⊿ABD中，∵∠ABD=90°(垂直定义)， ∴AB2=AD2+BD2(勾股定理)
1.在 Rt△ABC中，∠A=90°,设 a、b、c 分别表示∠A、∠B、∠C所对的边(1)已知b=4,c=5,求 a;(2)已知a=13,6=12,求c
2.已知等腰直角三角形的腰长为 5,求这个三角形的周长.
3.求下列图中字母所表示的正方形的面积
1.若一个直角三角形的两直角边的长分别为a，b，斜边长为c，则下列关于a，b，c的关系式中不正确的是(　　) A．b2＝c2－a2 B．a2＝c2－b2 C．b2＝a2－c2 D．c2＝a2＋b2
2.如图，在边长为1个单位长度的小正方形组成的网格中，点A，B都是格点，则线段AB的长度为(　　) A．5 B．6 C．7 D．25
3.用四个边长均为a，b，c的直角三角板，拼成如 图所示的图形，则下列结论中正确的是(　　) A．c2＝a2＋b2 B．c2＝a2＋2ab＋b2 C．c2＝a2－2ab＋b2 D．c2＝(a＋b)2
4.两棵树之间的距离为8 m，两棵树的高度分别是8 m，2 m，一只小鸟从一棵树的树顶飞到另一棵树的树顶，这只小鸟至少要飞多少米？
解：根据题意画出示意图，如图所示， 两棵树的高度分别为AB＝8 m，CD＝2 m， 两棵树之间的距离BD＝8 m， 过点C作CE⊥AB，垂足为E，连接AC. 则BE＝CD＝2 m，EC＝BD＝8 m， AE＝AB－BE＝8－2＝6(m)． 在Rt△ACE中，由勾股定理，得AC2＝AE2＋EC2， 即AC2＝62＋82＝100，所以AC＝10 m. 答：这只小鸟至少要飞10 m．
分析：先根据题意画出图形，然后添加辅助线，构造直角三角形，再利用勾股定理求解．
5.我方侦察员小王在距离东西向公路400m处侦察，发现一辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪，测得汽车与他相距400m，10s后，汽车与他相距500m,你能帮小王计算敌方汽车的速度吗？
由于小王距离公路400m，因此∠C是直角，这样就可以由勾 股定理来解决这个问题了.
解：由勾股定理，可以得到AB2=BC2+AC2， 也就是5002=BC2+4002, 所以BC=300.敌方汽车10s行驶了300m， 那么它1h行驶的距离为300×6×60=108000（m）, 即它行驶的速度为108km/h.
分析：根据题意，可以画出右图，其中点A表示小王所在位置，点C、点B表示两个时刻敌方汽车的位置.
1．学习内容方面：勾股定理及其公式应用；
2．数学思想方面：数形结合、特殊到一般、面积法。
3.情感方面：中国人有智慧，数学很有用，数学很美。