





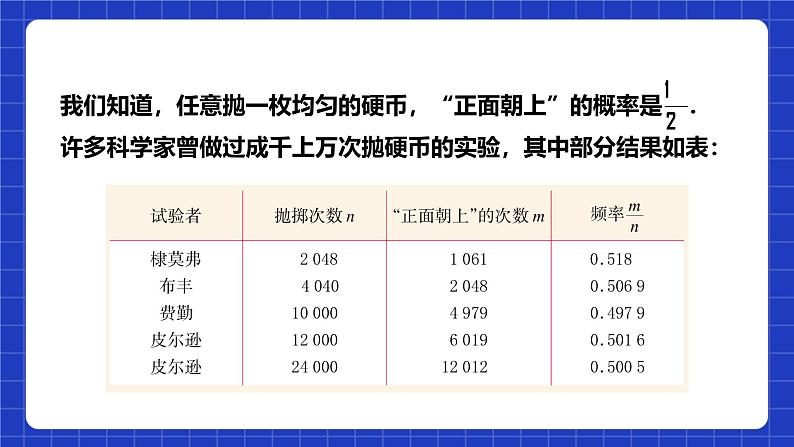



所属成套资源:浙教版数学九上课件PPT+教案整套(含单元教案)
初中数学浙教版(2024)九年级上册第2章 简单事件的概率2.3 用频率估计概率优秀ppt课件
展开
这是一份初中数学浙教版(2024)九年级上册第2章 简单事件的概率2.3 用频率估计概率优秀ppt课件,文件包含浙教版数学九上23《用频率估计概率》课件ppt、浙教版数学九上23《用频率估计概率》教学设计doc等2份课件配套教学资源,其中PPT共34页, 欢迎下载使用。
本节课是浙教版九年级上册第二章第三节的内容,它是学习了前两节概率和列举法求概率的基础上,进一步从试验角度估计概率,让学生再次体会频率与概率之间的关系,体现了新课标中第三学段“统计与概率”中对两个重要概念“频率、概率”的要求。通过对这部分内容的学习可以帮助学生进一步理解实验频率和理论概率的关系,对此内容的学习,也是为高中深入学习概率的相关知识打下基础。
1.理解每次试验可能结果不是有限个,或各种可能结果发生的可能性不相等时,用频率估计概率的方法.2.能应用模拟实验求概率及其它们的应用.3.理解“当试验次数较大,实验频率稳定于理论概率,并可据此估计某一事件发生的概率”.
重点:掌握实验的方法估计复杂的随机事件发生的概率。难点:试验估计随机事件发生的概率,关键是通过试验,统计活动,体会随机事件的概率。
想一想:400个同学中,一定有2个同学的生日相同(可以不同年)吗?
一年最多366天, 400个同学中一定会出现至少2人出生在同月同日。
想一想:300个同学中,一定有两个同学的生日相同吗?
想一想:提高运动员的罚球命中率是篮球教练需考虑的问题之一. 你认为可以如何估计一位篮球运动员的罚球命中率?
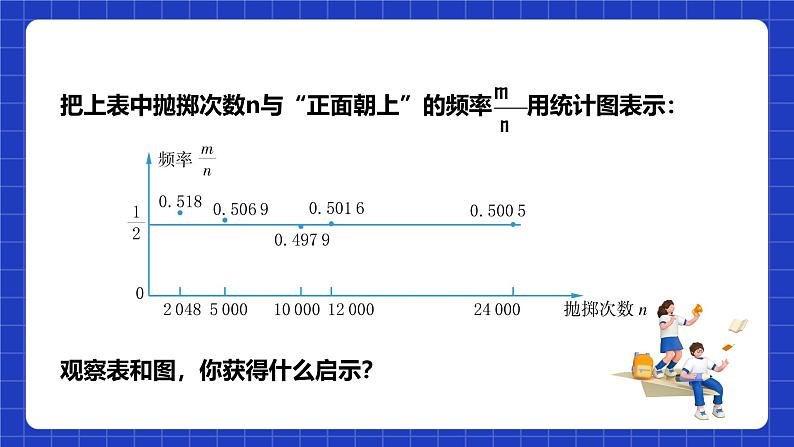
观察表和图,你获得什么启示?
【总结归纳】当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
【合作学习】做抛掷两枚硬币的试验. 观察它们落地时出现“一正一反”的次数.
1. 全班每人各取两枚同样的硬币,做 10 次掷硬币的试验,填入表
2.将每个小组同学的试验结果进行统计,填入表.
3.将其中两组同学的试验结果进行统计,填入表.
4.将其中 4 组同学的试验结果进行统计,填入类似统计表.5.统计全班同学的试验结果,填入类似统计表. 根据上述统计表画出“一正一反”的频率统计图.
议一议:频率与概率有什么区别和联系?随着重复实验次数的增加,频率的变化趋势如何?
从上面的实验可以看到:在相同条件下,当重复实验的次数大量增加时,事件发生的频率就稳定在相应的概率附近. 因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率.
【例】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表。
(1)计算表中的各个频率.
(2)估计该麦种的发芽概率.
解:由第(1)题可知,该麦种的发芽概率约为 0.95.
(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87%,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少千克(精确到1kg)?
【总结归纳】大量的实验表明:当重复实验的次数大量增加时,事件发生的频数就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率. 因此,我们一般把实验次数最多的频率近似作为该事件的概率。
【知识技能类作业】 必做题:1.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的数量最有可能是( )A.5B.10C.12D.15
2.表中记录了某种苹果树苗在一定条件下移植成活的情况:
由此估计这种苹果树苗移植成活的概率约为______.(精确到0.1)
3.下列说法合理的是( )A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%B.掷一枚普通的正六面体骰子,出现6点朝上的概率是的意思是每掷6次就有1次掷得6点朝上C.某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
【知识技能类作业】 选做题:4.某射击运动员在同一条件下的射击成绩记录如下:根据频率的稳定性,估计这名运动员射击1次时“射中九环以上”的概率约是( ).A.0.90 B.0.82 C.0.85 D.0.84
5.如图①所示,平整的地面上有一个不规则的图案(图中阴影部分),小明想了解该图案的面积是多少,他采用了以下办法:用一个长为5 m,宽为4 m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的折线统计图,由此他估计不规则图案的面积大约为( ).A.6 m2 B.7 m2C.8 m2 D.9 m2
6.一个不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同.某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
(1)该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是________(精确到0.01),由此估计出红球有________个;
【综合实践类作业】(2)现从该袋中一次摸出2个球,请用画树状图法列出所有等可能的结果,并求恰好摸到1个白球、1个红球的概率.
本节课你学到了哪些知识?
2.方法:用大量重复试验的频率去估计概率.
3.思想:用频率估计概率.
1.频率与概率的关系.
【知识技能类作业】必做题
1.甲、乙两名同学在一次用频率估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是 ( )A.掷一枚正六面体的骰子,出现1点的概率B.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率C.抛一枚硬币,出现正面的概率D.任意写一个整数,它能被2整除的概率
2.某同学抛一枚均匀的硬币,共抛了100次.正面朝上的次数是48次,关于这次试验,下列说法正确的是( )A.正面朝上的频数是100B.正面朝上的频率是20.8%C.正面朝上的频率是48%D.正面朝上的概率是48%
选做题:3.校篮球队队员小亮训练定点投篮以提高命中率,下表是小亮一次训练时的进球情况,下列说法正确的是( )A.小亮每投10个球,一定有8个球进B.小亮投球前8个进,第9、10个一定不进C.小亮比赛中的投球命中率一定为80%D.小亮比赛中的投球命中率可能为100%
4.在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干个,某小组做摸球试验, 将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,不断重复.下表是活动中的一组数据,则摸到黑球的概率约是( )A.0.4 B.0.5 C.0.6 D.0.7
5.庆祝北京冬奥会圆满闭幕,某商场为吸引顾客,设置了一种游戏,其规则如下:凡参与游戏的顾客从一个装有12个红球和若干个白球(每个球除颜色外,其余都相同)的不透明纸箱中,随机摸出1个球,摸到红球就可免费得到1个冬奥会吉祥物(冰墩墩或雪容融).据统计,参与这种游戏的顾客共有60 000人,商场一共为参与该游戏的顾客免费发放了冬奥会吉祥物15 000个.
(1)求参与该游戏可免费得到冬奥会吉祥物的频率.
解:由题意得15 000÷60 000=0.25.答:参与该游戏可免费得到冬奥会吉祥物的频率为0.25.
(2)请你估计纸箱中白球的数量大约有多少?
相关课件
这是一份初中数学浙教版(2024)九年级上册2.3 用频率估计概率完整版ppt课件,文件包含浙教版数学九上23《用频率估计概率》课件ppt、浙教版数学九上23《用频率估计概率》教学设计doc等2份课件配套教学资源,其中PPT共34页, 欢迎下载使用。
这是一份浙教版九年级上册2.3 用频率估计概率优秀课件ppt,文件包含浙教版数学九上23用频率估计概率课件pptx、浙教版数学九上23用频率估计概率学案doc、浙教版数学九上23用频率估计概率教案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
这是一份浙教版九年级上册2.3 用频率估计概率一等奖ppt课件,共20页。PPT课件主要包含了学习目标,问题引入,掷硬币试验,知识精讲,针对练习,典例解析,达标检测,频率与概率的关系,小结梳理等内容,欢迎下载使用。











