数学九年级上册4.3 相似三角形完整版课件ppt

这是一份数学九年级上册4.3 相似三角形完整版课件ppt，文件包含浙教版数学九上453《相似三角形性质的实际应用》课件pptx、浙教版数学九上453《相似三角形性质的实际应用》教学设计doc等2份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
1.能运用相似三角形的性质解决一些简单的实际问题.2.建立相关的相似三角形的模型，然后根据相似三角形的性质以及比例关系解决实际问题.3.通过例题的教学，培养分析问题、解决问题的能力及思维的发散性和灵活性．
我们已经学习了相似三角形的哪些性质？
1.相似三角形对应角相等.2.相似三角形对应边成比例.3.相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.4.相似三角形的周长之比等于相似比.5.相似三角形的面积之比等于相似比的平方.
据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度。
这节课我们来看一看相似三角形性质的一些实际应用.
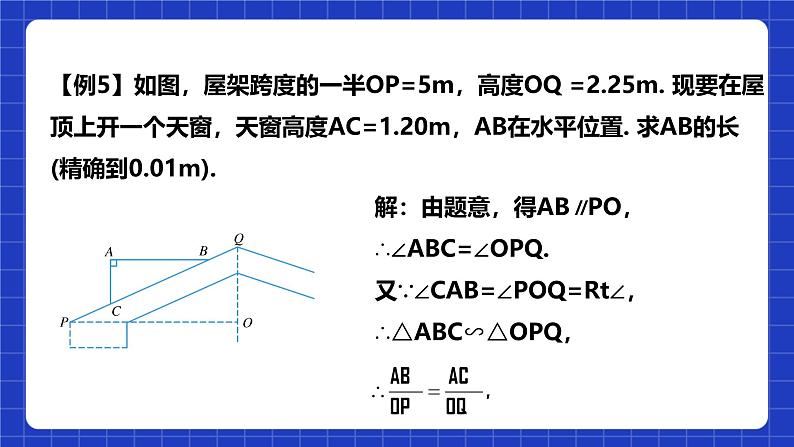
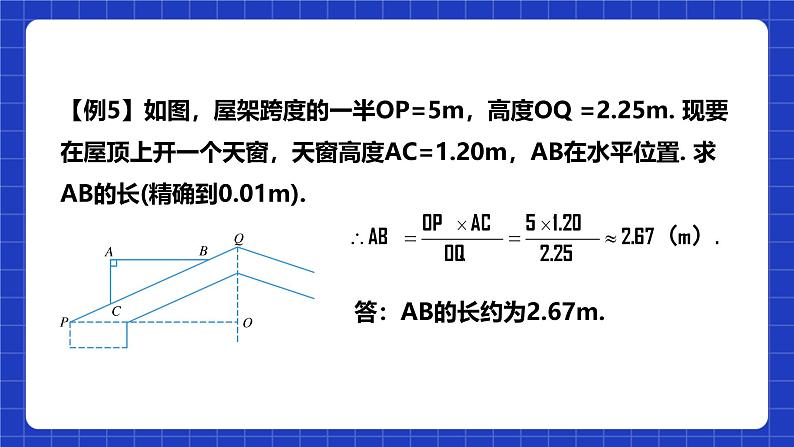
【例5】如图，屋架跨度的一半OP=5m，高度OQ =2.25m. 现要在屋顶上开一个天窗，天窗高度AC=1.20m，AB在水平位置. 求AB的长(精确到0.01m).
分析：若物体的高度和宽度不能被直接测量，则一般思路是根据题意和所求，建立相关的相似三角形的模型，然后根据相似三角形的性质以及比例关系可求得.
解：由题意，得AB∥PO，∴∠ABC=∠OPQ.又∵∠CAB=∠POQ=Rt∠，∴△ABC∽△OPQ，
答：AB的长约为2.67m.
【总结归纳】若物体的高度(或宽度)不能被直接测量，则一般思路是根据题意和所求，建立相关的相似三角形的模型，然后根据相似三角形的性质以及比例关系求得．
一般步骤：1. 构造相似三角形；2. 找出比例式；3. 代入数据 ；4. 计算求解.
分析：解决此类问题，可以先构造△CDE和△ABE，然后证明这两个三角形相似，找出比例线段，带入求值即可.
【例6】数学兴趣小组测校园内一棵树高，有以下两种方法：方法一：如图，镜子放在离树(AB)8m的点E处，然后沿着直线BE 后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.8m，观察者目高CD=1.6m.求树高AB（精确到0.1m）.
解：由题意，得△CDE和△ABE，作EF⊥BD，∵∠CEF=∠AEF，∴∠CED=∠AEB.又∵∠CDE=∠ABE=Rt∠，∴△CDE∽△ABE，
答：树高AB的长约为4.6m.
方法二：如图，把长为2.40m的标杆CD直立在地面上，量出树的影长为2.80m，标杆的影长为1.47m.求树高AB（精确到0.1m）.
解：由题意，得AE∥CF，∴∠AEB=∠CFD,又∵∠ABE=∠CDF=90°，∴△ABE∽△CDF，
【总结归纳】利用相似三角形测量高度.
测高方法一：测量不能到达顶部的物体的高度，可以用“在同一时刻物高与影长成正比例”的原理解决。 测高方法二：测量不能到达顶部的物体的高度，也可以用“利用镜子的反射测量高度”的原理解决。
【知识技能类作业】 必做题：1.如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度，已知标杆BE高1.5 m，测得AB＝1.2 m，BC＝12.8 m，则建筑物CD的高是(　　)A．17.5 m 　B．17 m 　C．16.5 m 　D．15 m
2.如图，为测量楼高AB，在适当位置竖直放置一根高2 m的标杆MN，并在同一时刻测得它们落在地面上的影长AC＝20 m，MP＝2.5 m，则楼高AB为(　　).A．15 m B．16 m C．18 m D．20 m
3.如图，树AB在路灯O的照射下形成投影AC，已知路灯高PO＝5 m，树影AC＝3 m，树AB与路灯O的水平距离AP＝4.5 m，则树的高度AB为(　　).A . 2 m B . 3 mC . 5mD . 4.5m
4.如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2∶5，且三角板的一边长为8 cm，则投影三角板的对应边长为(　　)A．20 cm B．10 cm C．8 cm D．3.2 cm
【知识技能类作业】 选做题：5.《九章算术》中记载：“今有邑方不知大小，各开中门，出北门四十步有木，出西门八百一十步见木，问：邑方几何？”译文：如图，一座正方形城池，北门、西门正中A，C处各开一道门，从点A往正北方向走40步刚好有一棵树位于点B处，若从点C往正西方向走810步到达点D处时正好看到此树，则正方形城池的边长为(　　).A．360步　B．270步　C．180步　D．90步
6.图1是装了液体的高脚杯示意图(数据如图)，用去一部分液体后如图2所示，此时液面AB＝(　　).A．1 cm B．2 cm C．3 cm D．4 cm
7.小明和小王同学一起合作来测量某建筑物顶部旗杆的高，如图所示，在某一时刻，他们在阳光下，分别测得该建筑物OB的影长OC为16米，OA的影长OD为20米，小明的影长FG为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且AO⊥OD，EF⊥FG，已知小明的身高EF为1.8米，求旗杆AB的长度。
本节课你学到了哪些知识？
1.相似三角形的应用主要有如下两个方面：(1)利用相似三角形测量高度，(2)利用相似三角形测量宽度.2.测高的方法：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长的比例”的原理解决．3.测距的方法：测量不能达到两点间的距离，常构造相似三角形求解．
【知识技能类作业】必做题
1.如图，数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度，他们通过调整测量位置，使边AC与旗杆顶点M在同一直线上，已知AC＝0.8米，BC＝0.5米，目测点A到地面的距离AD＝1.5米，到旗杆的水平距离AE＝20米，则旗杆MN的高度为(　　).A．12米 B．12.5米 C．14米 D．15米
2.如图，小明为了测量树的高度CD，他在B处放置一块平面镜，然后他站在A处刚好能从镜中看到树顶D，已知A、B、C三点在同一水平面上，且AB＝2 m，BC＝8 m．他的眼睛离地面的高度AE为1.6 m，则树的高度CD为________m.
选做题：3.如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时，她测得一根长为1 m的竹竿的影长是0.8 m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，她先测得留在墙壁上的影高为1.2 m，又测得地面上的影长为2.6 m，请你帮她算一下，树高是(　　).A．3.25 m B．4.25 m C．4.45 m D．4.75 m
【综合实践类作业】4.如图①，在Rt△AEF内部作一个矩形ABCD，其中AB和AD分别在两直角边上，AF＝40m，AE＝30m.如果设矩形的一边AB＝25m，则AD的长度是多少？