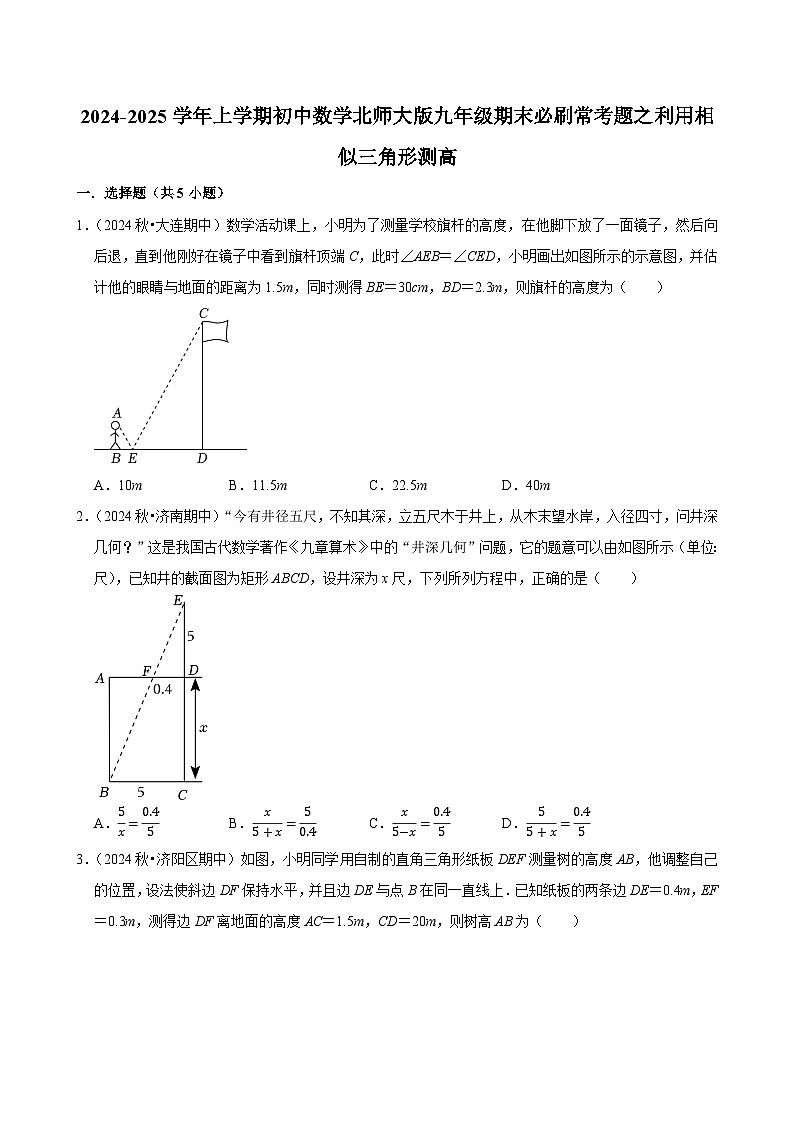
2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之利用相似三角形测高练习

这是一份2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之利用相似三角形测高练习，共20页。

A．10mB．11.5mC．22.5mD．40m
2．（2024秋•济南期中）“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学著作《九章算术》中的“井深几何”问题，它的题意可以由如图所示（单位：尺），已知井的截面图为矩形ABCD，设井深为x尺，下列所列方程中，正确的是（ ）
A．5x=0.45B．x5+x=50.4C．x5−x=0.45D．55+x=0.45
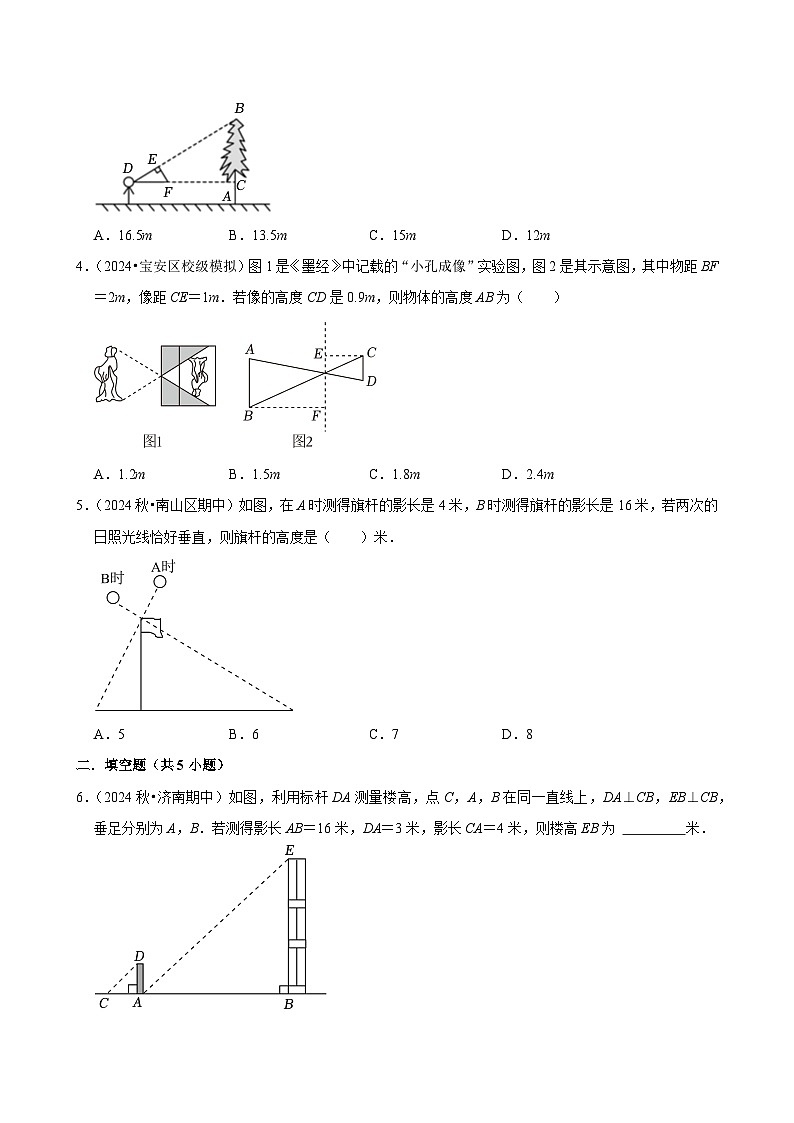
3．（2024秋•济阳区期中）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DE＝0.4m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为（ ）
A．16.5mB．13.5mC．15mD．12m
4．（2024•宝安区校级模拟）图1是《墨经》中记载的“小孔成像”实验图，图2是其示意图，其中物距BF＝2m，像距CE＝1m．若像的高度CD是0.9m，则物体的高度AB为（ ）
A．1.2mB．1.5mC．1.8mD．2.4m
5．（2024秋•南山区期中）如图，在A时测得旗杆的影长是4米，B时测得旗杆的影长是16米，若两次的日照光线恰好垂直，则旗杆的高度是（ ）米．
A．5B．6C．7D．8
二．填空题（共5小题）
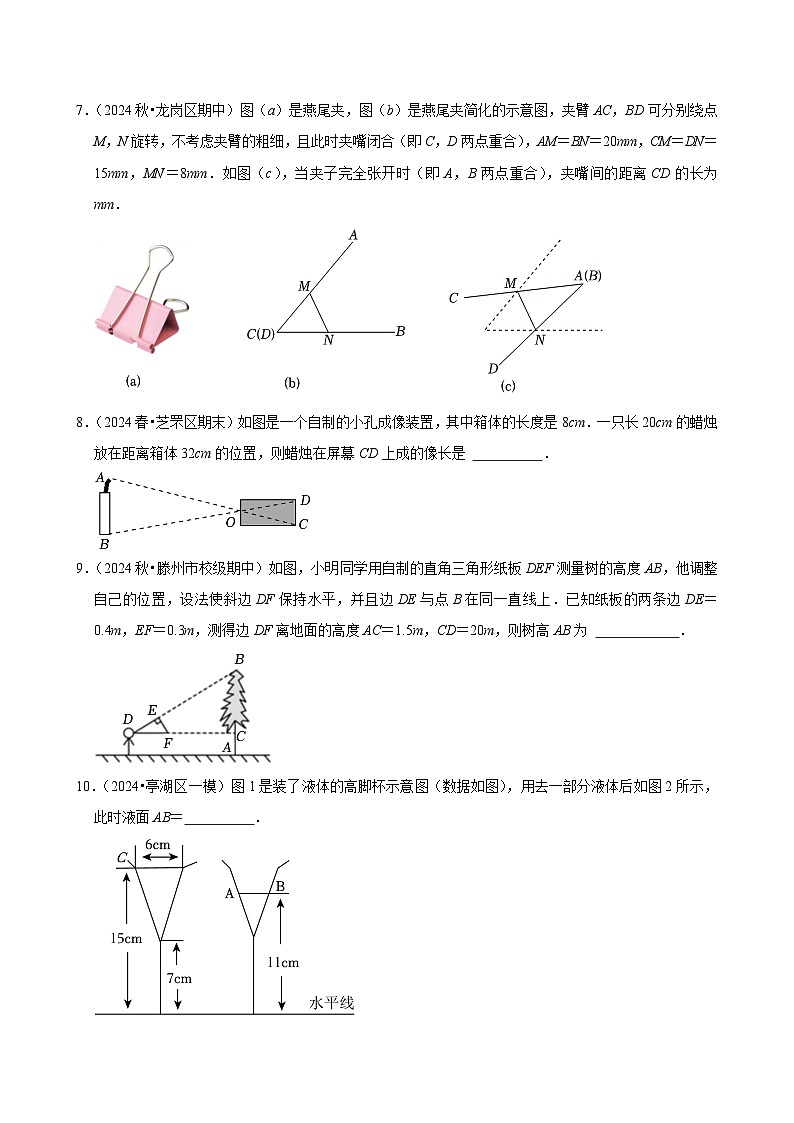
6．（2024秋•济南期中）如图，利用标杆DA测量楼高，点C，A，B在同一直线上，DA⊥CB，EB⊥CB，垂足分别为A，B．若测得影长AB＝16米，DA＝3米，影长CA＝4米，则楼高EB为 米．
7．（2024秋•龙岗区期中）图（a）是燕尾夹，图（b）是燕尾夹简化的示意图，夹臂AC，BD可分别绕点M，N旋转，不考虑夹臂的粗细，且此时夹嘴闭合（即C，D两点重合），AM＝BN＝20mm，CM＝DN＝15mm，MN＝8mm．如图（c），当夹子完全张开时（即A，B两点重合），夹嘴间的距离CD的长为 mm．
8．（2024春•芝罘区期末）如图是一个自制的小孔成像装置，其中箱体的长度是8cm．一只长20cm的蜡烛放在距离箱体32cm的位置，则蜡烛在屏幕CD上成的像长是 ．
9．（2024秋•滕州市校级期中）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DE＝0.4m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为 ．
10．（2024•亭湖区一模）图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB＝ ．
三．解答题（共5小题）
11．（2024秋•泰兴市期中）如图，在△ABC中，AB＝6，AC＝10，点D是AB的中点．请用无刻度直尺和圆规在AC边上作出点E，使△ADE∽△ACB，并求AE的长．
12．（2024秋•西安期中）如图，在数学实践活动课上，小辰准备测量一座电视塔的高度．他站在该电视塔的影子上前后移动，直到他自己影子的顶端正好与电视塔的影子的顶端重合（点E处），此时他与该塔的距离BD＝22m．已知电视塔、小辰均与地面BE垂直，且小辰的身高CD＝1.7m，他的影长DE＝2m．求该电视塔的高度（AB）．
13．（2024秋•合浦县期中）为了测量水平地面上一棵不可攀的树的高度，某学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在与树底端B相距8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝2米，观察者目高CD＝1.5米，求树AB的高度．
14．（2024•石家庄模拟）为测量操场上悬挂国旗的旗杆的高度，设计的测量方案如图所示：标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，E，C，A三点共线，求旗杆AB的高度．
15．（2024秋•昌平区期中）如图，小明欲测量一座信号发射塔的高度．他站在该塔的影子上前后移动，直到他自己影子的顶端正好与塔的影子的顶端重合，此时他与该塔的距离CE＝20米．已知小明的身高DE为1.8米，他的影长AE为2米．求信号发射塔的高度BC．
2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之利用相似三角形测高
参考答案与试题解析
一．选择题（共5小题）
1．（2024秋•大连期中）数学活动课上，小明为了测量学校旗杆的高度，在他脚下放了一面镜子，然后向后退，直到他刚好在镜子中看到旗杆顶端C，此时∠AEB＝∠CED，小明画出如图所示的示意图，并估计他的眼睛与地面的距离为1.5m，同时测得BE＝30cm，BD＝2.3m，则旗杆的高度为（ ）
A．10mB．11.5mC．22.5mD．40m
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】A
【分析】根据镜面反射性质，可求出∠AEB＝∠CED，再利用垂直求∠ABE＝∠CDE＝90°，得出△AEB∽△CED，最后根据三角形相似的性质，即可求出答案．
【解答】解：由题意得，AB＝1.5m，BE＝0.3m，
根据镜面反射可知：∠AEB＝∠CED，
∵AB⊥BD，DE⊥BD，
∴∠ABE＝∠CDE＝90°，
∴△AEB∽△CED，
∴ABCD=BEED，
∵BD＝2.3m，
∴ED＝2m，
∴1.5CD=0.32，
解得CD＝10，
则旗杆的高度为10米．
故选：A．
【点评】本题考查了相似三角形的应用，解题的关键在于熟练掌握镜面反射的基本性质和相似三角形的性质．
2．（2024秋•济南期中）“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学著作《九章算术》中的“井深几何”问题，它的题意可以由如图所示（单位：尺），已知井的截面图为矩形ABCD，设井深为x尺，下列所列方程中，正确的是（ ）
A．5x=0.45B．x5+x=50.4C．x5−x=0.45D．55+x=0.45
【考点】相似三角形的应用；由实际问题抽象出分式方程．
【答案】D
【分析】根据题意可证明△EFD∽△EBC得到EDEC=DFBC，然后代入数值即可得到答案．
【解答】解：如图，
∵DF∥BC，
∴△EFD∽△EBC，
∴EDEC=DFBC，
∵DF＝0.4，BC＝5，DE＝5，CD＝x，
∴55+x=0.45，
故选：D．
【点评】本题主要考查了相似三角形的应用举例，证明△EFD∽△EBC是解题的关键．
3．（2024秋•济阳区期中）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DE＝0.4m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为（ ）
A．16.5mB．13.5mC．15mD．12m
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】A
【分析】利用Rt△DEF和Rt△BCD相似求得BC的长后加上边DF到地面的高度AC，即可求得树高AB．
【解答】解：∵∠DEF＝∠DCB＝90°，∠D＝∠D，
∴△DEF∽△DCB，
∴DEDC=EFCB，
∵DE＝0.4m，EF＝0.3m，CD＝20m，
∴0.420=0.3BC，
∴CB＝15m，
∴AB＝AC+BC＝1.5+15＝16.5（m）．
故选：A．
【点评】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．
4．（2024•宝安区校级模拟）图1是《墨经》中记载的“小孔成像”实验图，图2是其示意图，其中物距BF＝2m，像距CE＝1m．若像的高度CD是0.9m，则物体的高度AB为（ ）
A．1.2mB．1.5mC．1.8mD．2.4m
【考点】相似三角形的应用．
【专题】图形的相似；推理能力．
【答案】C
【分析】由相似三角形对应高的比等于相似比，得到AB：DC＝BF：CE，代入有关数据即可求出AB＝1.8m．
【解答】解：∵△OAB∽△ODC，
∴AB：DC＝BF：CE，
∵CD＝0.9m，BF＝2m，CE＝1m，
∴AB：0.9＝2：1，
∴AB＝1.8m，
故选：C．
【点评】本题考查相似三角形的应用，关键是掌握相似三角形的性质：相似三角形对应高的比等于相似比．
5．（2024秋•南山区期中）如图，在A时测得旗杆的影长是4米，B时测得旗杆的影长是16米，若两次的日照光线恰好垂直，则旗杆的高度是（ ）米．
A．5B．6C．7D．8
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】D
【分析】利用等角的余角相等得到∠QPC＝∠D，则可判断Rt△PCQ∽Rt△DPQ，然后利用相似比可计算出PQ．
【解答】解：如图，∠CPD＝90°，QC＝4m，QD＝16m，
∵PQ⊥CD，
∴∠PQC＝90°，
∴∠C+∠QPC＝90°，
而∠C+∠D＝90°，
∴∠QPC＝∠D，
∴Rt△PCQ∽Rt△DPQ，
∴PQQD=QCPQ，
即PQ16=4PQ，
∴PQ＝8，
即旗杆的高度为8m．
故选：D．
【点评】本题主要考查了相似三角形的应用，解答本题的关键是熟练掌握相似三角形的性质．
二．填空题（共5小题）
6．（2024秋•济南期中）如图，利用标杆DA测量楼高，点C，A，B在同一直线上，DA⊥CB，EB⊥CB，垂足分别为A，B．若测得影长AB＝16米，DA＝3米，影长CA＝4米，则楼高EB为 12 米．
【考点】相似三角形的应用．
【专题】图形的相似；运算能力．
【答案】12．
【分析】根据垂直定义可得∠DAC＝∠EBA＝90°，再利用平行线的性质可得∠DCA＝∠EAB，从而可得△DCA∽△EAB，然后利用相似三角形的性质进行计算即可解答．
【解答】解：∵DA⊥CB，EB⊥CB，
∴∠DAC＝∠EBA＝90°，
∵DC∥EA，
∴∠DCA＝∠EAB，
∴△DCA∽△EAB，
∴DAEB=ACAB，
∴3EB=416，
解得：EB＝12，
∴楼高EB为12米，
故答案为：12．
【点评】本题考查了相似三角形的应用，熟练掌握相似三角形的判定与性质是解题的关键．
7．（2024秋•龙岗区期中）图（a）是燕尾夹，图（b）是燕尾夹简化的示意图，夹臂AC，BD可分别绕点M，N旋转，不考虑夹臂的粗细，且此时夹嘴闭合（即C，D两点重合），AM＝BN＝20mm，CM＝DN＝15mm，MN＝8mm．如图（c），当夹子完全张开时（即A，B两点重合），夹嘴间的距离CD的长为 14 mm．
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】14．
【分析】连接CD，根据已知可证△AMN∽△ACD，然后利用相似三角形的性质，进行计算即可解答．
【解答】解：连接CD，如图，
∵AM＝BN＝20mm，CM＝DN＝15mm，MN＝8mm，
∴AMAC=ANAD=47，
又∵∠A＝∠A，
∴△AMN∽△ACD，
∴MNCD=47，
∴CD=MN47=14（mm），
∴夹嘴间的距离CD为14mm；
故答案为：14．
【点评】本题考查了相似三角形的应用，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
8．（2024春•芝罘区期末）如图是一个自制的小孔成像装置，其中箱体的长度是8cm．一只长20cm的蜡烛放在距离箱体32cm的位置，则蜡烛在屏幕CD上成的像长是 5cm ．
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】5cm．
【分析】先根据题意，通过作辅助线构造相似三角形，再利用三角形相似的性质得到相似比，然后根据比例性质计算．
【解答】解：如图，过点O作EF⊥AB于E，EF⊥CD于F，
根据题意知：AB＝20cm，OF＝8cm，OE＝32cm，
∵AB∥CD，
∴△OAB∽△ODC，
∴ABCD=OEOF，即20CD=328，
∴CD＝5cm．
故答案为：5cm．
【点评】本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
9．（2024秋•滕州市校级期中）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DE＝0.4m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为 16.5m ．
【考点】相似三角形的应用．
【专题】图形的相似；运算能力．
【答案】16.5m．
【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB．
【解答】解：∵∠DEF＝∠BCD＝90°，∠D＝∠D，
∴△DEF∽△DCB，
∴BCEF=DCDE，
∵DE＝0.4m，EF＝0.3m，AC＝1.5m，CD＝20m，
∴BC0.3=200.4，
∴BC＝15（m），
∴AB＝AC+BC＝1.5+15＝16.5（m）．
故答案为：16.5m．
【点评】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．
10．（2024•亭湖区一模）图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB＝ 3cm ．
【考点】相似三角形的应用．
【专题】图形的相似；推理能力．
【答案】3cm．
【分析】高脚杯前后的两个三角形相似．根据相似三角形的判定和性质即可得出结果．
【解答】解：如图：过O作OM⊥CD，垂足为M，过O作ON⊥AB，垂足为N，
∵CD∥AB，
∴△CDO∽ABO，即相似比为CDAB，
∴CDAB=OMON，
∵OM＝15﹣7＝8（cm），ON＝11﹣7＝4（cm），
∴6AB=84，
∴AB＝3cm，
故答案为：3cm．
【点评】本题考查相似三角形的应用，解本题的关键熟练掌握相似三角形的判定与性质．
三．解答题（共5小题）
11．（2024秋•泰兴市期中）如图，在△ABC中，AB＝6，AC＝10，点D是AB的中点．请用无刻度直尺和圆规在AC边上作出点E，使△ADE∽△ACB，并求AE的长．
【考点】作图﹣相似变换．
【专题】图形的相似；尺规作图；几何直观；推理能力．
【答案】作图见解析，AE＝1.8．
【分析】以C为圆心，DA为半径作弧与CB，CA相交，两交点确定线段a，以D为圆心，DA为半径作弧，以A为圆心，线段a为半径作弧，两弧交于一点，连接点D与交点并延长与CA相交，即为点E；由△ADE∽△ACB得到ADAC=AEAB，代入数据即可求解AE．
【解答】解：作图如下；
∵△ADE∽△ACB，
∴ADAC=AEAB，
∵AB＝6，AC＝10，点D是AB的中点，
∴AD＝3，
∴310=AE6，
解得：AE＝1.8．
【点评】本题考查了作图﹣相似变换，熟练掌握作一个角等于已知角的方法是解答本题的关键．
12．（2024秋•西安期中）如图，在数学实践活动课上，小辰准备测量一座电视塔的高度．他站在该电视塔的影子上前后移动，直到他自己影子的顶端正好与电视塔的影子的顶端重合（点E处），此时他与该塔的距离BD＝22m．已知电视塔、小辰均与地面BE垂直，且小辰的身高CD＝1.7m，他的影长DE＝2m．求该电视塔的高度（AB）．
【考点】相似三角形的应用．
【专题】图形的相似；推理能力．
【答案】20.4m．
【分析】利用相似三角形的判定与性质求解即可．
【解答】解：∵AB⊥BE，CD⊥BE，
∴AB∥CD，
∴△ABE∽△CDE，
∴ABCD=BEDE，
∴ABCD=DE+BDDE，
∴AB1.7=2+222，
∴AB＝20.4（m）．
【点评】本题考查了相似三角形应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
13．（2024秋•合浦县期中）为了测量水平地面上一棵不可攀的树的高度，某学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在与树底端B相距8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝2米，观察者目高CD＝1.5米，求树AB的高度．
【考点】相似三角形的应用．
【专题】图形的相似；应用意识．
【答案】6米．
【分析】根据镜面反射的性质求出△ABE∽△CDE，再根据其相似比解答．
【解答】解：根据题意得∠CDE＝∠ABE＝90°，∠CED＝∠AEB，
∴△ABE∽△CDE，
∴BEDE=ABCD，
∵BE＝8，CD＝1.5，DE＝2，
∴82=AB1.5，
解得AB＝6，
答：树AB的高度为6米．
【点评】此题考查相似三角形的应用，应用反射的基本性质，得出三角形相似，运用相似比是解题的关键．
14．（2024•石家庄模拟）为测量操场上悬挂国旗的旗杆的高度，设计的测量方案如图所示：标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，E，C，A三点共线，求旗杆AB的高度．
【考点】相似三角形的应用．
【专题】图形的相似；运算能力；推理能力；应用意识．
【答案】13.5m．
【分析】利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB＝EF＝1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出CGAH=EGEH，把相关条件代入即可求得AH＝11.9，于是得到结论．
【解答】解：过E作EH⊥AB于H，交CD于G，
∵CD⊥FB，AB⊥FB，
则四边形EFDG和四边形BHGD是矩形，
∴CD∥AB，EF＝GD＝HB，EG＝FD，EH＝FB，
∴△CGE∽△AHE，
∴CGAH=EGEH，
即：CD−EFAH=FDFD+BD，
∴3−1.6AH=22+15，
∴AH＝11.9，
∴AB＝AH+HB＝AH+EF＝11.9+1.6＝13.5（m）．
答：旗杆AB的高度为13.5m．
【点评】本题考查了相似三角形的应用，主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．
15．（2024秋•昌平区期中）如图，小明欲测量一座信号发射塔的高度．他站在该塔的影子上前后移动，直到他自己影子的顶端正好与塔的影子的顶端重合，此时他与该塔的距离CE＝20米．已知小明的身高DE为1.8米，他的影长AE为2米．求信号发射塔的高度BC．
【考点】相似三角形的应用．
【专题】图形的相似；推理能力．
【答案】见试题解答内容
【分析】先证明△ABC△∽ADE，利用三角形相似的性质即可求解．
【解答】解：∵BC⊥AC，DE⊥AC，
∴DE∥BC，
∴△ABC△∽ADE，
∴DEBC=AEAC，
∵CE＝20，DE＝1.8，AE＝2，
∴AC＝CE+AE＝22，
∴1.8BC=222，
∴BC＝19.8（米），
∴信号发射塔的高度为19.8米．
【点评】本题考查了相似三角形在测量高度时的应用，证明△ABC△∽ADE是解题的关键．
考点卡片
1．由实际问题抽象出分式方程
由实际问题抽象出分式方程的关键是分析题意找出相等关系．
（1）在确定相等关系时，一是要理解一些常用的数量关系和一些基本做法，如行程问题中的相遇问题和追击问题，最重要的是相遇的时间相等、追击的时间相等．
（2）列分式方程解应用题要多思、细想、深思，寻求多种解法思路．
2．相似三角形的应用
（1）利用影长测量物体的高度．①测量原理：测量不能到达顶部的物体的高度，通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决．②测量方法：在同一时刻测量出参照物和被测量物体的影长来，再计算出被测量物的长度．
（2）利用相似测量河的宽度（测量距离）．①测量原理：测量不能直接到达的两点间的距离，常常构造“A”型或“X”型相似图，三点应在一条直线上．必须保证在一条直线上，为了使问题简便，尽量构造直角三角形．②测量方法：通过测量便于测量的线段，利用三角形相似，对应边成比例可求出河的宽度．
（3）借助标杆或直尺测量物体的高度．利用杆或直尺测量物体的高度就是利用杆或直尺的高（长）作为三角形的边，利用视点和盲区的知识构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．
3．作图-相似变换
（1）两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到．
（2）相似图形的作图在没有明确规定的情况下，我们可以利用相似的基本图形“A”型和“X”型进行简单的相似变换作图．如图所示：
（3）如果题目有条件限制，可根据相似三角形的判定条件作为作图的依据．比较简单的是把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形．