沪教版数学九年级上册期末复习训练重难点01 相似三角形（5种模型）（2份，原卷版+解析版）

这是一份沪教版数学九年级上册期末复习训练重难点01 相似三角形（5种模型）（2份，原卷版+解析版），文件包含沪教版数学九年级上册期末复习训练重难点01相似三角形5种模型原卷版doc、沪教版数学九年级上册期末复习训练重难点01相似三角形5种模型解析版doc等2份试卷配套教学资源，其中试卷共66页， 欢迎下载使用。
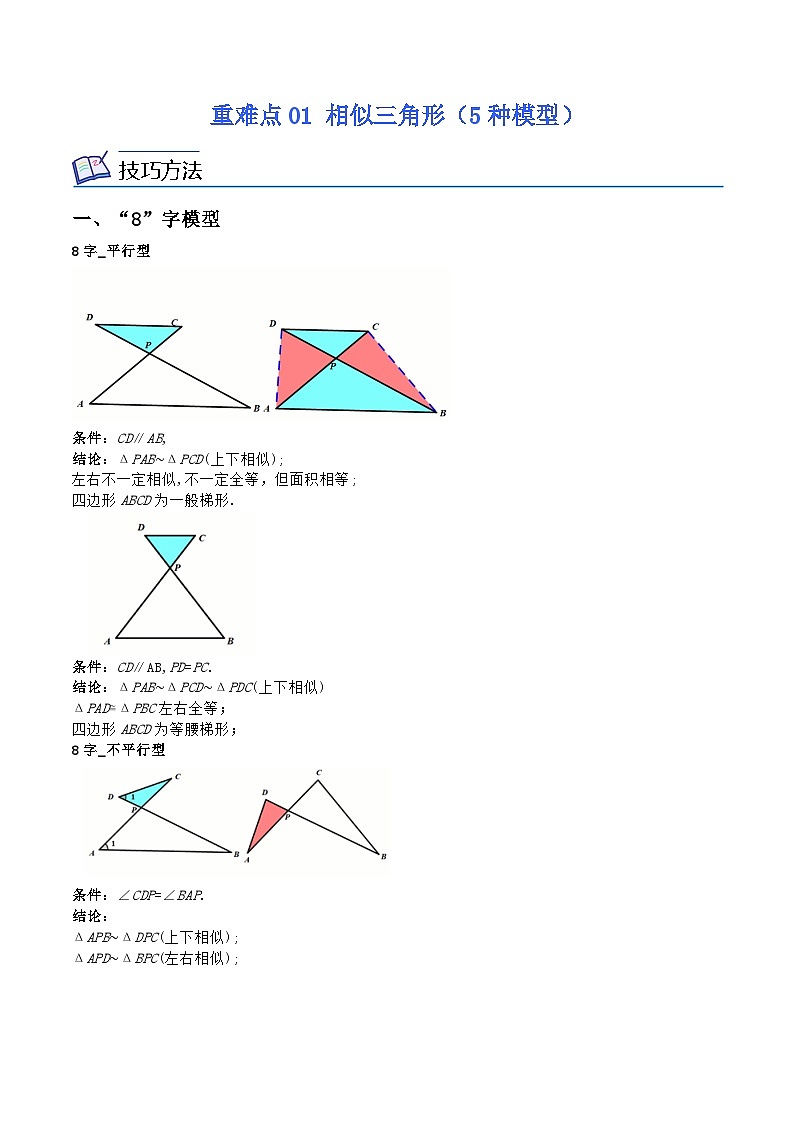
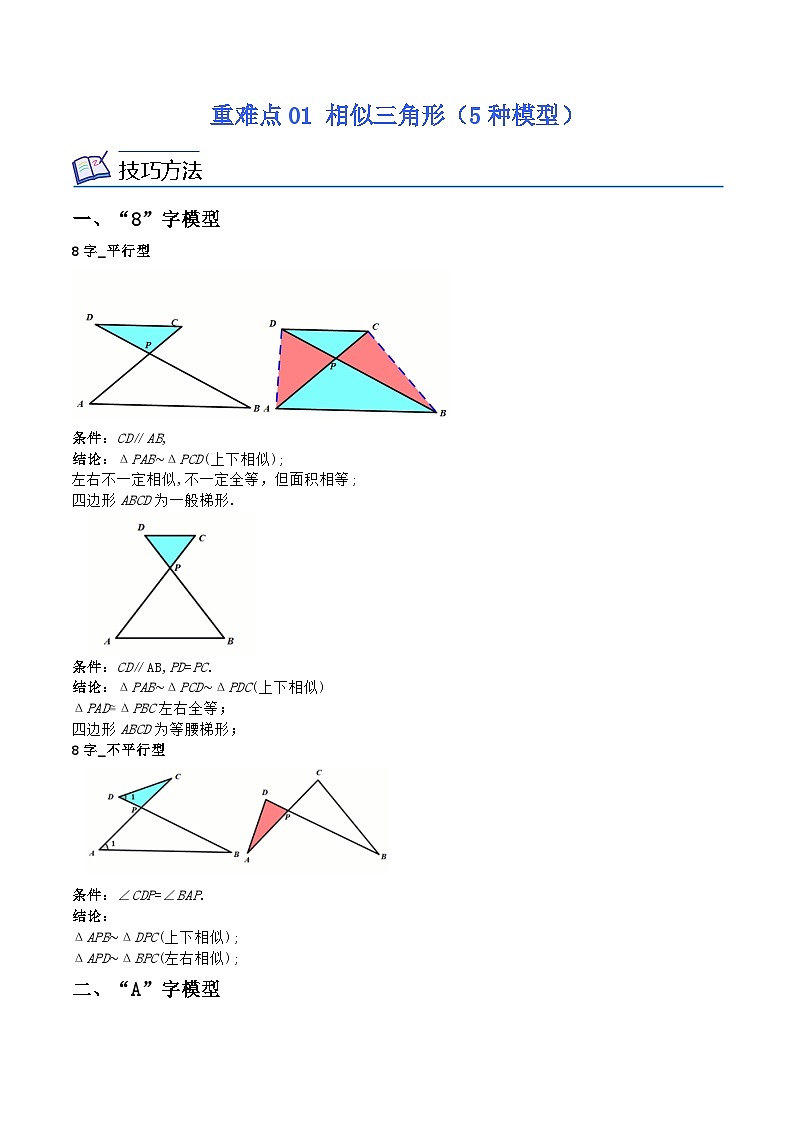
一、“8”字模型
8字_平行型
条件：CD∥AB,
结论：ΔPAB∼ΔPCD(上下相似);
左右不一定相似,不一定全等，但面积相等;
四边形ABCD为一般梯形.
条件：CD∥AB,PD=PC.
结论：ΔPAB∼ΔPCD∼ΔPDC(上下相似)
ΔPAD≅ΔPBC左右全等；
四边形ABCD为等腰梯形；
8字_不平行型
条件：∠CDP=∠BAP.
结论：
ΔAPB∼ΔDPC(上下相似);
ΔAPD∼ΔBPC(左右相似);
二、“A”字模型
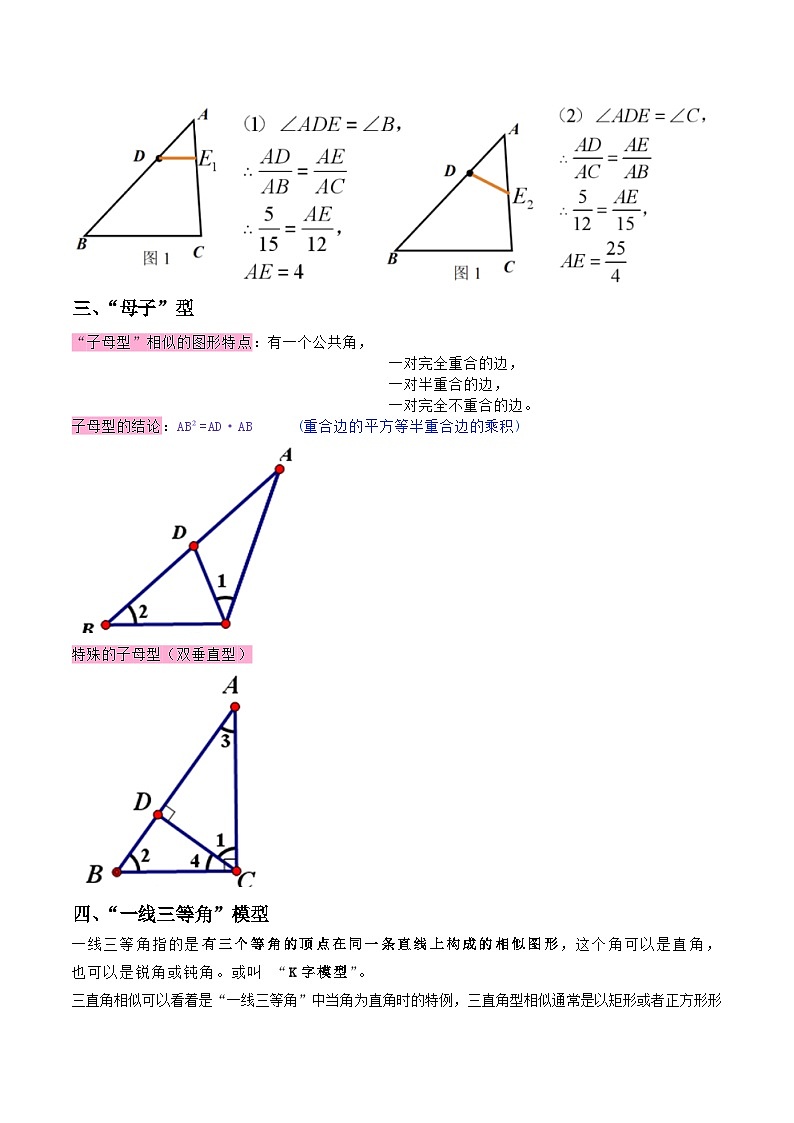
三、“母子”型
“子母型”相似的图形特点：有一个公共角，
一对完全重合的边，
一对半重合的边，
一对完全不重合的边。
子母型的结论：AB²=AD·AB (重合边的平方等半重合边的乘积)

特殊的子母型（双垂直型）
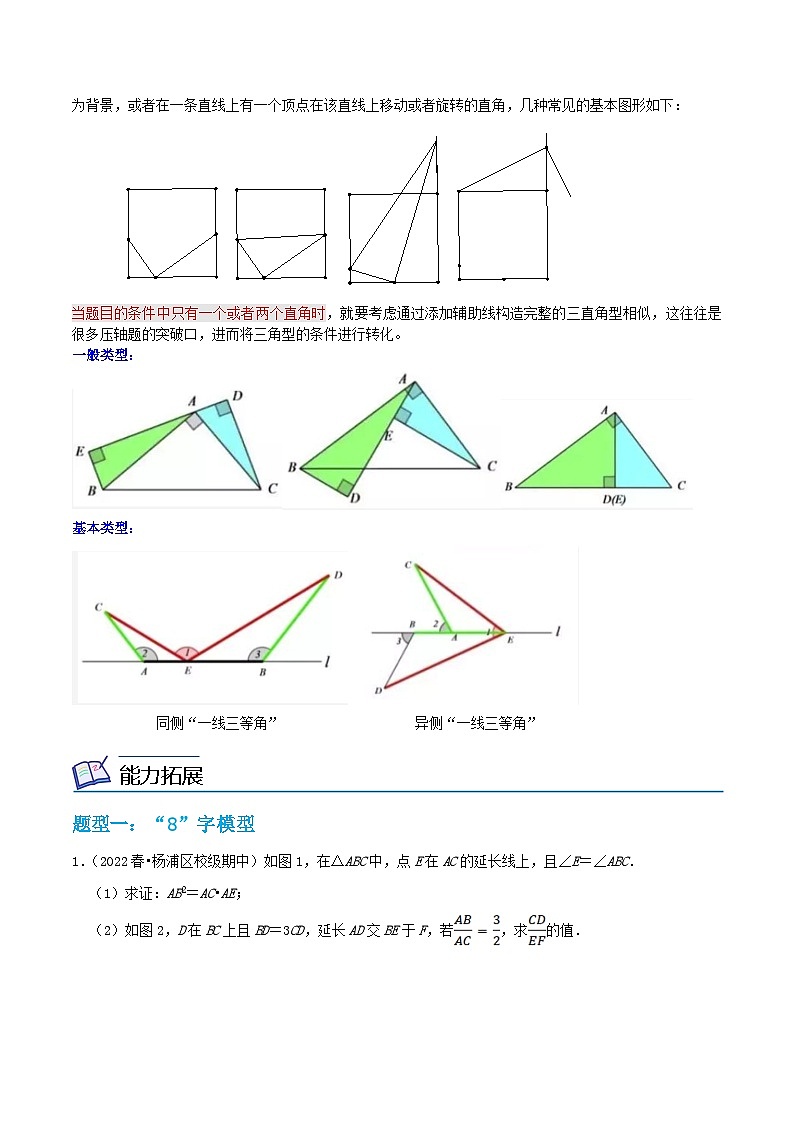
四、“一线三等角”模型
一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。或叫 “K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：
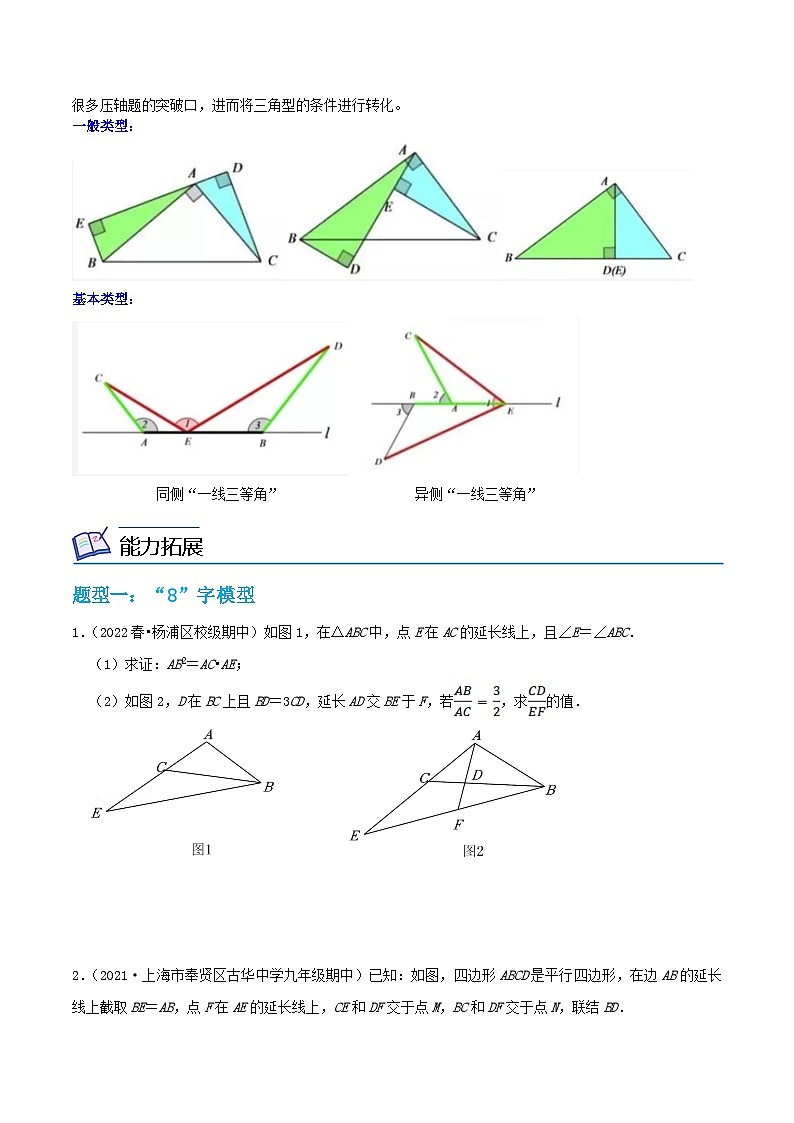
当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。
一般类型：
基本类型：
同侧“一线三等角” 异侧“一线三等角”
能力拓展
题型一：“8”字模型
1．（2022春•杨浦区校级期中）如图1，在△ABC中，点E在AC的延长线上，且∠E＝∠ABC．
（1）求证：AB2＝AC•AE；
（2）如图2，D在BC上且BD＝3CD，延长AD交BE于F，若，求的值．
【分析】（1）利用两角相等的两个三角形相似，证明△ABC∽△AEB，然后利用相似三角形的性质即可解答；
（2）过点E作EH∥CB，交AF的延长线于点H，利用（1）的结论可得，先AC＝2a，AB＝3a，从而求出AE的长，进而求出的值，再根据已知设CD＝m，BD＝3m，从而求出BC，BE的长，然后证明A字模型相似三角形△ACD∽△AEH，利用相似三角形的性质可得EHm，再证明8字模型相似三角形△BDF∽△EHF，利用相似三角形的性质可得，从而求出EF的长，进行计算即可解答．
【解答】（1）证明：∵∠E＝∠ABC，∠A＝∠A，
∴△ABC∽△AEB，
∴，
∴AB2＝AC•AE；
（2）解：过点E作EH∥CB，交AF的延长线于点H，
∵△ABC∽△AEB，
∴，
∴设AC＝2a，AB＝3a，
∴，
∴AEa，
∴，
∵BD＝3CD，
∴设CD＝m，则BD＝3m，
∴BC＝CD+BD＝4m，
∴，
∴EB＝6m，
∵EH∥CD，
∴∠ACD＝∠AEH，∠ADC＝∠AHE，
∴△ACD∽△AEH，
∴，
∴EHm，
∵EH∥BD，
∴∠BDF＝∠DHE，∠DBF＝∠FEH，
∴△BDF∽△EHF，
∴，
∴EFBEm，
∴，
∴的值为．
【点评】本题考查了相似三角形的判定与性质，平行线分线段成比例，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
2．（2021·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．
（1）求证：△BND∽△CNM；
（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．
【分析】（1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；
（2）先利用AD2=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=∠4，∠2=∠3，所以∠3=∠4，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．
【详解】证明：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
而BE=AB，
∴BE=CD，
而BE∥CD，
∴四边形BECD为平行四边形，
∴BD∥CE，
∵CM∥DB，
∴△BND∽△CNM；
（2）∵AD2=AB•AF，
∴AD：AB=AF：AD，
而∠DAB=∠FAD，
∴△ADB∽△AFD，
∴∠1=∠F，
∵CD∥AF，BD∥CE，
∴∠F=∠4，∠2=∠3，
∴∠3=∠4，
而∠NMC=∠CMD，
∴△MNC∽△MCD，
∴MC：MD=CN：CD，
∴MC•CD=MD•CN，
而CD=AB，
∴CM•AB=DM•CN．
【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．
3．（2021·上海·九年级期末）如图，在平行四边形ABCD中，BC=8，点E、F是对角线BD上的两点，且BE=EF=FD，AE的延长线交BC于点G，GF的延长线交AD于点H．
（1）求HD的长；
（2）设的面积为a，求四边形AEFH的面积．（用含a的代数式表示）
【答案】（1）2；（2）
【分析】（1）根据平行四边形的性质得，根据相似三角形的判定得，，由BE=EF=FD可得出，，根据相似三角形的性质即可求解；
（2）由BE=EF可得与的面积相等，根据相似三角形的面积比等于相似比的平方可得与的值，-即可得四边形AEFH的面积．
【详解】解：（1）∵平行四边形ABCD，BC=8，
∴，=8，
∴，，
∴，，
∵BE=EF=FD，
∴，，
∴BG=AD=4，HD=BG，
∴HD=2；
（2）∵BE=EF，
∴=a，
∴，
∵，，，，
∴，，
∴四边形AEFH的面积=-=．
【点睛】本题考查平行四边形的性质，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
4．（2020·上海奉贤·二模）已知：如图，在梯形ABCD中，CD∥AB，∠DAB＝90°，对角线AC、BD相交于点E，AC⊥BC，垂足为点C，且BC2＝CE•CA．
（1）求证：AD＝DE；
（2）过点D作AC的垂线，交AC于点F，求证：CE2＝AE•AF．
【分析】（1）根据相似三角形的判定定理得到△BCE∽△ACB，根据相似三角形的性质得到∠CBE＝∠CAB，根据等角的余角相等得到∠BEC＝∠DAE，根据等腰三角形的判定定理证明；
（2）根据平行线分线段成比例定理得到， ，得到，整理得到 CE2＝AE•EF，根据等腰三角形的三线合一得到AF＝EF，证明结论．
【详解】
证明：（1）∵BC2＝CE•CA，
∴，又∠ECB＝∠BCA，
∴△BCE∽△ACB，
∴∠CBE＝∠CAB，
∵AC⊥BC，∠DAB＝90°，
∴∠BEC+∠CBE＝90°，∠DAE+∠CAB＝90°，
∴∠BEC＝∠DAE，
∵∠BEC＝∠DEA，
∴∠DAE＝∠DEA，
∴AD＝DE；
（2）过点D作AC的垂线，交AC于点F，如图，
∵DF⊥AC，AC⊥BC，
∴∠DFE＝∠BCA＝90°，
∴DF∥BC，
∴，
∵DC∥AB，
∴，
∴，
∴CE2＝AE•EF，
∵AD＝DE，DF⊥AC，
∴AF＝EF，
∴CE2＝AE•AF．
【点睛】本题考查的是相似三角形的判定和性质、直角梯形的概念，掌握相似三角形的判定定理和性质定理是解题的关键．
题型二：“A”字模型
1．（2022春•浦东新区校级期中）一把梯子如图所示，其中四边形AKLB是梯形．已知AC＝CE＝EG＝GK，BD＝DF＝FH＝HL，AB＝0.5m，GH＝0.74m，求CD、EF的长．
【分析】先证明△ACD'∽△AGH'，找到CD'，再利用梯形CGHD的中位线等于两底和的一半，找到EF的值．
【解答】解：延长KA、LB交于点P，过A作AL'∥BL交CD、EF、GH、KL于点D'、F'、H'、L'，
∵AB∥KL，
∴．
又∵AC＝CE＝EG＝GK，BD＝DF＝FH＝HL，
∴，
∴．
∴AB∥CD．
同理得AB∥CD∥EF∥GH∥KL．
∴四边形AD'DB，D'F'FD，F'H'HF都为平行四边形边；
即AB＝D'D＝F'F＝H'H＝0.5m；GH＝0.74m，
∴GH'＝0.24m，
∵CD∥AH，
∴△ACD'∽△AGH'，
∴，AG＝3AC，
∴CD'GH'＝，
CD＝0.08+0.5＝0.58．
∵EF为梯形CGHD的中位线，
∴EF（CDtGH）＝0.66m．
【点评】本题考查了梯形CGHD的中位线平行于两底，并且等于两底和的一半，解题的关键是掌握相似的判定．
2．（2021秋•松江区期末）如图，已知△ABC中，∠ACB＝90°，AB＝6，BC＝4，D是边AB上一点（与点A、B不重合），DE平分∠CDB，交边BC于点E，EF⊥CD，垂足为点F．
（1）当DE⊥BC时，求DE的长；
（2）当△CEF与△ABC相似时，求∠CDE的正切值；
（3）如果△BDE的面积是△DEF面积的2倍，求这时AD的长．
【分析】（1）证明△DCE≌△DBE（ASA），可得CE＝BE＝2，根据tan∠B，即可求得答案；
（2）分两种情况：①当△CEF∽△ABC时，可证得∠CDB＝90°，再根据DE平分∠CDB，可得∠CDE＝45°，再由特殊角的三角函数值即可求得答案；②当△CEF∽△BAC时，则∠ECF＝∠ABC，得出DC＝DB，再由DE平分∠CDB，可得DE⊥BC，推出∠CDE＝∠BAC，利用三角函数定义即可求得答案；
（3）如图，过点E作EG⊥AB于点G，根据角平分线性质可得出EF＝EG，推出DF＝DG，再由△BDE的面积是△DEF面积的2倍，可得出BD＝2DF，进而推出DE＝BE，设BE＝x，则DE＝x，CE＝BC﹣BE＝4﹣x，BG＝BE•csBx，BD＝2BGx，DG＝DF＝BGx，AD＝AB﹣BD＝6x，根据△CDE∽CBD，得出，建立方程求解即可．
【解答】解：（1）在Rt△ABC中，∠ACB＝90°，AB＝6，BC＝4，
∴AC2，
∵DE平分∠CDB，
∴∠CDE＝∠BDE，
∵DE⊥BC，
∴∠DEC＝∠DEB＝90°，
在△DCE和△DBE中，
，
∴△DCE≌△DBE（ASA），
∴CE＝BE，
∵CE+BE＝BC＝4，
∴CE＝BE＝2，
∵tan∠B，
∴，
∴DE；
（2）∵EF⊥CD，
∴∠CFE＝90°＝∠ACB，
∵△CEF与△ABC相似，
∴△CEF∽△ABC或△CEF∽△BAC，
①当△CEF∽△ABC时，
则∠ECF＝∠BAC，
∵∠ACB＝90°，
∴∠BAC+∠ABC＝90°，
∴∠ECF+∠ABC＝90°，
∴∠CDB＝90°，
∵DE平分∠CDB，
∴∠CDE∠CDB90°＝45°，
∴tan∠CDE＝tan45°＝1；
②当△CEF∽△BAC时，
则∠ECF＝∠ABC，
∴DC＝DB，
∵DE平分∠CDB，
∴DE⊥BC，
∴∠CDE+∠ECF＝90°，
∵∠BAC+∠ABC＝90°，
∴∠CDE＝∠BAC，
∴tan∠CDE＝tan∠BAC，
综上所述，∠CDE的正切值为1或；
（3）如图，过点E作EG⊥AB于点G，
∵DE平分∠CDB，EF⊥CD，EG⊥AB，
∴EF＝EG，
∵DE＝DE，
∴Rt△DEF≌Rt△DEG（HL），
∴DF＝DG，
∵△BDE的面积是△DEF面积的2倍，
∴BD＝2DF，
∴DG＝BG，
∵EG⊥BD，
∴DE＝BE，
设BE＝x，则DE＝x，CE＝BC﹣BE＝4﹣x，BG＝BE•csBx，
∴BD＝2BGx，DG＝DF＝BGx，
∴AD＝AB﹣BD＝6x，
∵DE平分∠CDB，
∴∠CDE＝∠BDE，
∵DE＝BE，
∴∠BDE＝∠B，
∴∠CDE＝∠B，
∵∠DCE＝∠BCD，
∴△CDE∽CBD，
∴，即，
解得：CD＝3，x，
∴AD＝6x＝6，
故这时AD的长为．
【点评】本题是几何综合题，考查了直角三角形性质，勾股定理，全等三角形判定和性质，相似三角形的判定和性质，角平分线性质，三角形面积，三角函数等知识，解题关键是熟练掌握相似三角形的判定和性质等相关知识，运用分类讨论思想和方程思想解决问题．
3．（2021·上海市金山初级中学九年级期中）如图，在△ABC中，点D在边AB上，点E、点F在边AC上，且DEBC，．
（1）求证：DFBE；
（2）如且AF＝2，EF＝4，AB＝6．求证△ADE∽△AEB．
【分析】（1）由题意易得，则有，进而问题可求证；
（2）由（1）及题意可知，然后可得，进而可证，最后问题可求证．
【详解】解：（1）∵DEBC，
∴，
∵，
∴，
∴DFBE；
（2）∵AF＝2，EF＝4，
∴由（1）可知，，AE=6，
∵AB＝6，
∴，
∴，
∴，
∵∠A=∠A，
∴△ADE∽△AEB．
【点睛】本题主要考查相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键．
4．（2020·上海市徐汇中学九年级期中）已知：矩形ABCD中，AB＝9，AD＝6，点E在对角线AC上，且满足AE＝2EC，点F在线段CD上，作直线FE，交线段AB于点M，交直线BC于点N．
（1）当CF＝2时，求线段BN的长；
（2）若设CF＝x，△BNE的面积为y，求y关于x的函数解析式，并写出自变量的取值范围；
（3）试判断△BME能不能成为等腰三角形，若能，请直接写出x的值．
【答案】（1）BN＝10；（2），0＜x＜3；，3＜x＜4.5；（3）x＝2或或
【分析】（1）由得△CFE∽△AME，△NCF∽△NBM，进而求得；
（2）分为0＜x＜3和3＜x＜4.5两种情形，作EG⊥BC于G，根据三角形相似求出EG和BN；
（3）分为BM＝BE，EM＝BE，EN＝BM三种，可根据BM＝9﹣2CF求得．
【详解】解：（1）如图1，
在矩形ABCD中，BC＝AD＝6，，
∴△CFE∽△AME，△NCF∽△NBM，
∴,
∴AM＝2CF＝4，
∴BM＝AB﹣AM＝5，
∴，
∴BN＝10；
（2）当CF＝BM时，，此时△BEN不存在，
∴CF＝9﹣2CF，
∴CF＝3，
当点M和B点重合时，
AB＝2CF，
∴CF＝4.5，
∴分为0＜x＜3和3＜x＜4.5，
如图2，
当0＜x＜3时，
作EG⊥BC于G，
由（1）知，
EG＝3，AM＝2CF＝2x，
∴BM＝9﹣2x，
由得，，
∴，
∴y＝
＝
＝；
如图3，
当3＜x＜4.5时，
由得，

∴CN＝，
∴y＝
＝；
（3）如图4，
∵，
∴，
∴CG＝CB＝2，
∴GB＝CB﹣CG＝4，
∴BE＝5，
当BM＝BE＝5时，
9﹣2x＝5，
∴x＝2，
如图5，
当EM＝EB＝5时，
作EH⊥AB于H，
∴BM＝2BH＝2EG＝6，
∴9﹣2x＝6，
∴x=，
如图6，
当EM＝BM时，
作MH⊥BE于H，
在Rt△BMH中，BH＝，cs∠MBH＝cs∠BEG＝，
∴BM＝，
∴9﹣2x＝，
∴x＝，
综上所述：x＝2或或．
【点睛】此题考查相似三角形的判定及性质，锐角三角函数，勾股定理解直角三角形，矩形的性质，正确引出辅助线及掌握分类思想解决问题是解题的关键．
5．（2021·上海嘉定·二模）已知点P为线段AB上的一点，将线段AP绕点A逆时针旋转60°，得到线段AC；再将线段绕点B逆时针旋转120°，得到线段BD；点M是AD的中点，联结BM、CM．
（1）如图1，如果点P在线段CM上，求证：；
（2）如图1，如果点P在线段CM上，求证：；
（3）如果点P不在线段CM上（如图12），当点P在线段AB上运动时，的正切值是否发生变化？如果发生变化，简述理由；如果不发生变化，请求出的正切值．
【答案】（1）见解析；（2）见解析；（3）
【分析】（1）由旋转可得，△APC是等边三角形，∠PBD=120°，则∠BPM+∠PBD=180°，所以PM∥BD．
（2）利用三角形的中位线定理解决问题即可．
（3）延长BM至点G，使得MG=MB，连接AG，BC，GC，PC，可证△CBG是等边三角形且点M是BG的中点，可得结论．
【详解】解：（1）如图1中，
由题意可得，∠CAP=60°，且AP=AC，
∴△APC是等边三角形，
∴∠APC=60°，
∴∠BPM=60°，
又∵∠PBD=120°，
∴∠BPM+∠PBD=180°，
∴PM∥BD；
（2）如图1中，∵AM=MD，PM∥BD，
∴AP=PB，
∴PM= BD，
∵PA=PC=PB=BD，
∴PC=2PM；
（3）结论：tan∠BCM=．理由如下：
如图2，延长BM至点G，使得MG=MB，连接AG，BC，GC，PC，GD，
∵AM=MD，GM=BM，
∴四边形AGDB是平行四边形，
∴AG=BD，AG∥BD，
∴∠BAG=180°-∠ABD=60°，
∴∠CAG=120°，
∵△APC是等边三角形，
∴AC=CP，∠CPB=120°，
∵PB=DB=AG，
∴△CAG≌△CPB（SAS），
∴CG=CB，∠ACG=∠PCB，
∴∠GCB=60°，
∴△CBG是等边三角形，
∵GM=BM，
∴∠BCM=∠BCG=30°，
∴tan∠BCM=．
【点睛】本题属于几何变换综合题，考查了等边三角形的判定和性质，全等三角形的判定和性质，三角形中位线定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．
6．（2021·上海·九年级专题练习）如图，在中，，，，平分，交边于点，过点作的平行线，交边于点．
（1）求线段的长；
（2）取线段的中点，联结，交线段于点，延长线段交边于点，求的值．
【答案】（1）4；（2）
【分析】（1）分别求出CD，BC，BD，证明，根据相似性质即可求解；
（2）先证明，再证明，根据相似三角形性质求解即可．
【详解】解：（1）∵平分，，∴．
在中，，，，∴．
在中，，，，∴．
∴．
∵，
∴
∴．
∴．
（2）∵点是线段的中点，∴．
∵，
∴
∴．
∴．
∵，
∴
∴
∴．
【点睛】本题考查了含30°角的直角三角形性质，相似的判定与性质，解题的关键是能根据题意确定相似三角形，并根据相似性质解题．
题型三：“母子”型
1．（2021·上海黄浦·九年级期中）直线分别交x轴、y轴于A、B两点．
（1）求出点A、B的坐标；
（2）已知点G的坐标为（2，7），过点G和B作直线BG，连接AG，求∠AGB的正切值；
（3）在（2）的条件下，在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△AOB相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
【答案】（1），；（2）；（3）存在，，，，
【分析】（1）对于，令x＝0，则y＝1，令y＝0，即＝0，解得x＝3，即可求解；
（2）证明AG2＝AB2＋BG2，则△ABG为直角三角形，即可求解；
（3）分△ABQ∽△AOB、△ABQ∽△BOA两种情况，利用三角形相似边的比例关系，即可求解．
【详解】解：（1）对于，令x＝0，则y＝1，令y＝0，即＝0，解得x＝3，
故点A、B的坐标分别（3，0）、（0，1）；
（2）由A、B、G的坐标知，BG2＝22＋（7−1）2＝40，
同理AB2＝10，AG2＝50，
故AG2＝AB2＋BG2，
故△ABG为直角三角形，
则tan∠AGB＝；
（3）设直线BG的表达式为y＝kx＋b，则，
解得
故直线BG的表达式为y＝3x＋1，
设点Q（m，3m＋1），
①当△ABQ∽△AOB时，
则，即，
解得m＝±，
∴，
②当△ABQ∽△BOA时，
，即
解得：m＝±3，
∴，
故点P的坐标为（，2）或（−，0）或（3，10）或（−3，−8）．
【点睛】本题考查的是一次函数综合运用，涉及到一次函数的性质、解直角三角形、三角形相似等，其中（3），要注意分类求解，避免遗漏．
2．（2021·上海市金山初级中学九年级期中）如图，在△ABC中，点D在边AB上，点E、点F在边AC上，且DEBC，．
（1）求证：DFBE；
（2）如且AF＝2，EF＝4，AB＝6．求证△ADE∽△AEB．
【分析】（1）由题意易得，则有，进而问题可求证；
（2）由（1）及题意可知，然后可得，进而可证，最后问题可求证．
【详解】解：（1）∵DEBC，
∴，
∵，
∴，
∴DFBE；
（2）∵AF＝2，EF＝4，
∴由（1）可知，，AE=6，
∵AB＝6，
∴，
∴，
∴，
∵∠A=∠A，
∴△ADE∽△AEB．
【点睛】本题主要考查相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键．
3．（2021·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．
（1）求证：△BND∽△CNM；
（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．
【分析】（1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；
（2）先利用AD2=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=∠4，∠2=∠3，所以∠3=∠4，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．
【详解】证明：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
而BE=AB，
∴BE=CD，
而BE∥CD，
∴四边形BECD为平行四边形，
∴BD∥CE，
∵CM∥DB，
∴△BND∽△CNM；
（2）∵AD2=AB•AF，
∴AD：AB=AF：AD，
而∠DAB=∠FAD，
∴△ADB∽△AFD，
∴∠1=∠F，
∵CD∥AF，BD∥CE，
∴∠F=∠4，∠2=∠3，
∴∠3=∠4，
而∠NMC=∠CMD，
∴△MNC∽△MCD，
∴MC：MD=CN：CD，
∴MC•CD=MD•CN，
而CD=AB，
∴CM•AB=DM•CN．
【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．
4.（2022徐汇一模25题）如图，在中，，，点D为边AC上的一个动点，以点D为顶点作，射线DE交边AB于点E，过点B作射线DE的垂线，垂足为点F．
（1）当点D是边AC中点时，求的值；
（2）求证：；
（3）当时，求．

【小问1详解】解：过D作DH⊥AB于H，
在中，，，设，，
∴，
∵D为AC中点，∴AD= AC= ，∴，
∴，
在Rt△AHD中，，
∴BH=AB－AH= －= ，
在Rt△BHD中，；
【小问2详解】证明：∵∠BDE=∠A，∠DBE=∠ABD，∴△DEB∽△ADB，∴，
∵∠F=∠C=90°，∠BDE=∠A，∴△DFB∽△ACB，∴，∴即；
【小问3详解】解：由可设，，则DF=4k，
∵，∴ct∠BDE=ct∠A=，∴，
∴，又∠F=90°，
∴，
，
∵△DEB∽△ADB，∴即，
∴AB=8k，∴AE=AB－EB=5k，∴AE：EB=5k：3k=5：3．
5.（2022虹口一模25题）已知：如图，在△ABC中，∠ACB＝90°，AB＝10，tanB＝，点
D是边BC延长线上的点，在射线AB上取一点E，使得∠ADE＝∠ABC．过点A作AF⊥DE于点
F．
（1）当点E在线段AB上时，求证：＝；
（2）在（1）题的条件下，设CD＝x，DE＝y，求y关于x的函数关系式，并写出x的取值范围；
（3）记DE交射线AC于点G，当△AEF∽△AGF时，求CD的长．

【解答】（1）证明：∵∠ADE＝∠ABC，∠DAE＝∠BAD，
∴△ADE∽△ABD，∴，∵AF⊥DE，∴∠AFD＝∠ACB＝90°，
∴△ADF∽△ABC，∴，∴；
（2）解：∵∠ACB＝90°，tanB＝，∴tanB＝＝，
设AC＝3a，BC＝4a，∵AC2+BC2＝AB2，∴（3a）2+（4a）2＝102，
∴a＝2，∴AC＝6，BC＝8，∴AD＝＝，
由（1）得，∴，∴y＝，
当x＝0时，此时DE⊥AB，由S△ABC＝得，10•DE＝6×8，
∴DE＝，∴x＞；
（3）解：如图1，
当G在线段AC上时，延长AF交BC于M，作MN⊥AB于N，
∵△AEF∽△AGF，∴∠AEF＝∠AGF，∴AF＝AG，∴∠EAF＝∠GAF＝，
∵∠DAF＝∠BAC，∴∠DAC＝∠GAF，∵AC⊥BD，∴∠AMC＝∠ACD，
∴AM＝AD，∴CM＝CD，∵AM平分∠BAC，∴MN＝CM，
由S△ABC＝S△ABM+S△ACM得，，
∴16•CM＝48，∴CM＝3，∴CD＝3．
如图2，
当G点在AC的延长线上时，∵△AEF∽△AGF，∴∠AEF＝∠AGF，
∵∠AGF是∠AEF的外角，∴∠AGF＞∠AEF，∴这种情形不存在，∴CD＝3．
6.（2022长宁一模25题）已知, 在 中, , 点 是射线 上的动点, 点 是边 上的动点，且 , 射线 交射线 于点 ．
（1）如图 1, 如果 , 求 的值；
（2）联结, 如果 是以为腰的等腰三角形，求线段的长；
（3）当点在边上时, 联结, 求线段的长．
【详解】解：（1）∵AB＝AC，∴∠B＝∠C，∵OC＝OE，∴∠OEC＝∠C，
∴∠B＝∠OEC，∴△ABC∽△OEC，∴，∴，∴CE＝3.2，∴AE＝1.8；
∵∠AED＝∠OEC＝∠B，∠D＝∠D，∴△OBD∽△AED，
∴，∴．
（2）∵ 是以为腰的等腰三角形，∴AE＝OE，
∵OC＝OE，∴设AE＝OE＝OC=x，
由（1）得，△ABC∽△OEC，∴，∴，
解得，，经检验，是原方程的解；则的长是为．
（3）由（1）得，∠B＝∠OEC，∵∠OEC+∠OEA＝180°，∴∠B+∠OEA＝180°，
∴A、B、O、E四点共圆，∴∠DBE＝∠AOD，∵，∴，
∴AO∥DC，∴△AOE∽△CDE，△ABO∽△DBC，∴，，∴，
设OC=x，OB=8-x，∵△ABC∽△OEC，∴，∴，
解得，，∴∴，
解得，，（舍去），则的长是为．
7.【2021松江二模】如图，已知在△ABC中，BC＞AB，BD平分∠ABC，交边AC于点D，E是BC边上一点，且BE＝BA，过点A作AG∥DE，分别交BD、BC于点F、G，联结FE．
（1）求证：四边形AFED是菱形；
（2）求证：AB2＝BG•BC；
（3）若AB＝AC，BG＝CE，联结AE，求的值．
【分析】（1）由题目条件可证得△ABF≌△EBF（SAS）及△ABD≌△EBD（SAS），进而可推出AF＝FE＝ED＝DA，可得出四边形AFED是菱形．
（2）根据条件可证得△ABG∽△CBA，即可证明结论．
（3）由条件可得△DAE∽△ABC，由相似比可得，由BE2＝EC•BC，得到点E是BC的黄金分割点，可得出，即可得出结论．
【详解】（1）证明：∵BD平分∠ABC，∴∠ABF＝∠EBF，
∵BA＝BE，BF＝BF，∴△ABF≌△EBF（SAS），∴AF＝EF，
同理可得△ABD≌△EBD（SAS），∴AD＝ED，∠ADB＝∠EDB，
∵AG∥DE，∴∠AFD＝∠EDF，∴∠AFD＝∠ADF，∴AF＝AD，
∴AF＝FE＝ED＝DA，∴四边形AFED菱形．
（2）证明：由（1）得：△ABF≌△EBF，∴∠BAG＝∠BEF，
∵四边形AFED是菱形，∴AD∥FE，∴∠BEF＝∠C，∴∠BAG＝∠C，
∵∠ABG＝∠CBA，∴△ABG∽△CBA，∴，即AB2＝BG•BC．
（3）解：如图，
∵AB＝AC，∴∠ABG＝∠C，∵∠BAG＝∠C，∴∠ABG＝∠BAG，
∵∠AGC＝∠ABG＋∠BAG，∴∠AGC＝2∠BAG，∵BG＝CE，∴BE＝CG，
∴CG＝CA，∴∠CAG＝∠CGA，∵∠CAG＝2∠DAE，∴∠DAE＝∠ABC，
∴∠DEA＝∠ACB，∴△DAE∽△ABC，∴，
∵AB2＝BG•BC，AB＝BE，∴BE2＝EC•BC，∴点E是BC黄金分割点，
∴，∴，∵∠EAC＝∠C，∴CE＝AE，
∴，∴．
【点睛】本题考查了菱形的判定，相似三角形的性质与判定及黄金分割点等知识，综合性较强，熟练掌握相关知识并灵活运用所学知识求解是解题的关键．
题型四：“一线三等角”模型
1．（2021·上海市徐汇中学九年级阶段练习）已知：如图，四边形中，，，，平分．
（1）求证：四边形是菱形；
（2）如果点在对角线上，联结并延长，交边于点，交线段的延长线于点（点可与点重合），，设长度是是常数，且，，，求关于的函数关系式，并写出定义域；
（3）在第（2）小题的条件下，当是等腰三角形时，求的长（计算结果用含的代数式表示）
【答案】（1）见解析；（2）；（3）或时，为等腰三角形
【分析】（1）由题意先判断出∠DAC=∠DCA，∠BAC=∠BCA，进而得出∠DCA=∠BAC，∠DAC=∠BCA，即可得出结论；
（2）由题意先判断出△AEF∽△ABC，△ABC∽△BEC，得出比例式，即可得出结论；
（3）根据题意分三种情况，①当CE=EG时，判断出点F，G和点D重合，即：AF=AB，即可得出结论，②当CG=CE时，先判断出∠FDG=∠FGD，得出FG=FD，即可得出AF=BF，进而判断出FB=AC，即可得出结论；③当EG=GE时，判断出∠CEG=∠CBF，而∠CEG=∠CBF+∠ACB，进而判断出此种情况不存在．
【详解】解：（1）证明：，
，
又平分
，，
，
四边形为平行四边形
又
四边形是菱形；
（2）解：四边形是菱形，
，
，，
，
，
，
，
即
；
（3）解：是等腰三角形，
①当时，
，
，
，
，
，
此时，点，和点重合，
，
，
即，
②当时，
，
，
，
，
，
，
，
，
，
，
，
即
（负值已舍），
③当时，
，
，
，
，
此种情况不存在．
综上所述：或时，为等腰三角形．
【点睛】本题是四边形综合题，主要考查菱形的判定和性质，相似三角形的判定和性质，等腰三角形的判定和性质，分类讨论的思想，解答本题的关键是找出相关角之间关系．
2.（2018浦东新区二模）已知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE上CF＝CD，过点F作FG⊥FC交AD于点G．
（1）求证：GF＝GD；
（2）联结AF，求证：AF⊥DE．
整体分析：
根据等角的余角相等得到即可证明.
联结CG.证明△DAE≌△CDG,得到.进而得到，根据等边对等角得到根据三角形的内角和可以求出∠AFD= 90°，即可证明.
满分解答：
∵四边形是正方形，∴,
∵FG⊥FC， ∴∠GFC= 90°,
∵ ∴∠CDF=∠CFD ,
∴∠GFC-∠CFD=∠ADC-∠CDE，即∠GFD=∠GDF.
∴GF=GD.
联结CG.
∵ ∴点在线段的中垂线上,
∴GC⊥DE，
∴∠CDF+∠DCG= 90°，
∵∠CDF+∠ADE= 90°，
∴∠DCG=∠ADE
四边形是正方形,
∴AD=DC，∠DAE=∠CDG= 90°，
∴△DAE≌△CDG,
∴.
点是边的中点，
点是边的中点，
∴,
∴
∵
∴
∴∠AFD= 90°，即AF⊥DE.
点睛：属于四边形的综合题，考查了正方形的性质，全等三角形的判定与性质，等腰三角形的判定与性质等，考查知识点比较多，难度不大，熟练掌握各个知识点是解题的关键.
3．（2019·上海市育才初级中学九年级阶段练习）如图，在边长为6的正方形ABCD中，点E为AD边上的一个动点(与点A、D不重合)，∠EBM=45°，BE交对角线AC于点F，BM交对角线AC于点G、交CD于点M．
（1）如图1，联结BD，求证：，并写出的值；
（2）联结EG，如图2，若设，求y关于的函数解析式，并写出函数的定义域；
（3）当M为边DC的三等分点时，求的面积．
【答案】；；或
【分析】（1）根据正方形的性质得到∠EDB＝∠GCB＝45°，∠ABD＝∠CBD＝45°，根据相似三角形的判定定理证明即可；
（2）作EH⊥AC于H，根据等腰直角三角形的性质、勾股定理和相似三角形的性质得到y关于x的函数解析式；
（3）分CM＝CD和CM＝CD两种情况，根据相似三角形的性质解答即可．
【详解】（1）证明：∵四边形ABCD是正方形，
∴∠EDB＝∠GCB＝45°，∠ABD＝∠CBD＝45°，又∠EBM＝45°，
∴∠GBC＋∠DBM＝45°，∠EBD＋∠DBM＝45°，
∴∠GBC＝∠EBD，又∠EDB＝∠GCB＝45°，
∴△DEB∽△CGB，
∴DE：CG＝BD：BC＝；
（2）如图2，作EH⊥AC于H，
则AH＝EH＝x，
∵△DEB∽△CGB，
∴，
∴CG＝（6−x），
∴HG＝AC−AH−CG＝3，
∵EG2＝EH2＋HG2，
∴；
（3）当CM＝CD＝2时，
∵四边形ABCD是正方形，
∴CD∥AB，
∴，
∴CG＝，
∴DE＝3，则AE＝3，
∴AH＝EH＝，
∵AD∥BC，
∴，
∴AF＝2，
∴GF＝AC−AF−CG＝，
∴S△EGF＝×FG×EH＝，
当CM＝CD＝4时，
，
∴CG＝，
∴DE＝，则AE＝，
AH＝EH＝，
∵，
∴AF＝，
∴GF＝AC−AF−CG＝，
∴S△EGF＝×FG×EH＝．
综上,S△EGF=或
【点睛】本题考查相似三角形的判定和性质的应用、正方形的性质的应用，正确作出辅助线、灵活运用相关的定理是解题的关键，注意分情况讨论思想的运用．
4．（2020·上海宝山·九年级阶段练习）如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．
（1）求证：AB·AF＝CB·CD；
（2）已知AB＝15 cm，BC＝9 cm，P是射线DE上的动点．设DP＝x cm（），四边形BCDP的面积为y cm2．
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值．
【答案】（1）见解析；（2）①（）；②当时，△PBC的周长最小，此时．
【分析】（1）由已知条件易证△DCF∽△ABC，可得，即可得AB·AF＝CB·CD；
（2）①由勾股定理求得AC=12，即可得CF＝AF＝6，根据四边形BCDP的面积=△DCP的面积+△BCP的面积即可得y关于x的函数关系式；
②由题意可知△PBC的周长最小，就是PB＋PC最小，当当P、A、B三点共线时PB＋PA最小．这时求得x、y的值即可．
【详解】（1）证明：∵AD＝CD，DE⊥AC，
∴DE垂直平分AC
∴AF＝CF，∠DFA＝∠DFC＝90°，∠DAF＝∠DCF．
∵∠DAB＝∠DAF＋∠CAB＝90°，∠CAB＋∠B＝90°，
∴∠DCF＝∠DAF＝∠B
在Rt△DCF和Rt△ABC中，
∠DFC＝∠ACB＝90°，∠DCF＝∠B
∴△DCF∽△ABC
∴，即．
∴AB·AF＝CB·CD
（2）解①∵AB＝15 BC＝9 ∠ACB＝90°
∴AC＝＝＝12
∴CF＝AF＝6
∴y=（x+9）×6＝3x＋27（x＞0）
②∵BC＝9（定值），
∴△PBC的周长最小，就是PB＋PC最小．
由（1）可知，点C关于直线DE的对称点是点A，
∴PB＋PC＝PB＋PA，故只要求PB＋PA最小．
显然当P、A、B三点共线时PB＋PA最小．
此时DP＝DE，PB＋PA＝AB．
由（1），∠ADF＝∠FAE，∠DFA＝∠ACB＝90°，得△DAF∽△ABC．
由EF∥BC，得AE＝BE＝AB＝，EF＝．
∴AF∶BC＝AD∶AB，
即6∶9＝AD∶15．
∴AD＝10．
Rt△ADF中，AD＝10，AF＝6，∴DF＝8．
∴DE＝DF＋FE＝8＋＝．
∴当x＝时，△PBC的周长最小，此时y＝
5．（2021·上海·九年级专题练习）（1）正方形中，对角线与相交于点，如图1，请直接猜想并写出与之间的数量关系：________；
（2）如图2，将（1）中的绕点逆时针旋转得到，连接，，请猜想线段与的数量关系，并证明你的猜想；
（3）如图3，矩形和有公共顶点，且，，则________．
【答案】（1）AO＝CD；（2），见解析；（3）
【分析】(1)根据正方形的性质可得，,由锐角三角比可得AO与CD的关系；
(2)由正方形性质可得，△ABC和△OBC都是等腰直角三角形，得,由旋转可得BC1＝BO1，易证△BDC1∽△BAO1,可得，即;
(3)由∠EBF＝∠ABD＝30°，运用锐角三角比可得，易证∠EBA＝∠FBD，可得△AEB∽△FBD，即.
【详解】
解：(1) ∵四边形ABCD为正方形，
∴,
∴AO＝CD．
(2) 如图2，
∵四边形ABCD为正方形，
∴AB＝BC，AC＝BD，OB＝OC，∠OBC＝∠ABO＝45°，∠BOC＝90°，
∴△ABC和△OBC都是等腰直角三角形，
∴，，
∴，
∵△BOC绕点B逆时针方向旋转得到△BO1C1，
∴∠O1BC1＝∠OBC＝45°，OB＝O1B，BC1＝BC，
∴BC1＝BO1，
∵∠1+∠3＝45°，∠2+∠3＝45°，
∴∠1＝∠2，
∴△BDC1∽△BAO1
∴，
∴
(3) 如图3 在Rt△EBF中，cs∠EBF＝
在Rt△ABD中，cs∠ABD＝，
∵∠EBF＝∠ABD＝30°，
∴，
∵∠EBF+∠FBA＝∠ABD+∠FBA，
即∠EBA＝∠FBD，
∴△AEB∽△FBD，
∴.
【点睛】本题考查了正方形的性质，锐角三角比以及相似三角形的判定与性质，较为综合，熟练分析图形，寻找相等的角与相似三角形是解题的关键.
题型五：旋转型相似
1．（2021秋•静安区期末）如图1，四边形ABCD中，∠BAD的平分线AE交边BC于点E，已知AB＝9，AE＝6，AE2＝AB•AD，且DC∥AE．
（1）求证：DE2＝AE•DC；
（2）如果BE＝9，求四边形ABCD的面积；
（3）如图2，延长AD、BC交于点F，设BE＝x，EF＝y，求y关于x的函数解析式，并写出定义域．
【分析】（1）先证明△ABE∽△AED，可得∠AEB＝∠ADE，再由平行线性质可推出∠ADE＝∠DCE，进而证得△ADE∽△ECD，根据相似三角形性质可证得结论；
（2）如图2，过点B作BG⊥AE，运用等腰三角形性质可得G为AE的中点，进而可证得△ADE≌△ECD（SAS），再求得S△ABE＝×AE×BG＝18，根据△ABE∽△AED且相似比为3：2，可求得S△AED＝S△CDE＝8，由S四边形ABCD＝S△ABE+S△AED+S△CDE可求得答案；
（3）由△ABE∽△AED，可求得：DE＝x，进而得出DC＝x2，再利用△ADE∽△ECD，可得：CE＝x，再利用DC∥AE，可得△AEF∽△DCF，进而求得：CF＝EF，再结合题意得出答案．
【解答】（1）证明：如图1，∵AE平分∠BAD，
∴∠BAE＝∠DAE，
∵AE2＝AB•AD，
∴＝，
∴△ABE∽△AED，
∴∠AEB＝∠ADE，
∵DC∥AE，
∴∠AEB＝∠DCE，∠AED＝∠CDE，
∴∠ADE＝∠DCE，
∴△ADE∽△ECD，
∴＝，
∴DE2＝AE•DC；
（2）解：如图2，过点B作BG⊥AE，
∵BE＝9＝AB，
∴△ABE是等腰三角形，
∴G为AE的中点，
由（1）可得△ADE、△ECD也是等腰三角形，
∵AE2＝AB•AD，AB＝BE＝9，AE＝6，
∴AD＝4，DE＝6，CE＝4，AG＝3，
∴△ADE≌△ECD（SAS），
在Rt△ABG中，BG＝＝＝6，
∴S△ABE＝×AE×BG＝×6×6＝18，
∵△ABE∽△AED且相似比为3：2，
∴S△ABE：S△AED＝9：4，
∴S△AED＝S△CDE＝8，
∴S四边形ABCD＝S△ABE+S△AED+S△CDE＝18+8+8＝34；
（3）解：如图3，由（1）知：△ABE∽△AED，
∴＝，
∵BE＝x，AB＝9，AE＝6，AE2＝AB•AD，AD＝4，
∴＝，
∴DE＝x，
由（1）知：DE2＝AE•DC，
∴DC＝x2，
∵△ADE∽△ECD，
∴＝＝，
∴CE＝x，
∵DC∥AE，
∴△AEF∽△DCF，
∴＝＝，
∴CF＝EF，
∴＝＝＝，
∴y＝EF＝CE＝×x＝，
∵即，
∴3＜x＜9，
∴y关于x的函数解析式为y＝，定义域为3＜x＜9．
【点评】本题是相似三角形综合题，考查了角平分线定义，平行线的性质，勾股定理，相似三角形的判定和性质，等腰三角形的性质，三角形面积等知识，熟练掌握相似三角形的判定和性质是解题关键．
2．（2018·上海民办浦东交中初级中学八年级阶段练习）如图，在平面直角坐标系中，矩形的两边分别在轴、轴的正半轴上，.点从点出发，沿轴以每秒个单位长的速度向点匀速运动，当点到达点时停止运动，设点运动的时间是t秒.将线段的中点绕点按顺时针方向旋转，得点，点随点的运动而运动，连接.
(1)请用含t的代数式表示出点的坐标.
(2)求为何值时，的面积最大，最大为多少?
(3)在点从向运动的过程中，能否成为直角三角形?若能，求的值:若不能，请说明理由.
(4)请直接写出整个运动过程中，点所经过的长度.
【答案】；；能，2或；
【分析】（1）设出P点的坐标，再求出CP的中点坐标，根据相似的性质即可求出点D的坐标；
（2）根据点D的坐标及三角形的面积公式直接求解即可；
（3）先判断出可能为直角的角，再根据勾股定理求解；
（4）根据点D的运动路线与OB平行且相等即可解决
【详解】（1）∵点P从点出发，沿轴以每秒个单位长的速度向点匀速运动


设CP的中点为F，过点D作DE⊥OA，垂足为E，
∵

∵F绕点P顺时针旋转90°得到点D


又





（2）∵

∴当时，最大，为4
（3）能构成直角三角形
当时，
由勾股定理得，
即
解得 或（舍去）
当时，此时点D在AB上




即
∴
综上所述，或时，能成为直角三角形
（4）当点P在原点O处时，对应的
当点D运动时，直线 的斜率 ，即无论点D如何运动，直线的斜率为固定值，即点D的运动轨迹始终在直线上，

∴点D的运动路线与OB平行
当点P运动到A时， ，此时 的坐标为
即点D的运动轨迹为线段
∵点与点B,C共线
∴轴
∵四边形为平行四边形
∴点D的运动路线与OB平行且相等
∵
∴点D运动路线的长为
【点睛】本题主要考查四边形综合问题，掌握矩形的性质，相似三角形的判定及性质，分情况讨论是解题的关键．