沪教版数学九年级上册期末复习训练重难点03二次函数综合（7种题型）（2份，原卷版+解析版）

这是一份沪教版数学九年级上册期末复习训练重难点03二次函数综合（7种题型）（2份，原卷版+解析版），文件包含沪教版数学九年级上册期末复习训练重难点03二次函数综合7种题型原卷版doc、沪教版数学九年级上册期末复习训练重难点03二次函数综合7种题型解析版doc等2份试卷配套教学资源，其中试卷共180页， 欢迎下载使用。
题型一：特殊三角形问题
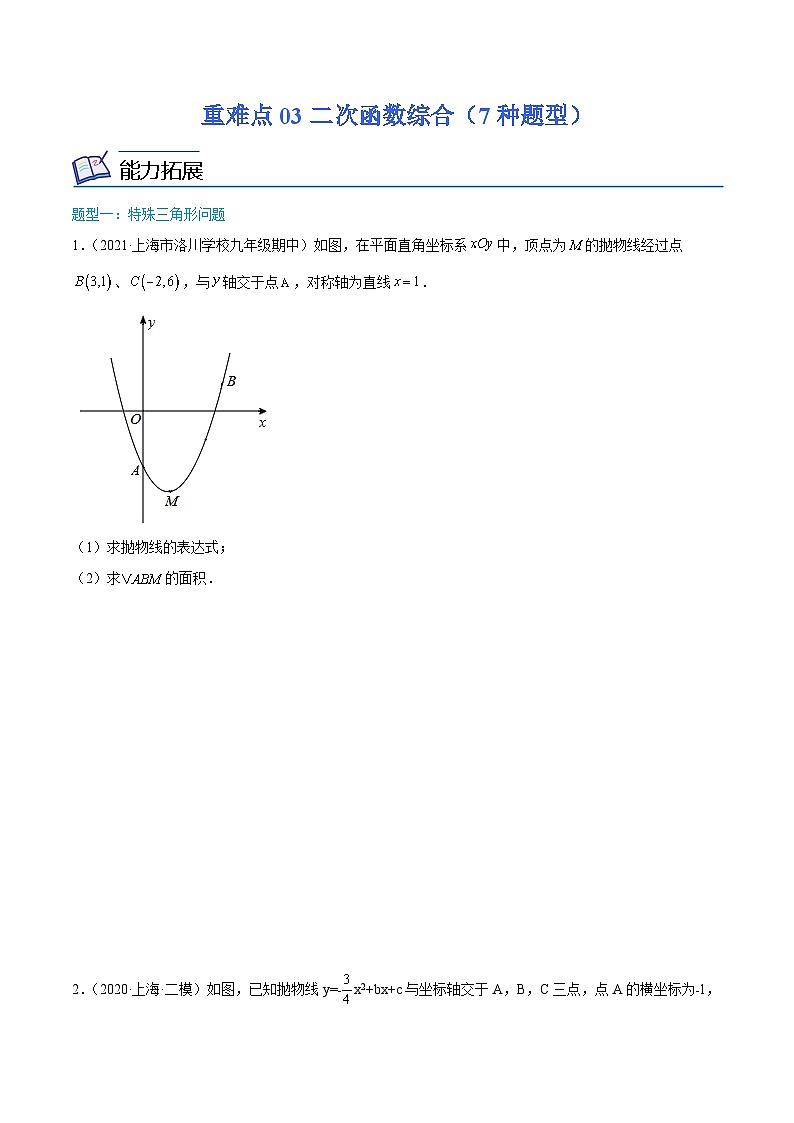
1．（2021·上海市洛川学校九年级期中）如图，在平面直角坐标系中，顶点为的抛物线经过点、，与轴交于点，对称轴为直线．
（1）求抛物线的表达式；
（2）求的面积．
2．（2020·上海·二模）如图，已知抛物线y=﹣x2+bx+c与坐标轴交于A，B，C三点，点A的横坐标为﹣1，过点C（0，3）的直线y=﹣x+3与x轴交于点Q，点P是线段BC上的一个动点，PH⊥OB于点H．若PB=5t，且0＜t＜1．
（1）确定b，c的值；
（2）写出点B，Q，P的坐标（其中Q，P用含t的式子表示）；
（3）依点P的变化，是否存在t的值，使△PQB为等腰三角形？若存在，求出所有t的值；若不存在，说明理由．
3．（2022·上海市奉贤区汇贤中学九年级期中）如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与直线y＝x﹣3分别交x轴、y轴上的B、C两点，设该抛物线与x轴的另一个交点为点A，顶点为点D，连接CD交x轴于点E．
（1）求该抛物线的表达式及点D的坐标；
（2）求∠DCB的正切值；
（3）如果点F在y轴上，且∠FBC＝∠DBA+∠DCB，求点F的坐标．
4．（2022·上海虹口·二模）如图，在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点，顶点为，连接交抛物线的对称轴于点．
(1)求抛物线的表达式；
(2)连接、，点是射线上的一点，如果，求点的坐标；
(3)点是线段上的一点，点是对称轴右侧抛物线上的一点，如果是以为腰的等腰直角三角形，求点的坐标．
5．（2022·上海普陀·二模）如图，在平面直角坐标系中，已知抛物线与x轴交于点、，与y轴交于点C，顶点为D．
(1)求抛物线的表达式和点D的坐标；
(2)点E是第一象限内抛物线的一个动点，其横坐标为m，直线交y轴于点F．
①用m的代数式表示直线的截距；
②在的面积与的面积相等的条件下探究：在y轴右侧存在这样一条直线，满足：以该直线上的任意一点及点C、F三点为顶点的三角形的面积都等于面积，试用规范、准确的数学语言表达符合条件的直线．
题型二：面积问题
1．（2021·上海宝山·三模）如图，在直角坐标平面xOy内，点A在x轴的正半轴上，点B在第一象限内，且∠OAB＝90°，∠BOA＝30°，OB＝4.，二次函数y＝﹣x2＋bx的图象经过点A，顶点为点C．
（1）求这个二次函数的解析式，并写出顶点C的坐标；
（2）设这个二次函数图象的对称轴l与OB相交于点D，与x轴相交于点E，求的值；
（3）设P是这个二次函数图象的对称轴l上一点，如果△POA的面积与△OCE的面积相等，求点P的坐标．
2．（2020·上海市徐汇中学九年级期中）在平面直角坐标系xOy中，抛物线y＝﹣x2+mx+n经过点A（4，﹣1），B（1，2）
（1）求抛物线的表达式及对称轴；
（2）该抛物线对称轴与抛物线交于点C，连接BA、BC，求△ABC的面积．
3．（2021·上海市奉贤区实验中学九年级期中）如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣2ax﹣3与x轴和y轴分别交于A、B两点，抛物线的顶点为C（c，-4），联结AB、AC、BC．
（1）求这条抛物线的表达式和c的值；
（2）求△ABC的面积；
（3）在y轴上找一个点M（点M不与点B重合），使得∠AMC＝90°，并将△AMC沿直线AC翻折，得到△ANC，求点N的坐标．
4．（2022·上海金山区世界外国语学校一模）在平面直角坐标系中（如图），已知点，点与点关于轴对称．抛物线经过原点，且顶点为，将该抛物线与x轴的另外一个交点记为．
(1)求抛物线的表达式；
(2)如果点在抛物线上，且，求点的坐标；
(3)在抛物线的对称轴上是否存在一点，使得抛物线上的任意一点到点的距离都等于点到直线的距离？如果存在，试求点的坐标；如果不存在，请简述理由．
5．（2022·上海松江·九年级期末）如图，已知直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过A、B两点．
(1)求这条抛物线的表达式；
(2)直线x＝t与该抛物线交于点C，与线段AB交于点D（点D与点A、B不重合），与x轴交于点E，联结AC、BC．
①当＝时，求t的值；
②当CD平分∠ACB时，求ABC的面积．
6．（2022·上海·一模）如图，在平面直角坐标系xOy中，顶点为M的抛物线经过点B（3，1）、C（﹣2，6），与y轴交于点A，对称轴为直线x＝1．
(1)求抛物线的表达式；
(2)求△ABM的面积；
(3)点P是抛物线上一点，且∠PMB＝∠ABM，试直接写出点P的坐标．
7．（2022·上海·位育中学模拟预测）如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣4ax+3与x轴交于A、B两点（点A在点B的左侧），且AB＝2，抛物线与y轴交于点C．
(1)求抛物线的解析式；
(2)求∠ACB的正切值；
(3)若点D在抛物线上，且S△BCD＝3，请直接写出所有满足条件的点D坐标．
8．（2022·上海·格致中学二模）如图，在平面直角坐标系中，已知抛物线与轴交于点、两点（点在点的左侧），与轴交于点，对称轴与轴交于点，直线经过点，交抛物线的对称轴于点.
(1)求的面积；
(2)联结，交轴于点，联结，若，求抛物线的表达式；
(3)在（2）的条件下，点是直线上一点，且，求点的坐标.
9．（2021·上海市新泾中学九年级期中）如图，抛物线（）经过点，与轴的负半轴交于点，与轴交于点，且，抛物线的顶点为．
（1）求这条抛物线的表达式；
（2）联结、、、AB，求四边形的面积；
（3）如果点E在轴的正半轴上，且，求点E的坐标．
10．（2022·上海市娄山中学九年级期中）如图，已知在平面直角坐标系xOy中，抛物线y=-x2+bx+c经过点A（-2，0）．与点C（0，4）．与x轴的正半轴交于点B．
(1)求抛物线的表达式；
(2)如果D是抛物线上一点，AD与线段BC相交于点E，且AD将四边形ABDC分成面积相等的两部分，求的值；
(3)如果P是x轴上一点，∠PCB=∠ACO，求∠PCO的正切值．
题型三：线段周长问题
1．（2022·上海·九年级单元测试）如图，二次函数的图像与x轴交于A、B两点，与y轴相交于点C，点A的坐标为，是抛物线上一点（点与点、、都不重合）．
(1)求抛物线解析式；
(2)求点B的坐标；
(3)设直线PB与直线AC相交于点M，且存在这样的点P，使得，试确定点的横坐标．
2．（2022·上海金山区世界外国语学校一模）在平面直角坐标系中（如图），已知点，点与点关于轴对称．抛物线经过原点，且顶点为，将该抛物线与x轴的另外一个交点记为．
(1)求抛物线的表达式；
(2)如果点在抛物线上，且，求点的坐标；
(3)在抛物线的对称轴上是否存在一点，使得抛物线上的任意一点到点的距离都等于点到直线的距离？如果存在，试求点的坐标；如果不存在，请简述理由．
3．（2021·上海市民办上宝中学九年级期中）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过A（0，﹣1），B（4，1）．直线AB交x轴于点C，P是直线AB下方抛物线上的一个动点．过点P作PD⊥AB，垂足为D，PEx轴，交直线AB于点E．
(1)求抛物线的函数表达式；
(2)如图1，在抛物线上有一点F，使得∠CBF＝∠OAC，求点F的坐标；
(3)如图2，当△PDE的周长为+8时，求点P的坐标．
4．（2022·上海闵行·二模）如图，在平面直角坐标系中，抛物线与x轴相交于点，，与y轴交于点C.将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段于点E，交抛物线于点F，过点F作直线的垂线，垂足为点G.
(1)求抛物线的表达式；
(2)以点G为圆心，为半径画；以点E为圆心，为半径画.当与内切时.①试证明与的数量关系；②求点F的坐标.
题型四：角度问题
1．（2021·上海市民办新北郊初级中学九年级期末）如图，已知二次函数y＝﹣x2＋2mx＋3m2（m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．
(1)点B的坐标为 ，点D的坐标为 ；（用含有m的代数式表示）
(2)连接CD，BC．
①若CB平分∠OCD，求二次函数的表达式；
②连接AC，若CB平分∠ACD，求二次函数的表达式．
2．（2022·上海虹口·九年级期中）如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．
（1）求抛物线的解析式；
（2）过点A的直线交直线BC于点M．
①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；
②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．
3．（2021·上海·九年级期末）如图，在平面直角坐标系中，已知点、、，抛物线经过、两点．
（1）当该抛物线经过点时，求该抛物线的表达式；
（2）在（1）题的条件下，点为该抛物线上一点，且位于第三象限，当时，求点的坐标；
（3）如果抛物线的顶点位于内，求的取值范围．
4．（2021·上海市实验学校二模）已知直线交x轴于点A，交y轴于点C（0,4），抛物线经过点A，交y轴于点B（0，-2），点P为抛物线上一个动点，设P的横坐标为m（m＞0），过点P作x轴的垂线PD，过点B作BD⊥PD于点D，联结PB．
（1）求抛物线的解析式；
（2）当△BDP为等腰直角三角形时，求线段PD的长；
（3）将△BDP绕点B旋转得到△且旋转角∠PB=∠OAC，当点P对应点落在y轴上时，求点P的坐标．
5．（2022·上海·二模）将抛物线，与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C，顶点为D．
（1）求抛物线的表达式和点D的坐标；
（2）∠ACB与∠ABD是否相等？请证明你的结论；
（3）点P在抛物线的对称轴上，且△CDP与△ABC相似，求点P的坐标．
题型五：特殊四边形问题
一、解答题
1．（2021·上海宝山·九年级期末）已知抛物线y＝ax2+bx（a≠0）经过A(4，0)，B(﹣1，3)两点，抛物线的对称轴与x轴交于点C，点D与点B关于抛物线的对称轴对称，连接BC、BD．
(1)求该抛物线的表达式以及对称轴；
(2)点E在线段BC上，当∠CED＝∠OBD时，求点E的坐标；
(3)点M在对称轴上，点N在抛物线上，当以点O、A、M、N为顶点的四边形是平行四边形时，求这个平行四边形的面积．
2．（2022·上海崇明·九年级期末）如图，抛物线y=−x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．
(1)求抛物线的解析式，并写出此抛物线的对称轴和顶点坐标；
(2)如果以点P、N、B、O为顶点的四边形为平行四边形，求m的值；
(3)如果以B、P、N为顶点的三角形与△ABO相似，求点M的坐标．
3．（2021·上海徐汇·二模）如图，已知抛物线y＝x2+m与y轴交于点C，直线y＝﹣x+4与y轴和x轴分别交于点A和点B，过点C作CD⊥AB，垂足为点D，设点E在x轴上，以CD为对角线作▱CEDF．
（1）当点C在∠ABO的平分线上时，求上述抛物线的表达式；
（2）在（1）的条件下，如果▱CEDF的顶点F正好落在y轴上，求点F的坐标；
（3）如果点E是BO的中点，且▱CEDF是菱形，求m的值．
4．（2022·上海徐汇·二模）如图，在平面直角坐标系中，二次函数的图像与x轴交于A和点B（点A在点B的左侧），与y轴交于点C，且AB＝4．
(1)求这个函数的解析式，并直接写出顶点D的坐标；
(2)点E是二次函数图像上一个动点，作直线轴交抛物线于点F（点E在点F的左侧），点D关于直线EF的对称点为G，如果四边形DEGF是正方形，求点E的坐标；
(3)若射线AC与射线BD相交于点H，求∠AHB的大小．
5．（2022·上海市奉贤区华亭学校九年级期中）如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴相交点A（-1，0）和点B（3，0），与y轴相交于点C，抛物线的顶点为点D，对称轴交x轴于点E，点Q为线段DE上一点，联结AC．
(1)求这条抛物线的表达式及对称轴；
(2)当∠ACO=∠QOE时，求的值；
(3)当∠ACO=∠QOC时，判断四边形ACQO的形状；
(4)（附加题）当∠ACO=∠AQE时，求∠BQE的余切值；
(5)（附加题）当∠ACO=∠CBQ时，判断△BCQ的形状．
题型六：相似三角形问题
一、解答题
1．（2022·上海静安·九年级期末）如图，在平面直角坐标系中，已知抛物线经过点A（2，0）和点，顶点为点D．
(1)求直线AB的表达式；
(2)求tan∠ABD的值；
(3)设线段BD与轴交于点P，如果点C在轴上，且与相似，求点C的坐标．
2．（2022·上海徐汇·九年级期末）如图，抛物线与x轴相交于点A，与y轴交于点B，C为线段OA上的一个动点，过点C作x轴的垂线，交直线AB于点D，交该抛物线于点E．
(1)求直线AB的表达式，直接写出顶点M的坐标；
(2)当以B，E，D为顶点的三角形与相似时，求点C的坐标；
(3)当时，求与的面积之比．
3．（2022·上海嘉定·九年级期末）在平面直角坐标系中，点、两点在直线上，如图．二次函数的图像也经过点、两点，并与轴相交于点，如果轴，点的横坐标是．
(1)求这个二次函数的解析式；
(2)设这个二次函数图像的对称轴与交于点，点在轴的负半轴上，如果以点、、所组成的三角形与相似，且相似比不为，求点的坐标；
(3)设这个二次函数图像的顶点是，求的值．
4．（2021·上海市文来中学九年级期中）如图，在平面直角坐标系xOy中，抛物线经过点，，且与y轴交于点A．
(1)求抛物线的表达式及点A的坐标；
(2)点P是y轴右侧抛物线上的一点，过点P作，交线段OA的延长线于点Q，如果，求证：；
(3)若点F是线段AB（不包含端点）上的一点，且点F关于AC的对称点恰好在上述抛物线上，求直线的解析式．
5．（2022·上海理工大学附属初级中学一模）已知矩形OABC在平面直角坐标系中的位置如图所示，A、C两点的坐标分别为，，直线与边BC相交于点D．
(1)求点D的坐标；
(2)若抛物线经过A、D两点，试确定此抛物线的解析式；
(3)在（2）中的抛物线的对称轴与直线AD交于点M，点P在对称轴上，且△PAM与△ABD相似，求点P的坐标．
6．（2022·上海青浦·九年级期末）如图，在平面直角坐标系xOy中，抛物线与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C，顶点为点D．
(1)求该抛物线的表达式及点C的坐标；
(2)联结BC、BD，求∠CBD的正切值；
(3)若点P为x轴上一点，当△BDP与△ABC相似时，求点P的坐标．
7．（2022·上海市罗山中学九年级期中）如图，在平面直角坐标系xOy中，顶点为M的抛物线经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=1200．
（1）求这条抛物线的表达式；
（2）连接OM，求∠AOM的大小；
（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．
8．（2022·上海崇明·二模）如图．在平面直角坐标系中，抛物线与x轴交于点A、B，与y轴交于点C，点A的坐标为，对称轴为直线．点M为线段OB上的一个动点，过点M作直线l平行于y轴交直线BC于点F，交抛物线于点E．
(1)求抛物的解析式；
(2)当以C、E、F为顶点的三角形与相似时，求线段EF的长度：
(3)如果将沿直线CE翻折，点F恰好落在y轴上点N处，求点N的坐标．
9．（2022·上海·虹口实验学校九年级期中）如图，在平面直角坐标系中，直线分别交轴、轴于、两点，抛物线经过点和点，且其顶点为，点为抛物线与轴的另一个交点
(1)求抛物线的表达式；
(2)求的正切值；
(3)点在抛物线上，若，求点的坐标．
(4)连接，延长交轴于点，点是直线上的动点，如果与是相似三角形，求点的坐标．
题型七：其他问题
一、填空题
1．（2022·上海·九年级单元测试）若抛物线的顶点为，抛物线的顶点为B，且满足顶点A在抛物线上，顶点B在抛物线上，则称抛物线与抛物线互为“关联抛物线”，已知顶点为M的抛物线与顶点为N的抛物线互为“关联抛物线”，直线MN与轴正半轴交于点D，如果，那么顶点为N的抛物线的表达式为_________
二、解答题
2．（2022·上海松江·二模）如图，在平面直角坐标系中，已知直线与轴交于点A、与轴交于点，抛物线经过点A、．
(1)求抛物线的表达式；
(2)是抛物线上一点，且位于直线上方，过点作轴、轴，分别交直线于点、．
①当时，求点的坐标；
②连接交于点，当点是的中点时，求的值．
3．（2022·上海奉贤·二模）如图，在平面直角坐标系中，直线与x轴、y轴分别交于点A、B．抛物线经过点A、B顶点为C．
(1)求该抛物线的表达式；
(2)将抛物线沿y轴向上平移，平移后所得新抛物线顶点为D，如果，求平移的距离；
(3)设抛物线上点M的横坐标为m，将抛物线向左平移3个单位，如果点M的对应点Q落在内，求m的取值范围．
4．（2022·上海民办永昌学校九年级期中）已知：抛物线经过，,．
(1)求：抛物线的解析式；
(2)设抛物线的顶点为P，把翻折，使点P落在线段AB上（不与A、B重合），记作，折痕为EF，设，，求y关于x的函数关系式，并写出定义域；
(3)当点在线段AB上运动但不与A、B重合时，能否使的一边与x轴垂直？若能，请求出此时点的坐标；若不能，请你说明理由．
5．（2022·上海市建平实验中学九年级期末）如图，在平面直角坐标系中，抛物线y＝ax2﹣x﹣4与x轴交于点A（4，0），与y轴交于点C．点B（12，0），联结BC．
(1)求该抛物线解析式；
(2)求∠ACB的正弦值；
(3)如图，点D为抛物线上一点，直线AD交y轴于点E，交线段BC于点F．若△ECA∽△EFC，求点D的坐标．
6．（2022·上海虹口·九年级期末）已知开口向上的抛物线与y轴的交点为A，顶点为B，点A与点C关于对称轴对称，直线AB与OC交于点D．
(1)求点C的坐标，并用含a的代数式表示点B的坐标；
(2)当时，求抛物线的表达式；
(3)当时，求OD的长．
7．（2020·上海市徐汇中学九年级期中）如图，在平面直角坐标系中，矩形OABC的顶点A（3，0），C（0，1）．将矩形OABC绕原点逆时针旋转90°，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线y＝ax2+bx+c的图象经过点C′、M、N．解答下列问题：
（1）求出该抛物线所表示的函数解析式；
（2）在抛物线上有一点E，且点E在C′的左侧，过点E作EF⊥x轴，垂足为点F，若△EFM与△MON相似，求点E的坐标；
（3）在抛物线上是否存在一点P（C′点除外），使得∠PMN＝∠OMN，若存在，写出点P坐标，不存在，写出理由．
8．（2022·上海徐汇·九年级阶段练习）如图所示，抛物线的图像与x轴交于A、B两点，与y轴交于点C．
（1）当时 ，
①求点A、B、C的坐标；
②如果点P是抛物线上一点，点M是该抛物线对称轴上的点，当是以为斜边的等腰直角三角形时，求出点P的坐标；
（2）点D是抛物线的顶点，连接、，当四边形是圆的内接四边形时，求a的值．