新高考数学一轮复习考点精讲+题型精练专题18 函数 y=Asin(wx+φ)的图象和性质与三角函数模型的应用（2份，原卷版+解析版）

这是一份新高考数学一轮复习考点精讲+题型精练专题18 函数 y=Asin(wx+φ)的图象和性质与三角函数模型的应用（2份，原卷版+解析版），文件包含新高考数学一轮复习考点精讲+题型精练专题18函数yAsinwx+φ的图象和性质与三角函数模型的应用原卷版doc、新高考数学一轮复习考点精讲+题型精练专题18函数yAsinwx+φ的图象和性质与三角函数模型的应用解析版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
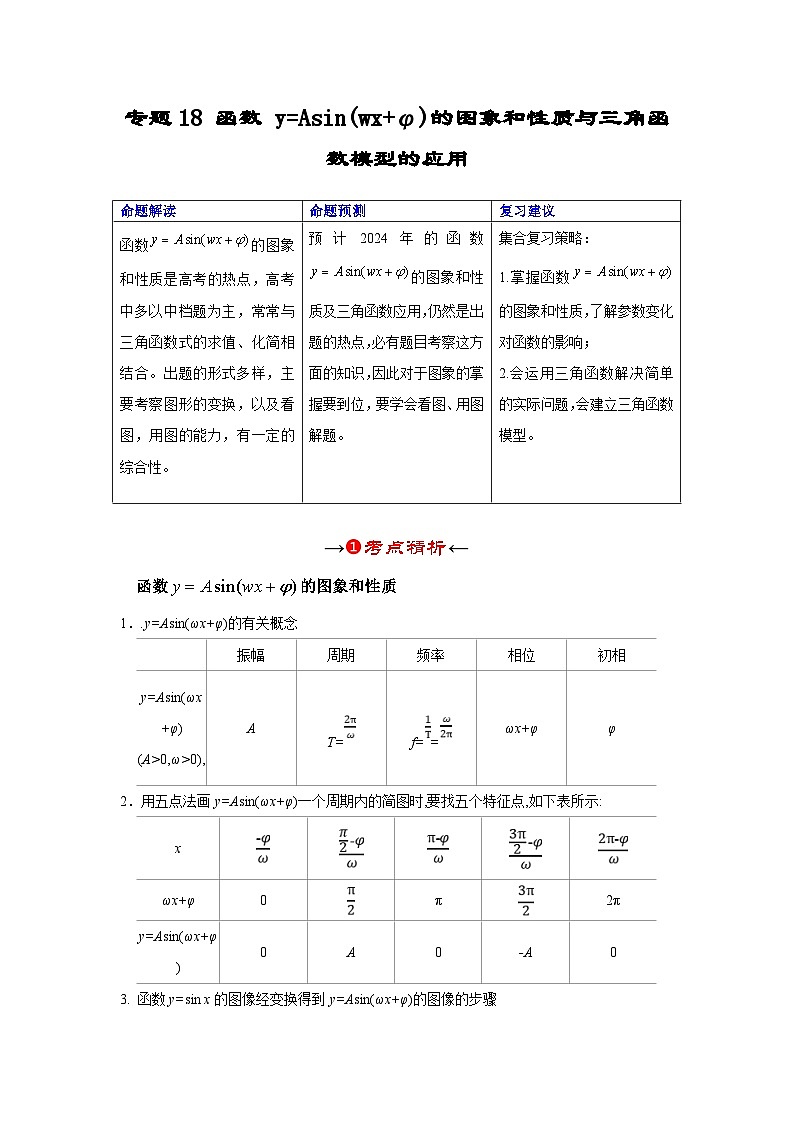
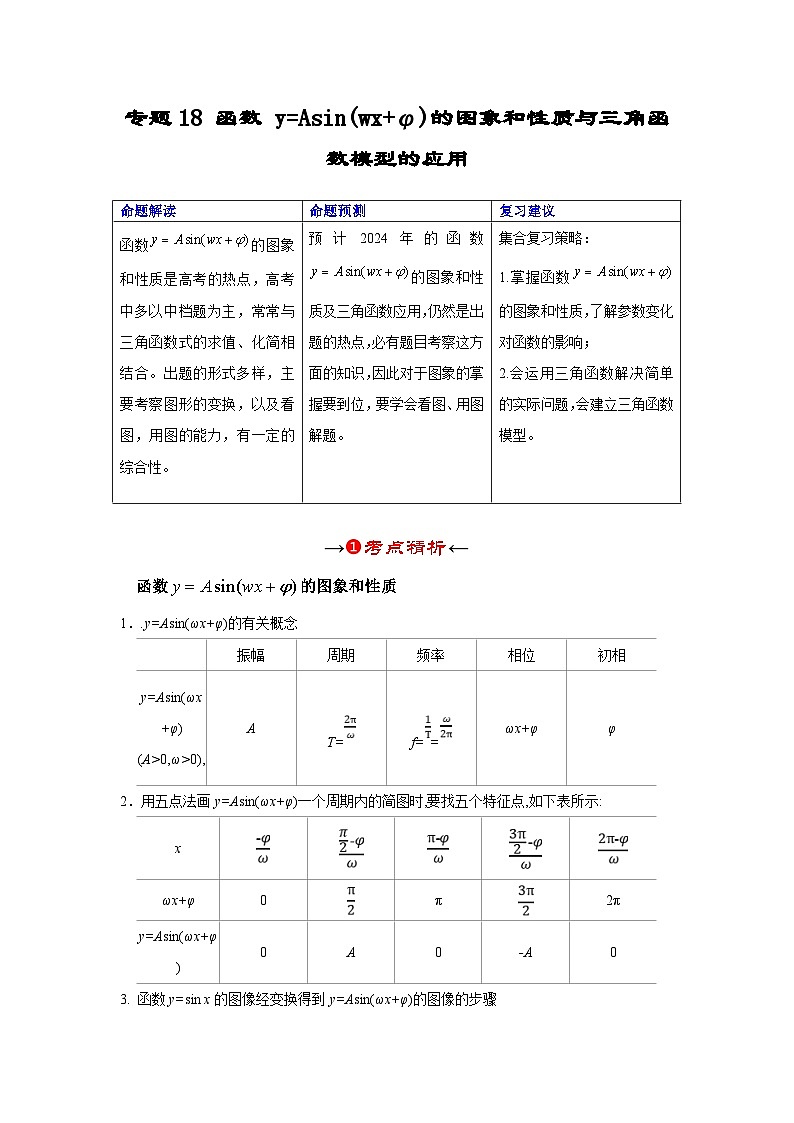
专题18 函数 y=Asin(wx+φ)的图象和性质与三角函数模型的应用
№考向解读
➊考点精析
➋真题精讲
➌模拟精练
➍专题训练
（新高考）
高考数学一轮复习
专题18 函数 y=Asin(wx+φ)的图象和性质与三角函数模型的应用
→➊考点精析←
函数的图象和性质
1．.y=Asin(ωx+φ)的有关概念
2．用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个特征点,如下表所示:
3. 函数y=sin x的图像经变换得到y=Asin(ωx+φ)的图像的步骤
→➋真题精讲←
1. （2023全国甲卷10）函数的图象由函数的图象向左平移个单位长度得到，则的图象与直线的交点个数为（ ）
A. 1B. 2C. 3D. 4
2. （2023全国乙卷10）已知函数在区间单调递增，直线和为函数的图像的两条相邻对称轴，则（ ）
A. B. C. D.
3.（2023全国Ⅰ卷15） 已知函数在区间有且仅有3个零点，则的取值范围是________．
4. （2023全国Ⅱ卷16）已知函数，如图A，B是直线与曲线的两个交点，若，则______．

5. （2023北京卷17）设函数．
（1）若，求的值．
（2）已知在区间上单调递增，，再从条件①、条件②、条件③这三个条件中选择一个作为已知，使函数存在，求的值．
条件①：；
条件②：；
条件③：在区间上单调递减．
注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
→➌模拟精练←
1．（2023·重庆·统考三模）将函数的图象向右平移个单位得到函数的图象，则“”是“函数为偶函数”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
2．（2023·江苏常州·江苏省前黄高级中学校考二模）将函数的图象向右平移个单位长度后得到函数的图象．若是函数的一个极值点，则的值为（ ）
A．B．C．D．
3．（多选）（2023·安徽黄山·统考三模）将函数的图象向左平移个单位后，得到函数的图象，则（ ）
A．函数存在一个极值点
B．函数的图象关于点对称
C．函数在区间上单调递增
D．函数在区间上有两个零点
4．（多选）（2023·河北唐山·统考三模）为了得到函数的图象，只需把余弦曲线上所有的点（ ）
A．横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移
B．横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移
C．向右平移，再把得到的曲线上各点横坐标缩短到原来的倍，纵坐标不变
D．向右平移，再把得到的曲线上各点横坐标缩短到原来的倍，纵坐标不变
5．（多选）（2023·湖南郴州·统考三模）设函数向左平移个单位长度得到函数，已知在上有且只有5个零点，则下列结论正确的是（ ）
A．的图象关于点对称
B．在上有且只有5个极值点
C．在上单调递增
D．的取值范围是
6．（2023·江苏·二模）已知函数的最小正周期为，若将其图象向右平移个单位长度后关于轴对称，则的解析式可能为（ ）
A．B．
C．D．
7．（2023·江苏南通·三模）将函数的图象向右平移个单位长度，得到的函数的图象关于点对称，且在区间上单调递增，则__________,实数m的取值范围是__________.
8．（2023·江苏南京·统考二模）已知，．
(1)若函数图象的两条相邻对称轴之间的距离为，求的值；
(2)若函数的图象关于对称，且函数在上单调，求的值．
→➍专题训练←
1.将函数的图象向左平移个单位长度，得到的图象的函数解析式为（ ）
A．B．
C．D．
2. 已知函数的图像经过点，且的相邻两个零点的距离为，为得到的图像，可将图像上所有点（ ）
A．先向右平移个单位，再将所得图像上所有点的横坐标缩短为原来的，纵坐标不变
B．先向左平移个单位，再将所得图像上所有点的横坐标缩短为原来的，纵坐标不变
C．先向左平移个单位，再将所得图像上所有点的横坐标伸长为原来的2倍，纵坐标不变
D．先向右平移个单位，再将所得图像上所有点的横坐标伸长为原来的2倍，纵坐标不变
3. 已知函数的定义域为，值域为，则的值不可能是( )
A．B．C．D．
4．已知函数的图象是由函数的图象向右平移个单位得到，则（ ）
A．的最小正周期为π
B．在区间上单调递增
C．的图象关于直线对称
D．的图象关于点对称
5．已知函数.
(1)求的最小正周期及对称轴方程；
(2)时，的最大值为，最小值为，求，的值.
6．（2023·广东揭阳·校考模拟预测）已知函数
(1)当，求的取值范围；
(2)已知锐角的内角A，B，C的对边分别为a，b，c，且，，求面积的最大值．
命题解读
命题预测
复习建议
函数的图象和性质是高考的热点，高考中多以中档题为主，常常与三角函数式的求值、化简相结合。出题的形式多样，主要考察图形的变换，以及看图，用图的能力，有一定的综合性。
预计2024年的函数的图象和性质及三角函数应用，仍然是出题的热点，必有题目考察这方面的知识，因此对于图象的掌握要到位，要学会看图、用图解题。
集合复习策略：
1.掌握函数的图象和性质，了解参数变化对函数的影响；
2.会运用三角函数解决简单的实际问题，会建立三角函数模型。
振幅
周期
频率
相位
初相
y=Asin(ωx+φ)
(A>0,ω>0),
A
T=
f==
ωx+φ
φ
x
ωx+φ
0
π
2π
y=Asin(ωx+φ)
0
A
0
-A
0