苏科版（2024）九年级上册2.4 圆周角一等奖课件ppt

这是一份苏科版（2024）九年级上册2.4 圆周角一等奖课件ppt，共31页。PPT课件主要包含了圆周角定理的推论等内容，欢迎下载使用。
1.进一步认识同弧（或等弧）所对的圆周角和圆心角之间的关系；2.掌握直径与其所对圆周角之间的关系.
如图，现在只有一个直角三角板，你能确定圆形笑脸的圆心吗？
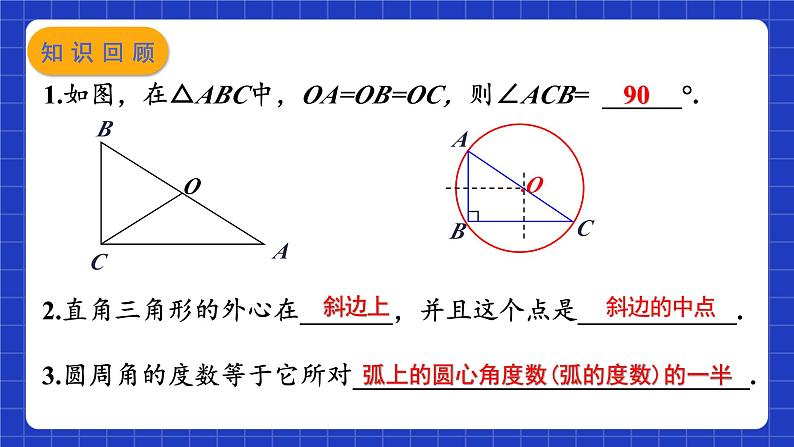
1.如图，在△ABC中，OA=OB=OC，则∠ACB= ______°.
2.直角三角形的外心在_______，并且这个点是____________.
3.圆周角的度数等于它所对______________________________.
弧上的圆心角度数(弧的度数)的一半
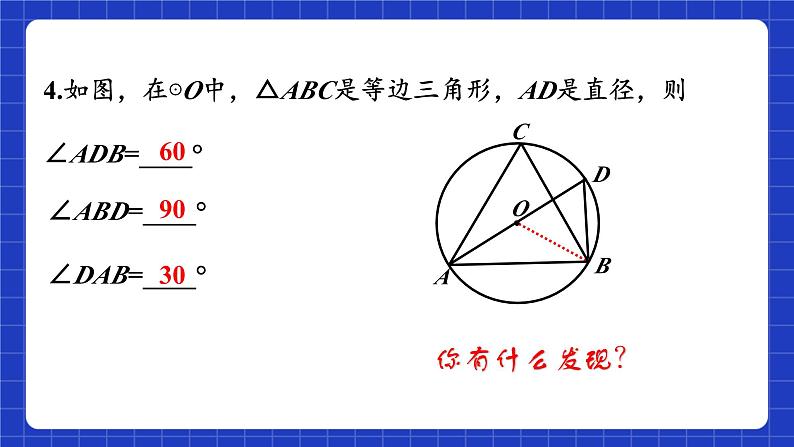
∠ABD=____°
4.如图，在⊙O中，△ABC是等边三角形，AD是直径，则∠ADB=____°
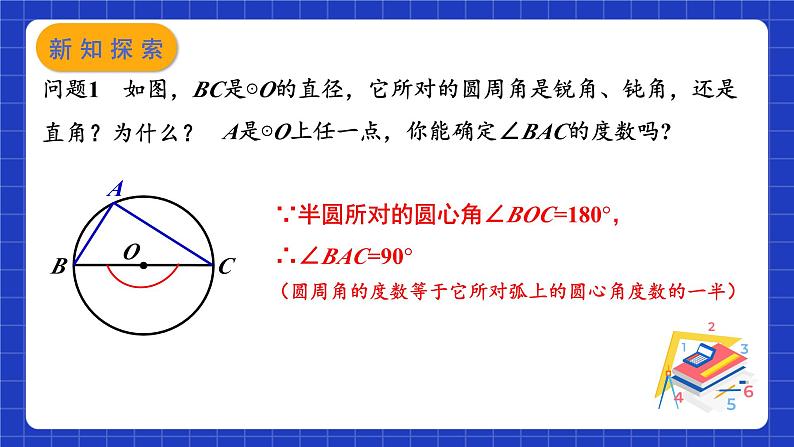
问题1　如图，BC是⊙O的直径，它所对的圆周角是锐角、钝角，还是直角？为什么？
A是⊙O上任一点，你能确定∠BAC的度数吗?
∵半圆所对的圆心角∠BOC=180°，∴∠BAC=90°
（圆周角的度数等于它所对弧上的圆心角度数的一半）
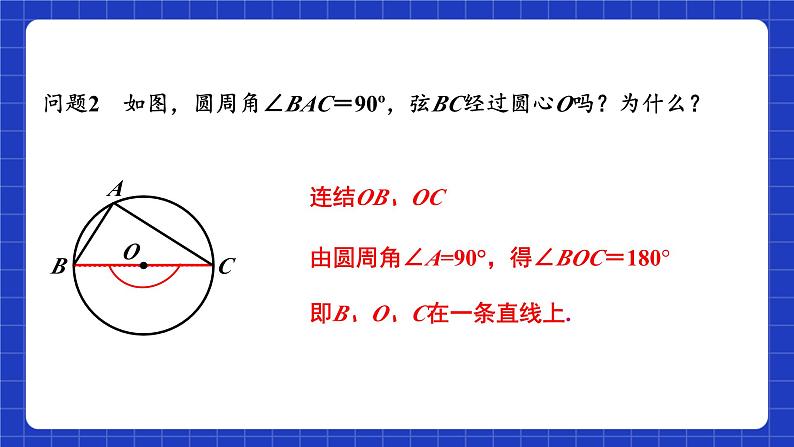
问题2　如图，圆周角∠BAC＝90º，弦BC经过圆心O吗？为什么？
由圆周角∠A=90°，得∠BOC＝180°即B、O、C在一条直线上.
半圆（或直径）所对的圆周角是直角；
用于判断某个圆周角是否是直角
用于判断某条弦是否是直径
90°的圆周角所对的弦是直径．
利用三角板在圆中画出两个90°的圆周角，这样就得到两条直径，那么这两条直径的交点就是圆心.
1.如图，△ABC的边AB是☉O的直径，D是BC的中点，(1)试判断△ABC的形状，并给出证明.
解： △ABC是等腰三角形证明如下：连接AD，∵AB是⊙O的直径，∴∠ADB＝90°， 即AD⊥BC.∵D是BC的中点，∴AD垂直平分BC，∴AB＝AC.∴ △ABC是等腰三角形
1.如图，△ABC的边AB是☉O的直径，D是BC的中点，(2)当△ABC为等边三角形时，点E是否为AC的中点？为什么？
解：(2)当△ABC为等边三角形时，E是AC的中点．理由如下：连接BE，∵AB为⊙O的直径，∴∠BEA＝90°，即BE⊥AC.∵△ABC为正三角形，∴AE＝EC，即E是AC的中点．
例1　如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，∠ADC=50°,求∠CEB的度数.
∵AB是⊙O的直径，∴∠ADB=90°(直径所对的圆周角是直角).∵∠ADC＝50°，∴∠EDB=∠ADB-∠ADC=90°-50°=40°.又∵∠ ABD=∠ACD=60° (同弧所对的圆周角相等)∴ ∠CEB=∠ABD+∠EDB=60°+40°=100°
解：(1)∠ACB与∠BAD相等，理由是：∵BC是⊙O的直径，∴∠BAC=90 °(直径所对的圆周角是直角). ，∴∠ACB+∠ABC=90°，∵AD⊥BC，∴∠BAD+∠ABC=90°，∴∠ACB=∠BAD
例2 已知：BC是⊙O的直径，A是⊙O上一点，AD⊥BC，垂足为D，
BE分别交AD、 AC于点F、G，
(2)判断△FAB的形状，并说明理由．
(3)图中是否还存在其他的等腰三角形？
解：(3)△FAG是等腰三角形，理由是： 由(2)得∠BAD=∠ABE ∵∠BAC=90 °(已证)，∴∠BAD+∠FAG=90°， ∠ABE+∠AGF=90°，∴ ∠FAG= ∠AGF.∴△FAG是等腰三角形.
变式1 在例2中，若点E与点A在直径BC的两侧，BE交AD的延长线于点F，其余条件不变（如下图）
(1)∠ACB与∠BAD还相等吗？ 为什么？(2)判断△FAB的形状，并说明理由．
变式2 A、B、E、C四点都在⊙O上，AD是△ABC的高，∠CAE＝∠BAD，AE是⊙O的直径吗？为什么？
1.遇到圆周角是90°，一般情况下联想到其所对的弦是直径，构造直角三角形；
2.利用直径所对的圆周角是直角可以解决角(两锐角之和为90°)、边(勾股定理)等问题．
1.“直径所对的角是直角”这种说法正确吗？
2.“90°的角所对的弦是直径”这种说法正确吗？
1. 用一块直角三角尺确定一个圆的圆心的位置，至少要用( )
A. 1次 B. 2次 C. 3次 D. 4次
2.如图，BC是⊙O的直径，点A是⊙O上异于B、C的一点，则∠A的度数为(　　)A．60° B．70° C．80° D．90°
3. BD是⊙O的直径，∠A＝60°，则∠DBC的度数是(　　)　
A．30° B．45° C．60° D．25°
解：∵BD是⊙O的直径，∴∠BCD＝90°.∵∠D＝∠A＝60°，∴∠DBC＝90°－∠D＝30°.
4.如图, 点A、B、C、D在☉O上, AC⊥BC, AC＝4, ∠ADC＝30°,则BC的长为( )
6.如图，点A、B、C在☉O上，BC∥OA，连接BO并延长，交☉O于点D，连接AC、DC.若∠A＝25°，则∠D的度数为 　40°⁠. 
7. 如图，△ABC内接于一圆，∠CAB＝30°，∠B＝60°，O是AB的中点，CD⊥AB于点E，交圆于点D.
(1)求证：点O是圆心；
解：(1)∵ ∠CAB＝30°，∠B＝60°，∴ ∠ACB＝180°－∠CAB－∠B＝90°.又∵ A、B两点都在圆上，∴ AB是圆的直径.又∵ O是AB的中点，∴ 点O是圆心.
(2) 求∠DAE的度数.
8.如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E，连接BD.
(1)求证：DE＝DB；
(2)若∠BAC＝90°，BD＝4，求△ABC外接圆的半径.