苏科版（2024）九年级上册4.2 等可能条件下的概率（一）优质课件ppt

这是一份苏科版（2024）九年级上册4.2 等可能条件下的概率（一）优质课件ppt，共24页。PPT课件主要包含了学习目标，知识回顾，有限的，一样大，思考与探索，共5种可能结果，有限性，等可能性，新知归纳，新知巩固等内容，欢迎下载使用。
1.在具体情境中进一步理解概率的意义，体会概率是描述随机现象的模型；
2.理解等可能条件下的概率（古典概型）的两个基本特征，会利用等可能条件下的概率计算公式求概率.
一般地， 设一个试验的所有可能发生的结果有n个，它们都是随机事件，每次试验有且只有其中一个结果出现. 如果每个结果出现的机会均等，那么我们说这n个事件的发生是等可能的，也称这个试验的结果具有等可能性.
1. 抛掷一枚质地均匀的骰子1次.
（1）点数朝上的试验结果是有限的还是无限的？
（2）如果有限的，共会出现多少种可能的情况？
（3）哪一个点数朝上的可能性较大？
（4）出现“朝上一面的点数大于4”与“朝上一面的点数不大于4”这两个事件发生中，哪个事件发生的可能性大？
当朝上一面的点数是5或6时，“朝上一面的点数大于4”这一事件(记为事件A)才能发生，于是事件A发生的概率
所以“朝上一面的点数不大于4”的可能性大.
当朝上一面的点数是1、2、3、4之一时，“朝上一面的点数不大于4”这一事件(记为事件B)才能发生，于是事件B发生的概率
2. 甲袋中装有5个相同的小球，它们分别写有1、2、3、4、5，从口袋中随机地取出1个小球，
（1）出现的结果是有限的还是无限的？
（3）取出写有哪个数字编号的小球的可能性较大？
（4）“编号是奇数”与“编号是偶数”这两个事件中，哪个事件发生的可能性大呢？
当取出的小球写有数字编号1、3、5时，“编号是奇数”这一事件(记为事件A)才能发生，于是事件A发生的概率
所以“编号是奇数”的可能性大.
当取出的小球写有数字编号2、4时，“编号是偶数”这一事件(记为事件B)才能发生，于是事件B发生的概率
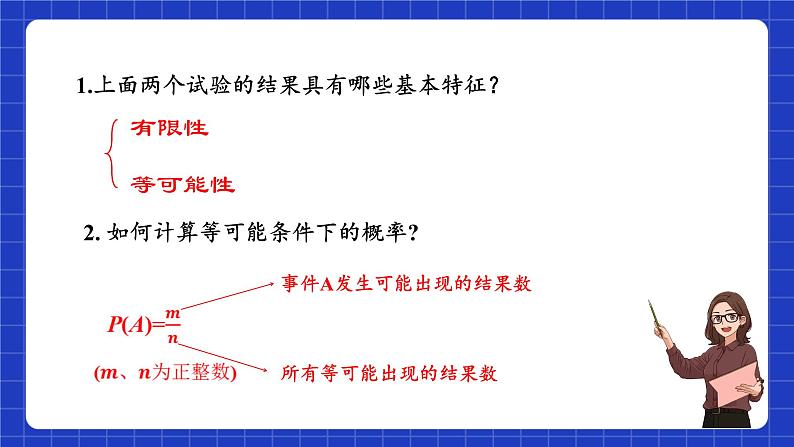
1.上面两个试验的结果具有哪些基本特征？
2. 如何计算等可能条件下的概率?
事件A发生可能出现的结果数
所有等可能出现的结果数
一般地，如果一个试验有n个等可能的结果，当其中的m个结果之一出现时，事件A发生，那么事件A发生的概率
例1 某班级有21名男生和19名女生，名字彼此不同．现有相同的40张小纸条，每名学生分别将自己的名字写在纸条上，放入一个盒子中，搅匀后从中抽出1张纸条．比较“抽到男生名字”与“抽到女生名字”的概率的大小．
解：全班40名学生中，每一名学生的名字被抽到的可能性是相同的.
所以“抽到男生名字”的概率大.
例2 一只不透明的袋子中装有3个白球和2个红球．这些球除颜色外都相同，拌匀后从中任意摸出1个球．
（1）会出现哪些等可能的结果？
（2）摸到白球、摸到红球的概率各是多少？
解：分别给5个球编上号码1、2、3、4、5，搅匀后任意摸出一个球，可能出现5种结果：1号球、2号球、3号球、4号球、5号球.这5种结果出现是等可能的.
1. 一道选择题有A、B、C、D四个选项，其中有且只有一个正确的选项，随意在A、B、C、D中选择一个答案，恰好正确的概率是_____.
2. 袋子中装有3个白球和7个红球，这些球除颜色外都相同，搅匀后从袋子中任意摸出1个球. P(摸到白球)＝____，P(摸到红球)＝____， P(摸到绿球)＝___，P(摸到白球或红球)＝____；
(1)P(A)=1，表示事件A一定发生;(2)P(A)=0，表示事件A一定不会发生;(3)0