专题05 函数类型的识别与应用模型构建（讲义）-2025年高考数学二轮复习讲练（新高考通用）

这是一份专题05 函数类型的识别与应用模型构建（讲义）-2025年高考数学二轮复习讲练（新高考通用），文件包含专题05函数类型的识别与应用模型构建讲义-2025年高考数学二轮复习讲练新高考通用原卷版docx、专题05函数类型的识别与应用模型构建讲义-2025年高考数学二轮复习讲练新高考通用解析版docx等2份试卷配套教学资源，其中试卷共68页， 欢迎下载使用。
\l "_Tc185866364" 01考情透视·目标导航 PAGEREF _Tc185866364 \h 2
\l "_Tc185866365" 02知识导图·思维引航 PAGEREF _Tc185866365 \h 3
\l "_Tc185866366" 03 知识梳理·方法技巧 PAGEREF _Tc185866366 \h 4
\l "_Tc185866367" 04 真题研析·精准预测 PAGEREF _Tc185866367 \h 5
\l "_Tc185866368" 05 核心精讲·题型突破 PAGEREF _Tc185866368 \h 12
\l "_Tc185866369" 题型一：二次函数与幂模型 PAGEREF _Tc185866369 \h 12
\l "_Tc185866370" 题型二：分段函数模型 PAGEREF _Tc185866370 \h 19
\l "_Tc185866371" 题型三：对勾函数模型 PAGEREF _Tc185866371 \h 23
\l "_Tc185866372" 题型四：指数函数模型 PAGEREF _Tc185866372 \h 29
\l "_Tc185866373" 题型五：对数函数模型 PAGEREF _Tc185866373 \h 34
\l "_Tc185866374" 重难点突破：函数模型的选择 PAGEREF _Tc185866374 \h 39
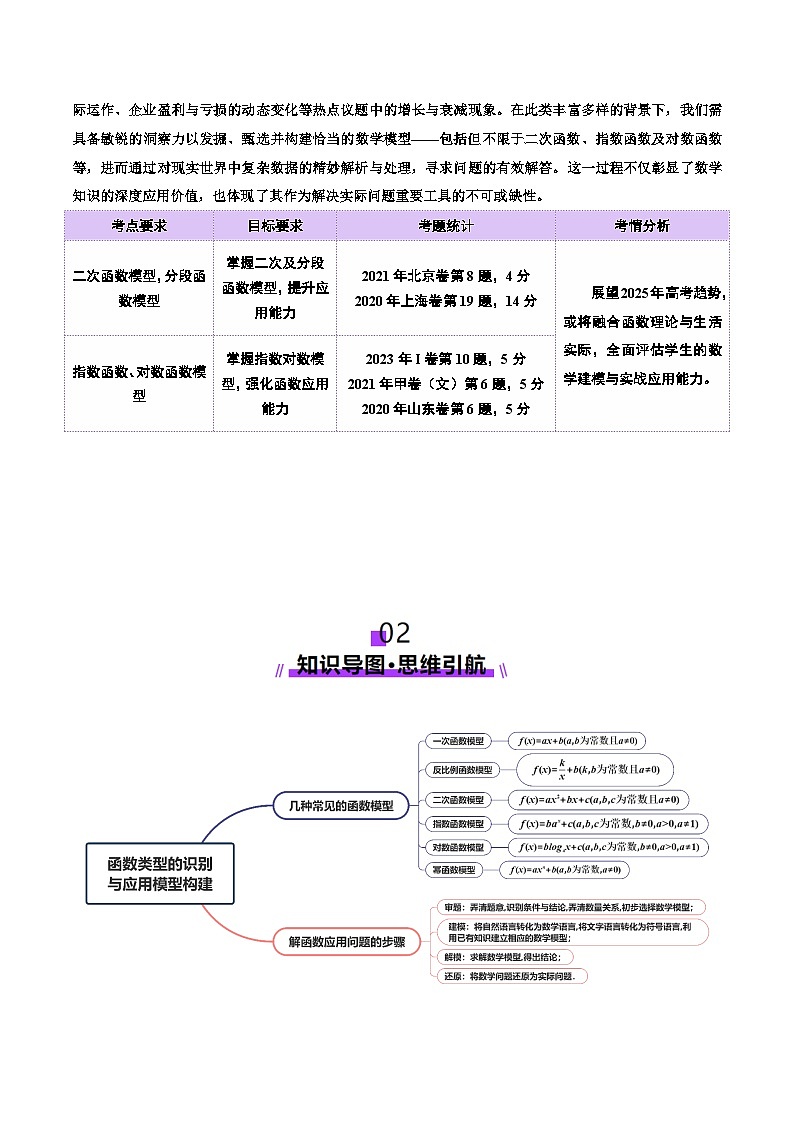
本节内容倾向于采纳跨学科视角或植根于社会生活的实际场景来构建命题，诸如聚焦于生产经营的实际运作、企业盈利与亏损的动态变化等热点议题中的增长与衰减现象。在此类丰富多样的背景下，我们需具备敏锐的洞察力以发掘、甄选并构建恰当的数学模型——包括但不限于二次函数、指数函数及对数函数等，进而通过对现实世界中复杂数据的精妙解析与处理，寻求问题的有效解答。这一过程不仅彰显了数学知识的深度应用价值，也体现了其作为解决实际问题重要工具的不可或缺性。
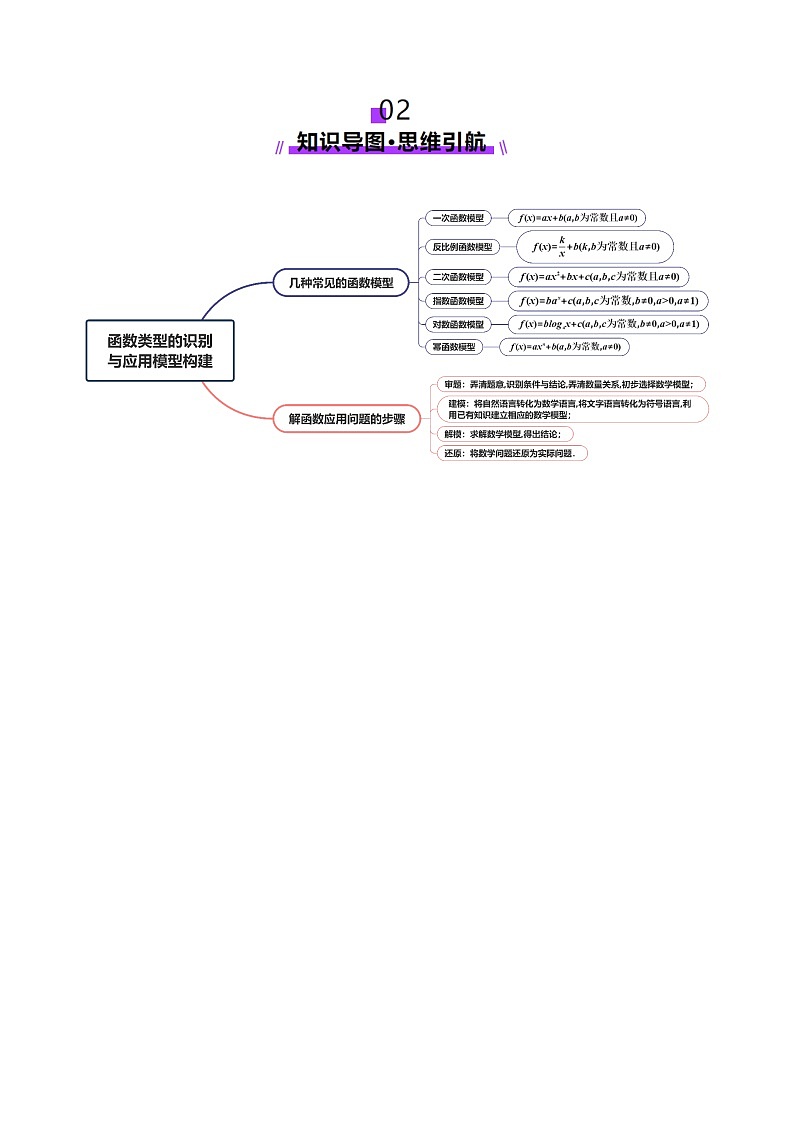
1、几种常见的函数模型：
2、解函数应用问题的步骤：
（1）审题：弄清题意，识别条件与结论，弄清数量关系，初步选择数学模型；
（2）建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用已有知识建立相应的数学模型；
（3）解模：求解数学模型，得出结论；
（4）还原：将数学问题还原为实际问题．
3、解答函数应用题应注意的问题
首先，要认真阅读理解材料．应用题所用的数学语言多为“文字语言、符号语言、图形语言”并用，往往篇幅较长，立意有创新脱俗之感．阅读理解材料要达到的目标是读懂题目所叙述的实际问题的意义，领悟其中的数学本质，接受题目所约定的临时性定义，理解题目中的量与量的位置关系、数量关系，确立解体思路和下一步的努力方向，对于有些数量关系较复杂、较模糊的问题，可以借助画图和列表来理清它．
其次，建立函数关系．根据前面审题及分析，把实际问题“用字母符号、关系符号”表达出来，建立函数关系．
其中，认真阅读理解材料是建立函数模型的关键．在阅读这一过程中应像解答语文和外语中的阅读问题一样，有“泛读”与“精读”之分．这是因为一般的应用问题，一方面为了描述的问题与客观实际尽可能地相吻合，就必须用一定的篇幅描述其中的情境；另一方面有时为了思想教育方面的需要，也要用一些非数量关系的语言来叙述，而我们解决问题所关心的东西是数量关系，因此对那些叙述的部分只需要“泛读”即可．反过来，对那些刻画数量关系、位置关系、对应关系等与数学有关的问题的部分，则应“精读”，一遍不行再来一遍，直到透彻地理解为止，此时切忌草率．
1．（多选题）（2023•新高考Ⅰ）噪声污染问题越来越受到重视．用声压级来度量声音的强弱，定义声压级，其中常数是听觉下限阈值，是实际声压．下表为不同声源的声压级：
已知在距离燃油汽车、混合动力汽车、电动汽车处测得实际声压分别为，，，则
A．B．C．D．
【答案】
【解析】由题意得，，，
，，
，，
可得，正确；
，错误；
，正确；
，，正确．
故选：．
2．（2023•上海）为了节能环保、节约材料，定义建筑物的“体形系数” ，其中为建筑物暴露在空气中的面积（单位：平方米），为建筑物的体积（单位：立方米）．
（1）若有一个圆柱体建筑的底面半径为，高度为，暴露在空气中的部分为上底面和侧面，试求该建筑体的“体形系数” ；（结果用含、的代数式表示）
（2）定义建筑物的“形状因子”为，其中为建筑物底面面积，为建筑物底面周长，又定义为总建筑面积，即为每层建筑面积之和（每层建筑面积为每一层的底面面积）．设为某宿舍楼的层数，层高为3米，则可以推导出该宿舍楼的“体形系数”为．当，时，试求当该宿舍楼的层数为多少时，“体形系数” 最小．
【解析】（1）由圆柱体的表面积和体积公式可得：
，
所以．
（2）由题意可得，，
所以，
令，解得，
所以在，单调递减，在，单调递增，
所以的最小值在或7取得，
当时，，
当时，，
所以在时，该建筑体最小．
3．（2021•甲卷）青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据和小数记录法的数据满足．已知某同学视力的五分记录法的数据为4．9，则其视力的小数记录法的数据约为
A．1．5B．1．2C．0．8D．0．6
【答案】
【解析】在中，，所以，即，
解得，
所以其视力的小数记录法的数据约为0．8．
故选：．
4．（2021•北京）某一时段内，从天空降落到地面上的雨水，未经蒸发、渗漏、流失而在水平面上积聚的深度，称为这个时段的降雨量（单位：．24 降雨量的等级划分如下：
在综合实践活动中，某小组自制了一个底面直径为，高为的圆锥形雨量器．若一次降雨过程中，该雨量器收集的的雨水高度是 如图所示），则这降雨量的等级是
A．小雨B．中雨C．大雨D．暴雨
【答案】
【解析】圆锥的体积为，
因为圆锥内积水的高度是圆锥总高度的一半，
所以圆锥内积水部分的半径为，
将，代入公式可得，
图上定义的是平地上积水的厚度，即平地上积水的高，
平底上积水的体积为，且对于这一块平地的面积，即为圆锥底面圆的面积，
所以，
则平地上积水的厚度，
因为，
由题意可知，这一天的雨水属于中雨．
故选：．
5．（2021•上海）已知一企业今年第一季度的营业额为1．1亿元，往后每个季度增加0．05亿元，第一季度的利润为0．16亿元，往后每一季度比前一季度增长．
（1）求今年起的前20个季度的总营业额；
（2）请问哪一季度的利润首次超过该季度营业额的？
【解析】（1）由题意可知，可将每个季度的营业额看作等差数列，
则首项，公差，
，
即营业额前20季度的和为31．5亿元．
（2）解法一：假设今年第一季度往后的第季度的利润首次超过该季度营业额的，
则，
令，，
即要解，
则当时，，
令，解得：，
即当时，递减；当时，递增，
由于（1），因此的解只能在时取得，
经检验，，，
所以今年第一季度往后的第25个季度的利润首次超过该季度营业额的．
解法二：设今年第一季度往后的第季度的利润与该季度营业额的比为，
则，
数列满足，
注意到，，，
今年第一季度往后的第25个季度利润首次超过该季度营业额的．
6．（2020•上海）在研究某市交通情况时，道路密度是指该路段上一定时间内通过的车辆数除以时间，车辆密度是该路段一定
时间内通过的车辆数除以该路段的长度，现定义交通流量为，为道路密度，为车辆密度，交通流量．
（1）若交通流量，求道路密度的取值范围；
（2）已知道路密度时，测得交通流量，求车辆密度的最大值．
【解析】（1）按实际情况而言，交通流量随着道路密度的增大而减小，
故是单调递减函数，
所以，
当时，最大为85，
于是只需令，解得，
故道路密度的取值范围为．
（2）把，代入中，
得，解得．
，
①当时，，
．
②当时，是关于的二次函数，，
对称轴为，此时有最大值，为．
综上所述，车辆密度的最大值为．
7．（2020•山东）基本再生数与世代间隔是新冠肺炎的流行病学基本参数．基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型：描述累计感染病例数随时间（单位：天）的变化规律，指数增长率与，近似满足．有学者基于已有数据估计出，．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为
A．1．2天B．1．8天C．2．5天D．3．5天
【答案】
【解析】把，代入，可得，，
当时，，则，
两边取对数得，解得．
故选：．
8．（2019•新课标Ⅱ）2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就．实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系．为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日点的轨道运行．点是平衡点，位于地月连线的延长线上．设地球质量为，月球质量为，地月距离为，点到月球的距离为，根据牛顿运动定律和万有引力定律，满足方程：．
设．由于的值很小，因此在近似计算中，则的近似值为
A．B．C．D．
【答案】
【解析】．，
满足方程：．
，
把代入，得：，
，
，
．
故选：．
9．（2018•浙江）我国古代数学著作《张邱建算经》中记载百鸡问题：“今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一．凡百钱，买鸡百只，问鸡翁、母、雏各几何？”设鸡翁，鸡母，鸡雏个数分别为，，，则，当时， ， ．
【答案】8；11
【解析】，当时，化为：，
解得，．
故答案为：8；11．
题型一：二次函数与幂模型
【典例1-1】红星幼儿园要建一个长方形露天活动区，活动区的一面利用房屋边墙（墙长），其它三面用某种环保材料围建，但要开一扇宽的进出口（不需材料），共用该种环保材料，则可围成该活动区的最大面积为（ ）
A．B．C．D．
【答案】C
【解析】设这个活动区垂直于墙的一边长是，则平行于墙的一边是，
面积，
墙长，所以，
解得，
对称轴方程，
抛物线开口向下，，函数在上递减，
当时，最大为（），
故选：C．
【典例1-2】某厂以x千克/小时的速度匀速生产某种产品（生产条件要求），每小时可获得利润元，要使生产100千克该产品获得的利润最大，该厂应选取的生产速度是（ ）
A．2千克/小时B．3千克/小时
C．4千克/小时D．6千克/小时
【答案】C
【解析】由题意得，生产100千克该产品获得的利润为，，
令，，则，故当时，最大，此时.
故选：C
【变式1-1】[新考法]（2024·河南新乡·三模）下列集合中有无数个元素的是（ ）
A．x∈N4x∈NB．x∈Z4x∈NC．x∈N4x∈ZD．x∈Q4x∈N
1、二次函数模型的应用
构建二次函数模型解决最优问题时，可以利用配方法、判别式法、换元法、讨论函数的单调性等方法求最值，也可以根据函数图象的对称轴与函数定义域的对应区间之间的位置关系讨论求解，但一定要注意自变量的取值范围．
2、幂函数模型为（，为常数，），
在计算幂函数解析式、求幂函数最值的时候，通常利用幂函数图像、单调性、奇偶性解题．
【变式1-2】（2024·黑龙江哈尔滨·三模）如图为某小区七人足球场的平面示意图，为球门，在某次小区居民友谊比赛中，队员甲在中线上距离边线米的点处接球，此时，假设甲沿着平行边线的方向向前带球，并准备在点处射门，为获得最佳的射门角度（即最大），则射门时甲离上方端线的距离为（ ）
A．B．C．D．
【答案】B
【解析】设，并根据题意作如下示意图，由图和题意得：，，
所以，且，
所以，
又，所以，解得，即，
设，，则，
，所以在中，
有，
令，所以，
所以，
因为，所以，则要使最大，
即要取得最小值，即取得最大值，
即在取得最大值，
令， ，
所以的对称轴为：，所以在单调递增，在单调递减，
所以当时，取得最大值，即最大，此时，即，
所以，所以，即为获得最佳的射门角度（即最大），
则射门时甲离上方端线的距离为：.
故选：B.
【变式1-3】在国家大力推广新能源汽车的背景下，各大车企纷纷加大对新能源汽车的研发投入，某车企研发部有100名研发人员，原年人均投入40万元，现准备将这100名研发人员分成两部分：燃油车研发部和新能源车研发部，其中燃油车研发部有x名研究人员，调整后新能源车研发部的年人均投入比原来增加，而燃油车研发部的年人均投入调整为万元.
(1)若要使新能源车研发部的年总投入不低于调整前原100名研发人员的年总投入，求调整后新能源车研发人员最少为多少人？
(2)若要使新能源车研发部的年总投入始终不低于燃油车研发部的年总投入，求正整数m的最大值.
【解析】（1）令新能源车研发部的年总投入，
则，
令，则，
∵，∴，
故调整后新能源车研发人员最少为34人
（2）令燃油车研发部的年总投入
则，
即在恒成立.
令，即在上恒成立，
，
是开口向上的二次函数，∵
①对称轴时，即，时在上恒成立；
②当对称轴时，即，，解得
综上所述：
∴的最大值为：6.
1．（2024·上海崇明·一模）某公园有一块如图所示的区域，该场地由线段、、及曲线段围成.经测量， ，米，曲线是以为对称轴的抛物线的一部分，点到、的距离都是50米.现拟在该区域建设一个矩形游乐场，其中点在曲线段上，点、分别在线段、上，且该游乐场最短边长不低于30米.设米，游乐场的面积为平方米.

(1)试建立平面直角坐标系，求曲线段的方程；
(2)求面积关于的函数解析式；
(3)试确定点的位置，使得游乐场的面积最大.
【解析】（1）以为坐标原点，、所在直线分别为轴、轴建立平面直角坐标系，
如图所示，则，，，
设曲线所在的抛物线方程为，，点，在抛物线上，
则，解得，，
所以曲线段所在的抛物线方程为.
（2）因为点在曲线段上，，，所以，
∴，.
（3）∵，，
令，解得，
当时，f'x>0，当时，f'x，此时用来拟合上述表格中的数据更好；
当或时，=，用拟合效果一样；
当或时，