初中数学湘教版（2024）八年级下册第1章 直角三角形1.4 角平分线的性质精品课件ppt

这是一份初中数学湘教版（2024）八年级下册第1章 直角三角形1.4 角平分线的性质精品课件ppt，共21页。PPT课件主要包含了角的平分线的性质，书写格式，归纳总结，应满足的条件，你能证明这个结论吗等内容，欢迎下载使用。
会应用角的平分线的性质定理的逆定理解决相关问题（难点）.
掌握角的平分线的性质定理的逆定理（重点）.
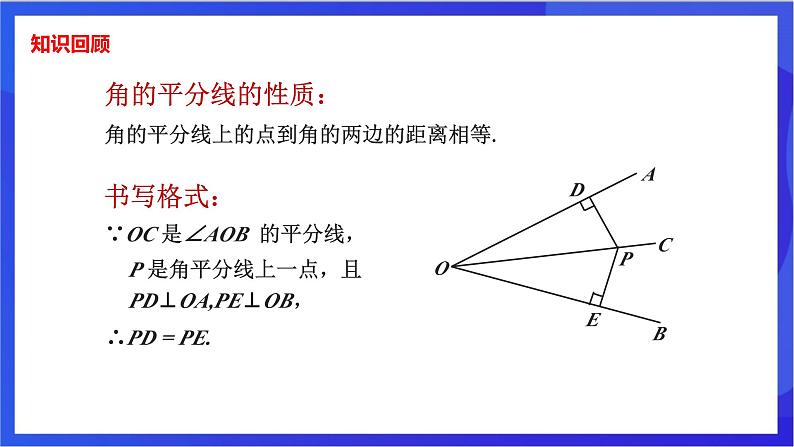
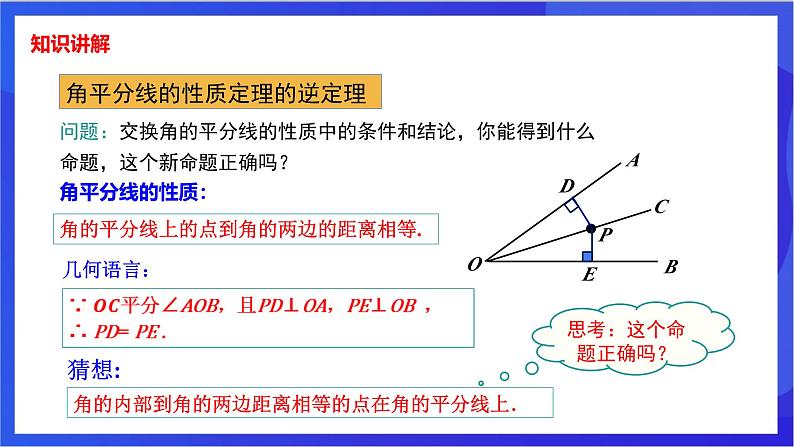
角的平分线上的点到角的两边的距离相等.
∵OC 是∠AOB 的平分线，
P 是角平分线上一点，且PD⊥OA,PE⊥OB，
角的内部到角的两边距离相等的点在角的平分线上．
问题：交换角的平分线的性质中的条件和结论，你能得到什么命题，这个新命题正确吗？
思考：这个命题正确吗？
角平分线的性质定理的逆定理
证明猜想已知：如图，PD⊥OA，PE⊥OB，垂足分别是D、E，PD=PE.求证：点P 在∠AOB 的平分线上.
∴点P 在∠AOB 的平分线上.
在Rt△PDO 和Rt△PEO 中，
（全等三角形的对应角相等）.
∵PD⊥OA,PE⊥OB ,
∴Rt△PDO≌Rt△PEO（HL）.
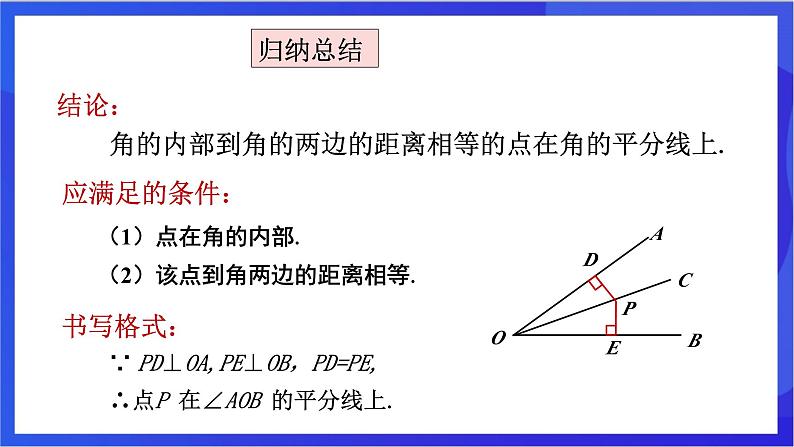
结论： 角的内部到角的两边的距离相等的点在角的平分线上.
∵ PD⊥OA,PE⊥OB，PD=PE,
∴点P 在∠AOB 的平分线上.
如图，在△ABC 中，D 是BC 的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，且BE＝CF.求证：AD 是△ABC 的角平分线.
证明：∵DE⊥AB，DF⊥AC, ∴∠BED =∠CFD =90°. ∵D 是BC 的中点, ∴BD =CD. 在Rt△BED 和Rt△CFD 中，
∴Rt△BED ≌Rt△CFD（HL）,
∴∠BAD=∠CAD,
∴AD 是△ABC 的角平分线.
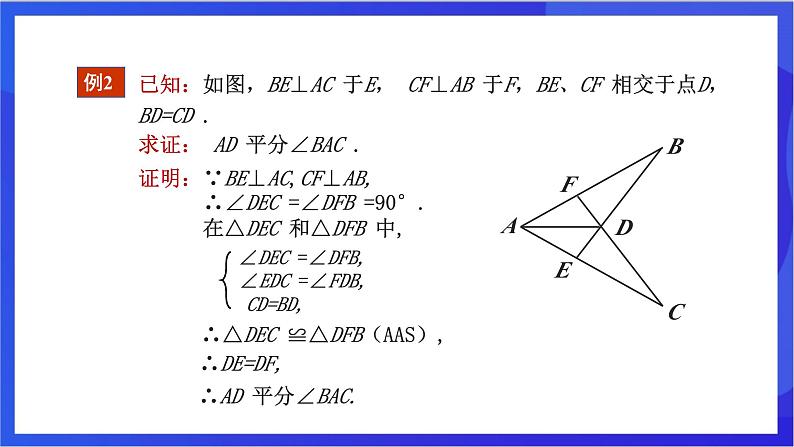
已知：如图，BE⊥AC 于E， CF⊥AB 于F，BE、CF 相交于点D， BD=CD .求证： AD 平分∠BAC .
证明：∵BE⊥AC,CF⊥AB, ∴∠DEC =∠DFB =90°. 在△DEC 和△DFB 中,
∠DEC =∠DFB,
∠EDC =∠FDB,
∴△DEC ≌△DFB（AAS）,
∴DE=DF,
∴AD 平分∠BAC.
活动1 分别画出下列三角形三个内角的平分线，你发现了什么？
发现：三角形的三条角平分线相交于一点
活动2 分别过交点作三角形三边的垂线，用刻度尺量一量，每组垂线段，你发现了什么？
发现：过交点作三角形三边的垂线段相等
如图，△ABC的角平分线BM、CN相交于点P.求证：点P到三角形三边的距离均相等.
证明：过点P作PF 、PE、PG分别垂直于AB、 BC、CA，垂足分别为F、E、G,
∵BM是△ABC的角平分线，点P在BM上， ∴PF=PE.（在角平分线上的点到角的两边 的距离相等） 同理 PE=PG. ∴ PF=PE=PG. 即点P到边AB、BC、CA的距离相等.
结论：三角形的三条内角平分线交于一点，并且这点到三边的距离相等.
A．110° B．120° C．130° D．140°
1. 如图，某个居民小区C附近有三条两两相交的道路MN、OA、OB，拟在MN上建造一个大型超市，使得它到OA、OB的距离相等，请确定该超市的位置P.
填空：(1) ∵∠1=∠2,DC⊥AC, DE⊥AB, ∴___________.( ______________________________________ )(2) ∵DC⊥AC ,DE⊥AB ,DC=DE, ∴____________________________________( ________________________________________________ )
∠1= ∠2（AD 是∠BAC 的角平分线）.
到一个角的两边的距离相等的点，在这个角平分线上.
在角平分线上的点到角的两边的距离相等.
3.如图所示，已知△ABC 中，PE∥AB 交BC 于点E，PF∥AC 交BC 于点F，点P 是AD上一点，且点D 到PE 的距离与到 PF 的距离相等，判断AD 是否平分∠BAC，并说明理由.
解：AD 平分∠BAC．理由如下： ∵D 到PE 的距离与到PF 的距离相等， ∴点D 在∠EPF 的平分线上. ∴∠1＝∠2． 又∵PE∥AB，∴∠1＝∠3． 同理，∠2＝∠4． ∴∠3＝∠4，∴AD 平分∠BAC.
4.如图，已知∠CBD 和∠BCE 的平分线相交于点F. 求证：点F 在∠DAE 的平分线上.
过点F 作FG⊥AE 于点G，FH⊥AD 于点H，FM⊥BC 于点M.
∵点F 在∠BCE 的平分线上， 　　　　FG⊥AE，FM⊥BC，
又∵点F 在∠CBD 的平分线上， 　　　　FH⊥AD，FM⊥BC，
∴点F在∠DAE的平分线上.　　　
5.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
角的平分线的性质定理的逆定理
1.内容：角的内部到角的两边的距离相等的点在角的平分线上.
2.作用：证明角相等，判定一条射线是角平分线.