初中数学湘教版（2024）八年级下册2.2.1平行四边形的性质完整版课件ppt

这是一份初中数学湘教版（2024）八年级下册2.2.1平行四边形的性质完整版课件ppt，共17页。PPT课件主要包含了平行四边形的定义，想一想，画一画，做一做，平行四边形的性质等内容，欢迎下载使用。
1.理解平行四边形的概念；2.探索并证明平行四边形的性质定理：平行四边形的对边相等、对角相等；（重点） 3.运用平行四边形的性质进行简单的计算和证明；（重、难点）4.经历“实验—猜想—验证—证明”的过程,发展思维水平.
你能找出图片中的平行四边形吗？
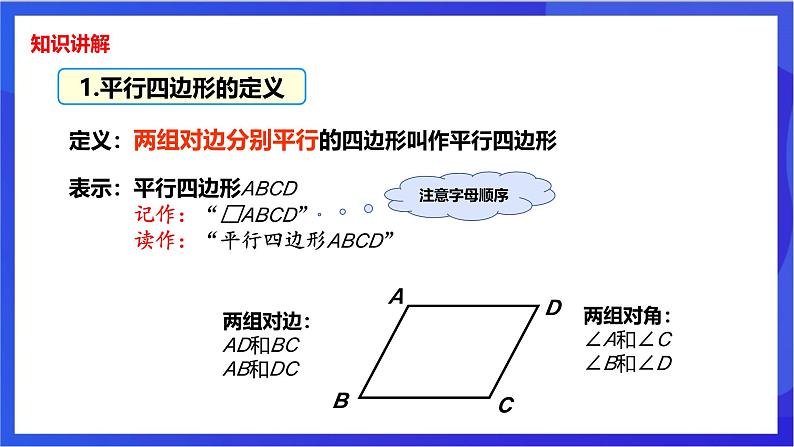
定义：两组对边分别平行的四边形叫作平行四边形
两组对边：AD和BCAB和DC
两组对角：∠A和∠C∠B和∠D
表示：平行四边形ABCD 记作：“□ABCD” 读作：“平行四边形ABCD”
平行四边形的对边之间、对角之间有怎样的数量关系?
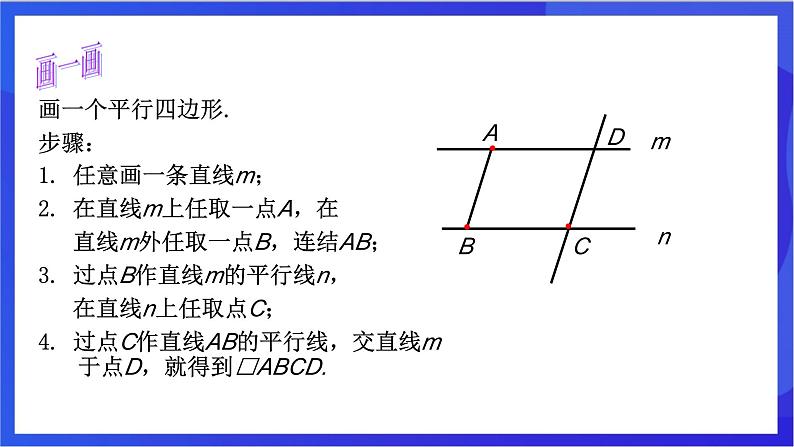
画一个平行四边形.步骤：1. 任意画一条直线m；2. 在直线m上任取一点A，在 直线m外任取一点B，连结AB；3. 过点B作直线m的平行线n， 在直线n上任取点C；4. 过点C作直线AB的平行线，交直线m于点D，就得到□ABCD.
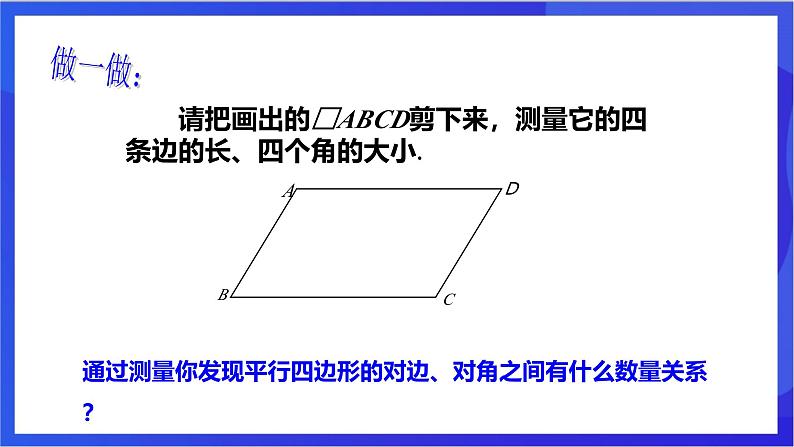
请把画出的□ABCD剪下来，测量它的四条边的长、四个角的大小.
通过测量你发现平行四边形的对边、对角之间有什么数量关系？
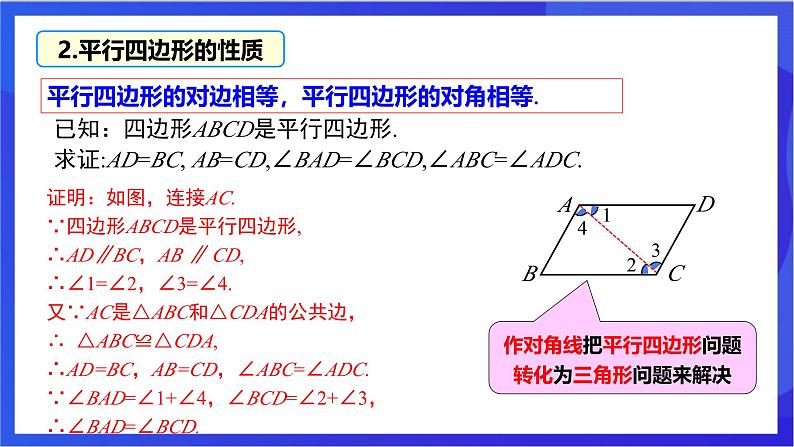
平行四边形的对边相等，平行四边形的对角相等.
作对角线把平行四边形问题转化为三角形问题来解决
已知：四边形ABCD是平行四边形.求证:AD=BC, AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证明：如图，连接AC.∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠1=∠2，∠3=∠4.又∵AC是△ABC和△CDA的公共边，∴ △ABC≌△CDA,∴AD=BC，AB=CD，∠ABC=∠ADC.∵∠BAD=∠1+∠4，∠BCD=∠2+∠3，∴∠BAD=∠BCD.
思考 不添加辅助线，你能否证明其对角相等？
证明：∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠A+∠B=180°，∠A+∠D=180°，∴∠B=∠D.同理可得∠A=∠C.
例1 如图,在 □ABCD中，已知∠A=40°，求其他各个内角的度数．
解 ∵四边形ABCD是平行四边形，∴ ∠C =∠A = 40°. ∵ AD∥BC， ∴ ∠B = 180°－∠A = 180° － 40° = 140°，∴ ∠D = ∠B = 140° .
变式1．已知： □ ABCD中， 若∠A＋∠C=80°，你能求出各角的度数吗？说说你的理由．变式2．已知： □ ABCD中， 若∠B＝2∠A ，你能求出各角的度数吗？说说你的理由．
例2 如图，在□ ABCD 中，AB=8，周长等于24.求其余三条边的长．
解: 在□ ABCD 中， AB=CD, AD=BC.∵ AB=8，∴ CD=8.又∵AB+BC+CD+AD=24， ∴ AD=BC=4.
变式1 如图：已知平行四边形ABCD周长等于16，AB：BC=3：5, 求平行四边形的各边长．变式2 如图：已知平行四边形ABCD，CD=3cm,BC=5cm,AC=4cm, 求□ ABCD的面积．
3.平行线间的平行线段
如图，直线l1与l2平行，AB、CD是l1与l2之间的任意两条平行线段，试问：AB与CD是否相等？为什么？
解：∵ l1 ∥ l2， AB ∥ CD， ∴四边形ABCD是平行四边形， ∴AB=CD.
结论：夹在两条平行线间的平行线段相等.
1.已知: □ABCD.（1） 若AB+BC=10，则□ ABCD的周长为 .（2） 若∠A+∠C=100°，则∠B=____，∠C=____.（3）若AD∶CD =3∶4，周长是42，则AB=____，BC=____.（4）∠A∶∠B∶∠C∶∠D的值可以是（ ） A. 1∶2∶3∶4 B. 1∶2∶2∶1 C. 1∶1∶2∶2 D. 2∶1∶2∶1（5）∠A：∠B=5:4，则∠C、∠D的度数分别为（ ） A. 100°和80° B. 100°和50° C. 120°和60° D. 135°和45°
证明： ∵四边形ABCD是平行四边形， ∴ AB∥CD，AD=BC.∴ ∠CDE= ∠DEA， ∠CFB= ∠FBA.又∵∠CDE= ∠ADE， ∠CBF= ∠FBA,∴ ∠DEA= ∠ADE，∠CFB=∠CBF,∴AE=AD, CF=BC, ∴AE= CF.
2.已知在平行四边形ABCD中，DE平分∠ADC,BF平分∠ABC.求证:AE=CF.
证明： ∵ 四边形BEFM是平行四边形,　 ∴BM=EF,AB//EF. ∵ AD平分∠BAC, ∴∠BAD=∠CAD. ∵AB//EF, ∴ ∠BAD=∠AEF, ∴∠CAD =∠AEF, ∴ AF=EF, ∴ AF=BM.
3.如图，在ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证：AF=BM.
夹在两条平行线之间的平行线段相等.