初中数学湘教版（2024）八年级下册2.2.2平行四边形的判定一等奖课件ppt

这是一份初中数学湘教版（2024）八年级下册2.2.2平行四边形的判定一等奖课件ppt，共20页。PPT课件主要包含了学习目标，复习导入，知识讲解，符号语言，∴AD∥BC，随堂练习，从边考虑，从角考虑，从对角线考虑，平行四边形的判定方法等内容，欢迎下载使用。
1.探索并证明“对角线互相平分的四边形是平行四边形”；（重点）2.应用平行四边形的判定定理解决问题.（难点）
问题1 除了两组对边分别平行，平行四边形还有哪些性质？
平行四边形的对角相等.
平行四边形的对角线互相平分.
思考 我们得到的这些逆命题是否都成立？这节课我们一起来 进行探讨.
问题2 上面的两条性质的逆命题各是什么？
两组对角分别相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
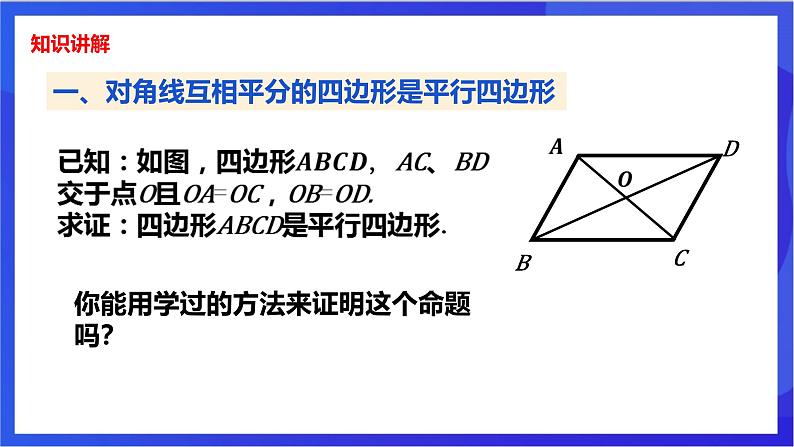
你能用学过的方法来证明这个命题吗？
一、对角线互相平分的四边形是平行四边形
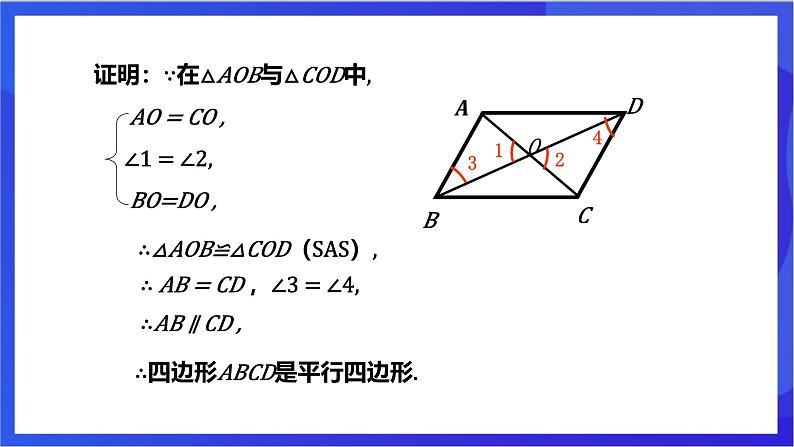
证明：∵在△AOB与△COD中, AO = CO , ∠1 = ∠2, BO=DO ,
∴△AOB≌△COD（SAS）,
∴ AB = CD ，∠3 = ∠4,
∴四边形ABCD是平行四边形.
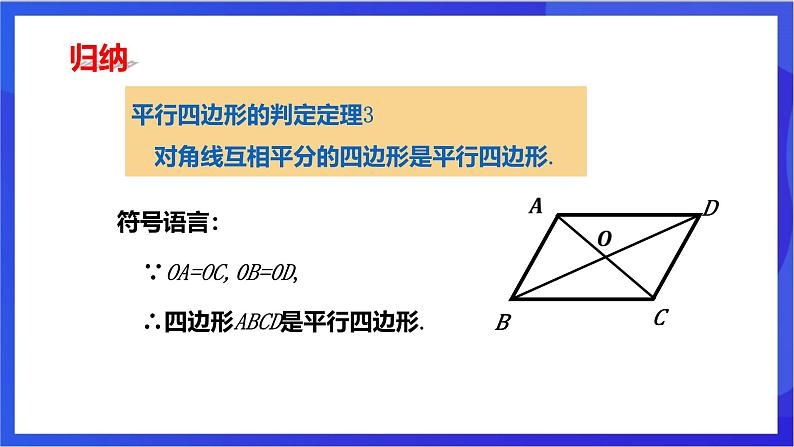
平行四边形的判定定理3 对角线互相平分的四边形是平行四边形.
∵OA=OC,0B=0D,
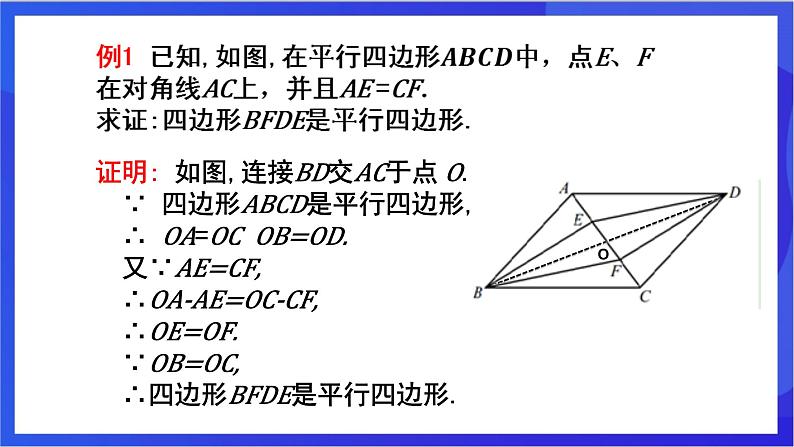
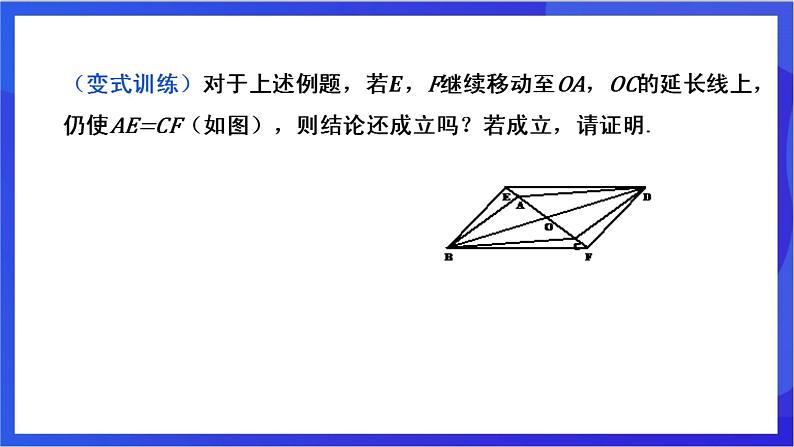
证明: 如图,连接BD交AC于点 O. ∵ 四边形ABCD是平行四边形, ∴ OA=OC OB=OD. 又∵AE=CF, ∴OA-AE=OC-CF, ∴OE=OF. ∵OB=OC, ∴四边形BFDE是平行四边形.
二、两组对角分别相等的四边形是平行四边形
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D，
∵∠A+∠C+∠B+∠D=360°，
∴2∠A+2∠B=360°，
即∠A+∠B=180°，
同理得 AB∥ CD，
平行四边形的判定定理：两组对角分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵∠A=∠C，∠B=∠D,∴四边形ABCD是平行四边形.
例2 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°，∴∠D＝180°－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB，∴∠DAB＝∠1＋∠2＝125°.∵∠DCB＋∠DAB＋∠D＋∠B＝360°，∴∠DCB＝∠DAB＝125°.又∵∠D＝∠B＝55°，∴四边形ABCD是平行四边形．
小明要做一个平行四边形木框.他要从图中几根木条中选出四根来制作，可是他不知道该怎样选，请同学们帮他选一选，哪四根木条可以制作成平行四边形木框，为什么？
发现：一组对边平行，另一组对边相等的四边形不一定是平行四边形.两组边相等四边形也不一定是平行四边形.
1．如图，在四边形ABCD中，AC、BD相交于点O，（1）若AD=8cm，AB=4cm，那么当BC=___  _cm，CD=___  _cm时，四边形ABCD为平行四边形； （2）若AC=8cm，BD=10cm，那么当AO=__  _cm，DO=__  _cm时，四边形ABCD为平行四边形．
2.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　）A．OA=OC，OB=OD B．AB=CD，AO=CO C．AB=CD，AD=BC D．∠BAD=∠BCD，AB∥CD
3.如图，AB、CD相交于点O，AC∥DB，AO＝BO，E、F分别是OC、OD的中点．求证：(1)△AOC≌△BOD；(2)四边形AFBE是平行四边形．
证明：(1)∵AC∥BD，∴∠C＝∠D.又∵∠COA=∠DOB，AO＝BO ，∴△AOC≌△BOD(AAS).(2)∵△AOC≌△BOD，∴CO＝DO.∵E、F分别是OC、OD的中点，∴EO＝FO.又∵AO＝BO，∴四边形AFBE是平行四边形．
4.如图，△ABC中，AB=AC=10，D是BC边上的任意一点，分别作DF∥AB交AC于F，DE∥AC交AB于E，求DE+DF的值．
解：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴DE=AF.又∵AB=AC=10，∴∠B=∠C.∵DF∥AB，∴∠CDF=∠B，∴∠CDF=∠C，∴DF=CF，∴DE+DF=AF+FC=AC=10．
解：(1)分别过点A,C作BC,BA的平行线,两平行线相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
5 如图所示,有一块平行四边形玻璃镜片,不小心打掉了一块,但是有两条边是完好的.同学们想想看,有没有办法把原来的平行四边形重新画出来?
(2)分别以点A,C为圆心,以BC,BA的长为半径画弧,两弧相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
（3）连接AC,取AC的中点O,再连接BO,并延长BO到D,使DO=BO,连接AD,CD,则四边形ABCD即为原来的平行四边形.
判定一个四边形是平行四边形可以从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理2)
一组对边平行且相等的四边形是平行四边形（判定定理1）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）