湘教版（2024）八年级下册2.5.1矩形的性质一等奖课件ppt

这是一份湘教版（2024）八年级下册2.5.1矩形的性质一等奖课件ppt，共22页。PPT课件主要包含了学习目标，新课导入，平行四边形的性质，平行四边形的对边平行，平行四边形的对边相等，平行四边形的对角相等，平行四边形的邻角互补，生活中的矩形图，知识讲解，3对角线等内容，欢迎下载使用。
1．理解矩形的概念，以及矩形与平行四边形的关系．2．探索并证明矩形的性质定理：矩形的四个角都是直角；矩形对角线相等．（重点）3.会用矩形的性质定理进行推理和计算. （重点）4.理解矩形是中心对称图形和轴对称图形.
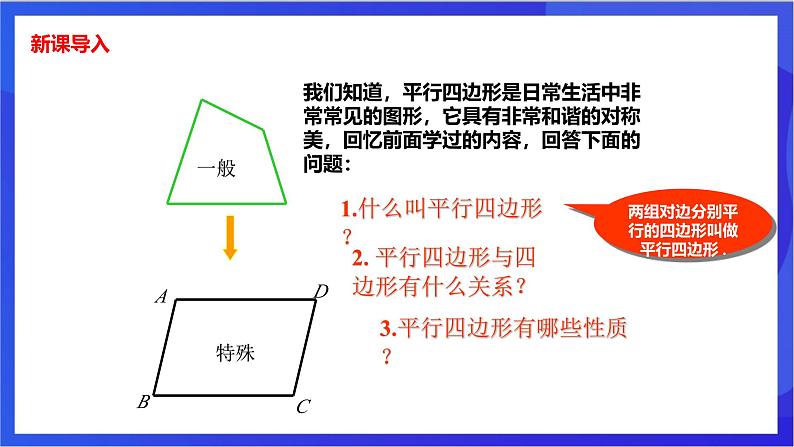
1.什么叫平行四边形？
3.平行四边形有哪些性质？
2. 平行四边形与四 边形有什么关系？
两组对边分别平行的四边形叫做平行四边形 .
我们知道，平行四边形是日常生活中非常常见的图形，它具有非常和谐的对称美，回忆前面学过的内容，回答下面的问题：
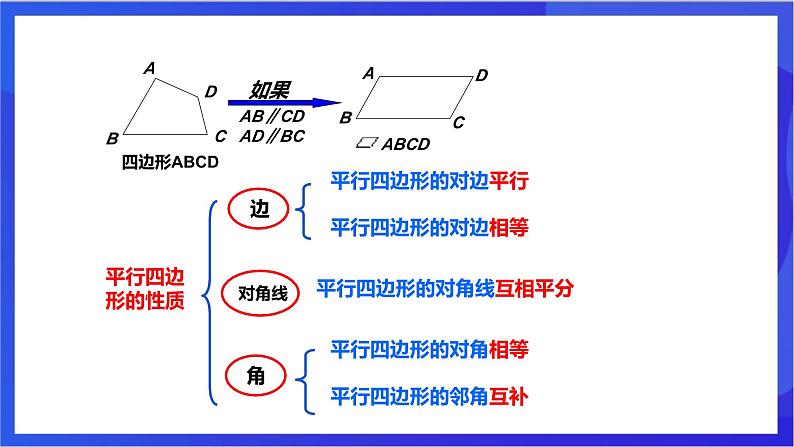
平行四边形的对角线互相平分
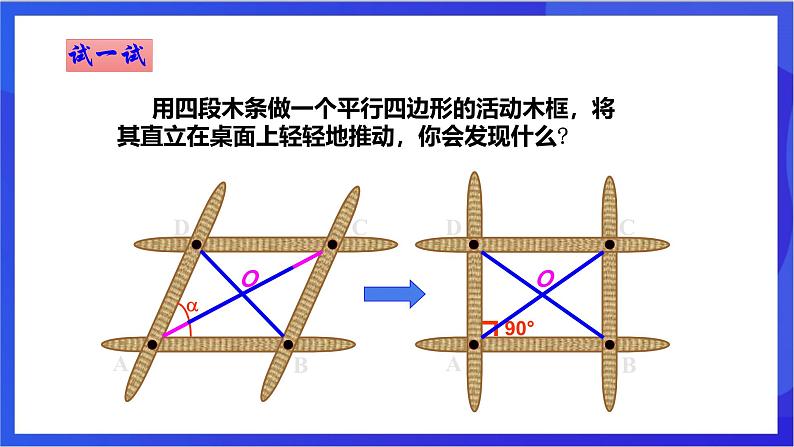
用四段木条做一个平行四边形的活动木框，将其直立在桌面上轻轻地推动，你会发现什么?
有一个角是直角的平行四边形叫作矩形，也称为长方形.
矩形是特殊的平行四边形
1.画一个矩形ABCD.
2.从边、角、对角线三方面进行考虑，你能发现矩形有什么特有的性质吗？请以小组的形式讨论总结.
四个角都是直角 　　　　
互相平分 AO＝CO; BO＝DO
平行 AD∥BC; AB∥ CD　　　 　　　　
相等 AB＝CD; AD＝BC　　　 　　　　
相 等 AC＝BD 　　 　　　　
互相垂直 AB⊥BC; AB ⊥ AD AD⊥DC;BC⊥CD
C
∠BAD＝∠ABC＝∠BCD＝∠CDA＝ 90°
矩形性质1: 矩形的四个内角都是直角，对边相等，对角线互相平分.
矩形性质2: 矩形的对角线相等．
几何语言描述：在矩形ABCD中，对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°，AC=DB， AB=CD ，AD=BC.
证明：∵AB∥DC，AD∥BC， ∴ ∠A +∠D=180° ∠A +∠B= 180°. ∠B +∠C= 180°. （两直线平行，同旁内角互补） ∵∠A = 90°， ∴ ∠A= ∠B= ∠C=∠D=90° 即矩形ABCD的四个角都是直角.
已知,平行四边形ABCD， ∠A=90°求证： ∠A=∠B=∠C=∠D=90°.
证明：∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=90°,在△ABC和△DCB中,∵AB=DC,∠ABC=∠DCB,BC= CB,∴△ABC≌△DCB.∴AC=DB.
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交于点O.求证：AC=DB.
矩形是中心对称图形，对角线的交点是它的对称中心。
矩形是轴对称图形，过每一组对边中点的直线都是矩形的对称轴，一共有2条对称轴.
矩形是中心对称图形吗？是轴对称图形吗？
即矩形ABCD的周长等于34 cm.
例2 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解：∵四边形ABCD是矩形. ∴AC = BD， OA= OC= AC,OB = OD = BD ,∴OA = OB. 又∵∠AOB=60°, ∴△OAB是等边三角形， ∴OA=AB=4， ∴AC=BD=2OA=8.
例3 如图，在矩形 ABCD中，对角线AC与BD相交于点O，AE垂直平分线段BO，垂足为点E，BD=15 cm.求AC、AB的长.
4.下列性质中，矩形不一定具有的是（ ） A.对角线相等 B.四个角都相等 C.对角线垂直 D.是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。2.有一个角是直角的四边形是矩形。（ ）3.矩形的对角线互相平分。（ ）
5.矩形具有而平行四边形不具有的性质是( ) A.两组对边分别平行 B.对角相等 C.对角线互相平分 D.对角线相等
6.矩形ABCD中，对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。A.2 B.4 C.6 D.8
7.如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于点E，AD＝8，AB＝4，求△BED的面积．
解：∵四边形ABCD是矩形，∴AD∥BC，∠A＝90°，∴∠2＝∠3.又由折叠知∠1＝∠2，∴∠1＝∠3，∴BE＝DE.设BE＝DE＝x，则AE＝8－x.∵在Rt△ABE中，AB2＋AE2＝BE2，∴42＋(8－x)2＝x2，解得x＝5，即DE＝5.∴S△BED＝ DE·AB＝ ×5×4＝10.
四个内角都是直角，对边相等两条对角线互相平分且相等
有一个角是直角的平行四边形叫作矩形
中心对称图形，对角线的交点是它的对称中心