湘教版（2024）八年级下册2.6.1菱形的性质试讲课课件ppt

这是一份湘教版（2024）八年级下册2.6.1菱形的性质试讲课课件ppt，共23页。PPT课件主要包含了学习目标，平行四边形，对角线，对边平行且相等，对角相等邻角互补，对角线互相平分，四个角是直角，对角线相等，知识回顾，新课导入等内容，欢迎下载使用。
1.理解菱形的概念及菱形与平行四边形的关系.2.探索并证明菱形的性质定理.（难点）3.能用菱形的性质进行简单的计算和推理.(重、难点）
平行四边形有哪些特征?矩形与平行四边形比较有哪些特殊的特征?
欣赏下面图片，图片中框出的图形是你熟悉的吗？
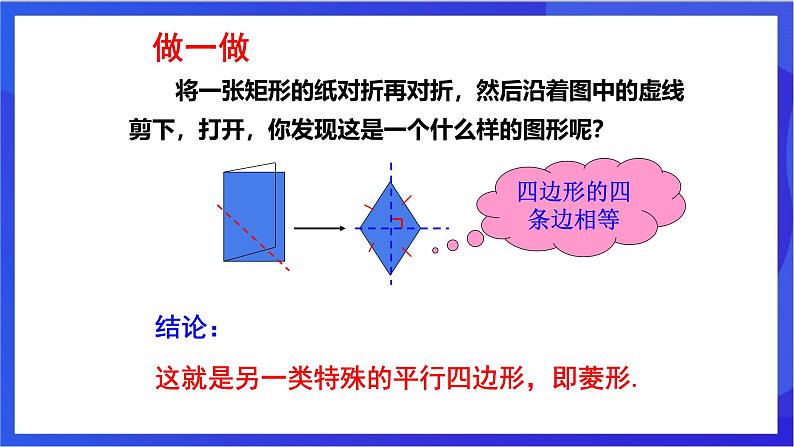
结论： 这就是另一类特殊的平行四边形，即菱形.
将一张矩形的纸对折再对折，然后沿着图中的虚线剪下，打开，你发现这是一个什么样的图形呢？
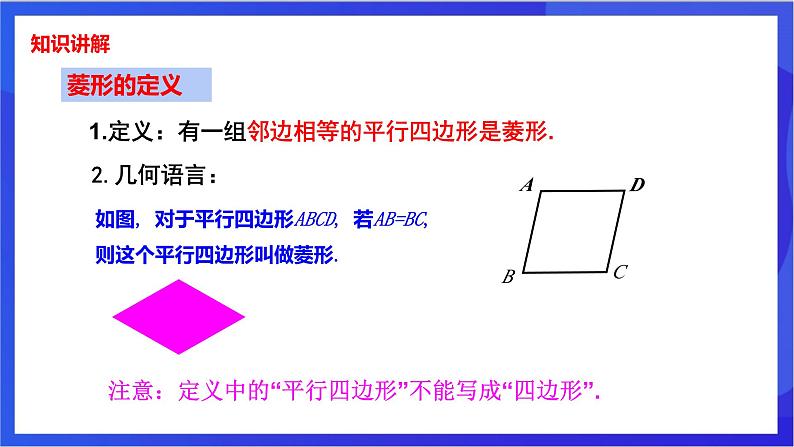
1.定义：有一组邻边相等的平行四边形是菱形.
如图, 对于平行四边形ABCD, 若AB=BC, 则这个平行四边形叫做菱形.
注意：定义中的“平行四边形”不能写成“四边形”.
菱形是特殊的平行四边形，它除具有一般平行四边形的性质外，还有哪些性质？
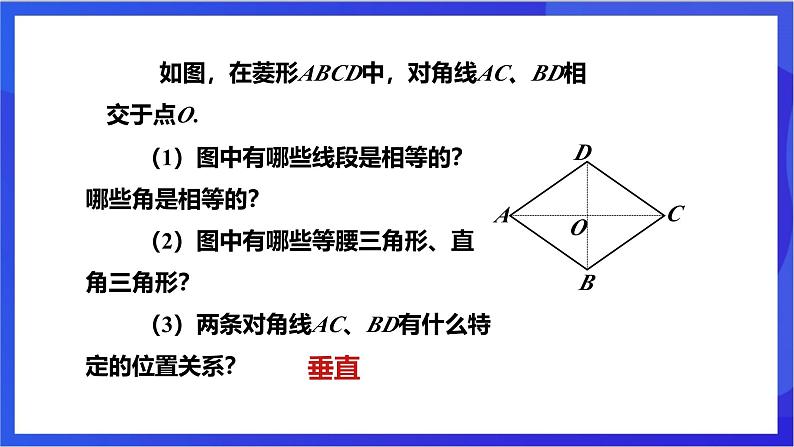
如图，在菱形ABCD中，对角线AC、BD相交于点O.
（1）图中有哪些线段是相等的？哪些角是相等的？（2）图中有哪些等腰三角形、直角三角形？（3）两条对角线AC、BD有什么特定的位置关系？
菱形除了具有平行四边形一切特征外,它还有什么特殊特征？
命题：菱形的四条边都相等
已知：如图,四边ABCD是菱形，求证：AB=BC=CD=AD.
证明：∵四边形ABCD是菱形， ∴ AB=CD，AD=BC (平行四边形的对边相等）. ∵ AB=BC， ∴ AB=BC=CD=AD.
已知：如图，菱形ABCD 的对角线AC 和BD 相交于点O.
证明：∵四边形ABCD是菱形，
∴AB=AD ，BO=DO，
∴AC⊥BD（等腰三角形的“三线合一”）.
求证：AC⊥BD.
命题：菱形的对角线互相垂直.
（1）对称性：菱形是中心对称图形，对称中心是对角线的交点；也是轴对称图形，对称轴有两条，对角线所在的直线是它的对称轴.（2）边：菱形的四条边都相等.（3）对角线：菱形的对角线互相平分且垂直.
例1 如图，在菱形ABCD中，∠BAD=2∠B，试求出∠B的度数，并说明△ABC是等边三角形.
又因为∠B+∠BAC+∠BCA=180°(三角形内角和定理)，
所以∠BAC=∠BCA=∠B=60°.
所以AB=BC=AC(等角对等边).
即△ABC是等边三角形.
例2 如图，已知菱形ABCD的边长为2cm，∠BAD＝120°，对角线AC、BD相交于点O，试求这个菱形的两条对角线AC与BD的长．
解:在菱形ABCD中，
又在△ABC中，AB＝BC，
所以∠BCA＝∠BAC＝60°(等边对等角)，
所以△ABC为等边三角形，
(菱形的每一条对角线平分一组对角)．
所以AB=BC=AC(等角对等边),
例3 如图，菱形ABCD的对角线AC、BD相交于点O,AE垂直且平分CD，垂足为点E.求∠BCD的大小.
∵四边形ABCD是菱形，
∴AD=DC=CB=BA(菱形的四条边相等).
又∵AE垂直平分CD，
∴AC=AD=DC=CB=BA，
即ΔADC和Δ ABC都为等边三角形，
∴∠ACD= ∠ACB=60°.
∴∠BCD=120°.
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗?
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢?
能. 过点A作AE⊥BC于点E,则S菱形ABCD=底×高 =BC·AE.
问题2 如图，四边形ABCD是菱形，对角线AC、BD交于点O,试用对角线表示出菱形ABCD的面积.
解：∵四边形ABCD是菱形，∴AC⊥BD,∴S菱形ABCD=S△ABC +S△ADC= AC·BO+ AC·DO= AC(BO+DO)= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半.
如图，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
解：在Rt△AOB中，OA＝5，OB＝12，∴S△AOB＝ OA·OB＝ ×5×12＝30，∴S菱形ABCD＝4S△AOB＝4×30＝120.∵且菱形两组对边的距离相等，∴S菱形ABCD＝AB·h＝13h，∴13h＝120，得h＝ .
1．若菱形的边长等于一条对角线的长，则它的一组邻角的度数分别为____和____.2．已知菱形的两条对角线分别是6cm和8cm，则菱形的周长和面积分别是______和_____．
3.如图,四边形ABCD是边长为13cm的菱形,其中对 角线BD长10cm.
求:(1)对角线AC的长度; (2)菱形ABCD的面积.
∵四边形ABCD是菱形,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
4.如图，O是菱形ABCD对角线AC与BD的交点，CD＝5cm，OD＝3cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E.(1)求OC的长；(2)求四边形OBEC的面积．
解：(1)∵四边形ABCD是菱形，∴AC⊥BD.在RT△OCD中，由勾股定理得OC＝4cm.(2)∵CE∥DB，BE∥AC，∴四边形OBEC为平行四边形.又∵AC⊥BD，即∠COB＝90°，∴平行四边形OBEC为矩形.∵OB＝OD＝3cm，∴S矩形OBEC＝OB·OC＝4×3＝12(cm2)．
1.周长=边长的四倍2.面积=底×高=两条对角线乘积的一半
1.两组对边平行且相等；2.四条边相等
两组对角分别相等，邻角互补
1.两条对角线互相垂直平分；2.每一条对角线平分一组对角