初中数学人教版（2024）九年级上册23.2.2 中心对称图形优质课ppt课件

这是一份初中数学人教版（2024）九年级上册23.2.2 中心对称图形优质课ppt课件，共17页。PPT课件主要包含了学习目标，复习引入，互动新授，中心对称图形，对角线的交点，总结归纳，小试牛刀，课堂检测，拓展训练，识别中心对称图形等内容，欢迎下载使用。
1.掌握中心对称图形的概念和性质.2.会运用中心对称图形的性质解决实际问题.3.理解中心对称与中心对称图形的区别与联系.
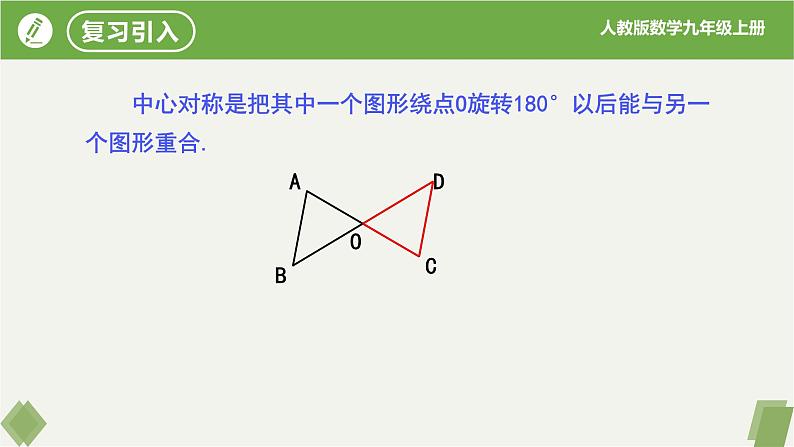
中心对称是把其中一个图形绕点O旋转180°以后能与另一个图形重合.
思考（1）如图，将线段AB绕它的中点旋转180°，你有什么发现？
可以发现：线段AB绕它的中点旋转180°后与它本身重合．
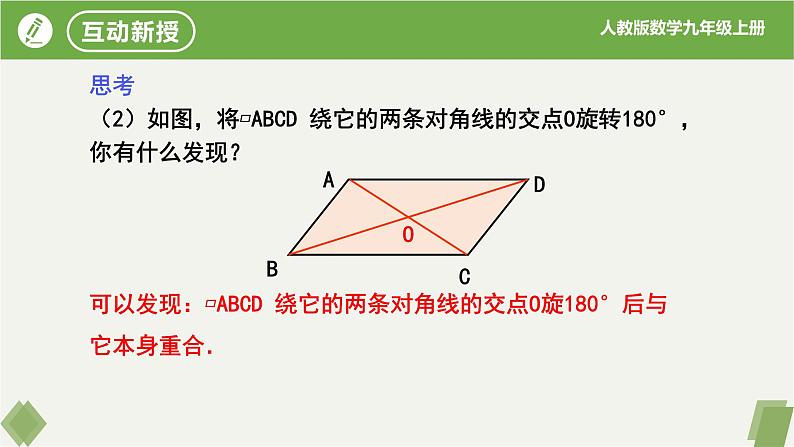
思考（2）如图，将▱ABCD 绕它的两条对角线的交点O旋转180°，你有什么发现？
可以发现：▱ABCD 绕它的两条对角线的交点O旋180°后与它本身重合．
像这样，把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心.
由上可得，线段、平行四边形都是中心对称图形.
线段、平行四边形的对称中心分别是什么？
中心对称图形的形状通常匀称美观，我们在自然界中可以看到许多美丽的中心对称图形(图(1))，在很多建筑物和工艺品中也常采用中心对称图形作装饰图案(图(2)).另外，由于具有中心对称图形形状的物体，能够在所在的平面内绕对称中心平稳地旋转，所以在各种机器中要旋转的零部件的形状常设计成中心对称图形，如水泵叶轮等(图(3)).
中心对称与中心对称图形的区别与联系 ：
(1)是针对2个图形而言的(2)是指两个图形的(位置) 关系(3)对称点在两个图形上(4)对称中心在两个图形之间
(1)是针对1个图形而言的(2)是指具有某种性质的一个图形(3)对称点在一个图形上(4)对称中心在图形上或其内部
若把成中心对称的两个图形视为一个整体，则成为中心对称图形；若把中心对称图形的两部分看作两个图形，则它们成中心对称.
1.下列图形中,既是轴对称图形,又是中心对称图形的是(　 ) A． B． C． D．2.下列图形中,既是轴对称图形又是中心对称图形的是( ) A． B． C． D．
3.下面的扑克牌中，哪些牌面是中心对称图形？
1.用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分．图 2、图 3 分别是甲、乙两同学给出的作法，对于两人的作法判断正确的是（ ） A．甲正确，乙不正确B．甲不正确，乙正确 C．甲、乙都正确 D．甲、乙都不正确
2.如图，正六边形ABCDEF的中心是点O.(1)分析它的对称性；(2)正六边形绕其中心旋转多少度可与自身重合？(3)还有哪些正多边形是中心对称图形？
解：(1)正六边形ABCDEF既是中心对称图形，又是轴对称图形．有6条对称轴．(2)旋转60°的正整数倍可与自身重合．(3)只要边数是偶数的正多边形都是中心对称图形．
1.正三角形是中心对称图形吗？正方形呢？正五边形呢？正六边呢？你能发现什么规律？
边数为偶数的正多边形都是中心对称图形.
2.（1）选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形．（2）选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．（3）选取1个涂上阴影，使4个阴影小正方形组成一个既是轴对称图形，又是中心对称图形．
判断依据：绕着内部一点旋转180度能与本身重合的图形
(1)中心对称图形上的每一对对称点所连成的线段都被对称中心平分；(2)过对称中心的直线可以把中心对称图形分成面积相等的两部分.
1.下列图形中是中心对称图形的是( )2.在下列各汽车的标志中，既是轴对称图形又是中心对称图形是( )