初中数学湘教版（2024）七年级上册（2024）3.4 一元一次方程的应用课文内容课件ppt

这是一份初中数学湘教版（2024）七年级上册（2024）3.4 一元一次方程的应用课文内容课件ppt，共20页。PPT课件主要包含了实际问题，分析问题，找出等量关系，设出未知数列出方程，检验解的合理性，解方程，20x+30x，同时出发距离相等，kmh，上午10时到等内容，欢迎下载使用。
1. 会列一元一次方程解有关追及问题、配套问题、方案设计等问题，在具体情境中建立方程模型.2. 体验建立方程模型解决问题的一般过程；体会模型转化和方程思想，增强应用意识和应用能力.3. 体会分类讨论思想和方程思想，感受数学与生活的联系，激发学生学习数学的热情.
用一元一次方程解决有关实际问题的步骤：
甲、乙两车分别从A、B两地同时出发，相向而行，甲速度为20 km/h，乙速度为30 km/h，出发 x小时后，两人相遇.
那么甲车行了______km，乙车行了______km，A、B两地相距_________km. 若A、B两站间的路程为500km，可得方程______________，求得x=____.
20x+30x=500
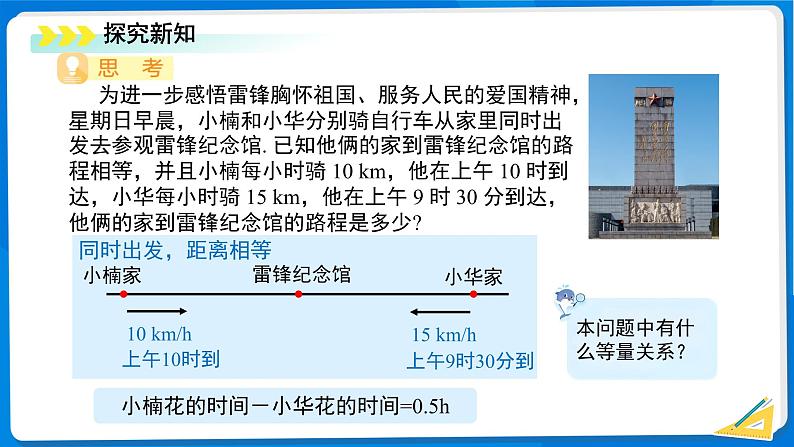
为进一步感悟雷锋胸怀祖国、服务人民的爱国精神，星期日早晨，小楠和小华分别骑自行车从家里同时出发去参观雷锋纪念馆. 已知他俩的家到雷锋纪念馆的路程相等，并且小楠每小时骑 10 km，他在上午 10 时到达，小华每小时骑 15 km，他在上午 9 时 30 分到达，他俩的家到雷锋纪念馆的路程是多少?
本问题中有什么等量关系？
小楠花的时间－小华花的时间=0.5h
例1 某校七年级甲班有45人，乙班有39人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛，已知从甲班抽调的人比乙班多1人，此时甲班剩余人数恰好是乙班剩余人数的2倍. 请问：从甲、乙两班各抽调了多少人参加歌咏比赛？
分析：本题中的等量关系： (1)甲班抽调的人数-乙班抽调的人数=1； (2)抽调后甲班剩余人数=乙班剩余人数×2 .
解：设从甲班抽调了x人，那么从乙班抽调了(x-1)人.根据题意，得 45-x=2[39-(x-1)].解得 x=35 .于是，x-1=35-1=34 .答：从甲班抽调了35人，从乙班抽调了34人参加歌咏比赛.
例2 现有树苗若干棵，计划栽在一段公路的一侧，公路的两端各栽1棵，并且相邻两棵树的间隔相等. 方案一：如果每隔5m栽1棵，则树苗缺21棵； 方案二：如果每隔5.5m栽1棵，则树苗正好用完.根据以上方案，请算出原有树苗的棵数和这段路的长度.
观察下面植树示意图，想一想：
相邻两树的间隔长、应植树棵数与路长有怎样的数量关系？
路长=相邻两树的间隔×(种植的树苗数-1)
设原有树苗x棵，由题意可得下表：
方案一和方案二的路长相等吗？
解：设原有树苗x棵，根据题意，得 5(x+21-1)=5.5(x-1) .解得 x = 211.因此，原有树苗211棵，这段公路长为 5×(211+21-1)=5×231=1155(m) .答：原有树苗211棵，这段公路长1155m.
间隔问题应用比较普遍，如路边种树，街道装路灯等． 需要注意：(1)两个端点都种上树(装上灯)，则树数－1＝间隔数；(2)两个端点都不种树(装上灯)，则树数＋1＝间隔数．
1.一队学生步行去参加社会公益活动，每小时走4km，学生甲因故推迟30 min 出发，为赶上队伍，甲以6 km/h的速度追赶，试问：甲用多长时间就可追上队伍?
解：设甲用t h就可追上队伍，根据等量关系，得4(0.5+t)=6t解得 t=1答：甲用1 h就可追上队伍.
2. 某校组织师生去参观三峡工程建设，若单独租用30 座客车若干辆，则刚好坐满；若单独租用 40 座客车，则可少租一辆，且余 20 个座位，求该校参观三峡工程建设的人数．
解：设需要 30 座的车是 x 辆，根据题意，得 30x＝40(x－1)－20，解得 x＝6.参观人数＝30×6＝180 (人)．答：该校参观三峡工程建设的人数为 180 人．
3. 某村一条道路一侧装有路灯56盏（两端都有），且相邻两盏灯的距离为30m. 为进一步建设美丽乡村，该村计划将该道路的路灯全部更换为亮度更强的节能灯，且相邻两盏灯的距离变为25m，则需要安装节能灯多少盏？
解：设需要安装节能灯x盏，根据等量关系，得 25×(x-1)=30×(56-1) 解得 x=67 答：需要安装节能灯67盏.
4.小明早晨要在 7:50 以前赶到距家 1000 米的学校上学．一天，小明以 80 米/分的速度出发，5 分钟后，小明的爸爸发现他忘了带历史作业，于是，爸爸立即以 180 米/分的速度去追小明，并且在途中追上了他．
（1）爸爸追上小明用了多长时间？ （2）追上小明时，距离学校还有多远？
分析：当爸爸追上小明时，两人所走路程相等.
解：(1) 设爸爸追上小明用了 x 分钟，则此题的数量关系可用线段图表示.
据题意，得 80×5＋80x = 180x.
答：爸爸追上小明用了 4 分钟．
（2）180×4 = 720（米），1000－720 = 280（米）.
答：追上小明时，距离学校还有 280 米．
解得 x = 4.
① 要善于分析问题中的不变量，并利用不变量来列方程；② 要善于用不同的方式表示同一个量，由此得到相等关系，从而列出方程．
1. 追及问题：追者路程＝被追者路程＋相隔距离