高中通用技术模型综合训练题

这是一份高中通用技术模型综合训练题，共10页。试卷主要包含了“母子”模型，CD2＝AC•BD．等内容，欢迎下载使用。
母子相似证明题一般思路方法:
①由线段乘积相等转化成线段比例式相等；
②分子和分子组成一个三角形、分母和分母组成一个三角形；
③第②步成立，直接从证这两个三角形相似，逆向证明到线段乘积相等；
④第②步不成立，则选择替换掉线段比例式中的个别线段，之后再重复第③步。
模型1.“母子”模型(共边角模型)
【模型解读与图示】“母子”模型的图形（通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀），也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．

图1 图2 图3 图4
1）“母子”模型（斜射影模型）
条件：如图1，∠C=∠ABD； 结论：△ABD∽△ACB，AB2＝AD·AC.
2）双垂直模型（射影模型）
条件:如图2，∠ACB=90，CD⊥AB；
结论：△ACD∽△ABC∽△CBD；CA2＝AD·AB，BC2＝BD·BA，CD2＝DA·DB.
3）“母子”模型（变形）
条件:如图3，∠D=∠CAE，AB=AC； 结论：△ABD∽△ECA；
4）共边模型
条件:如图1，在四边形中，对角线平分，，结论：；
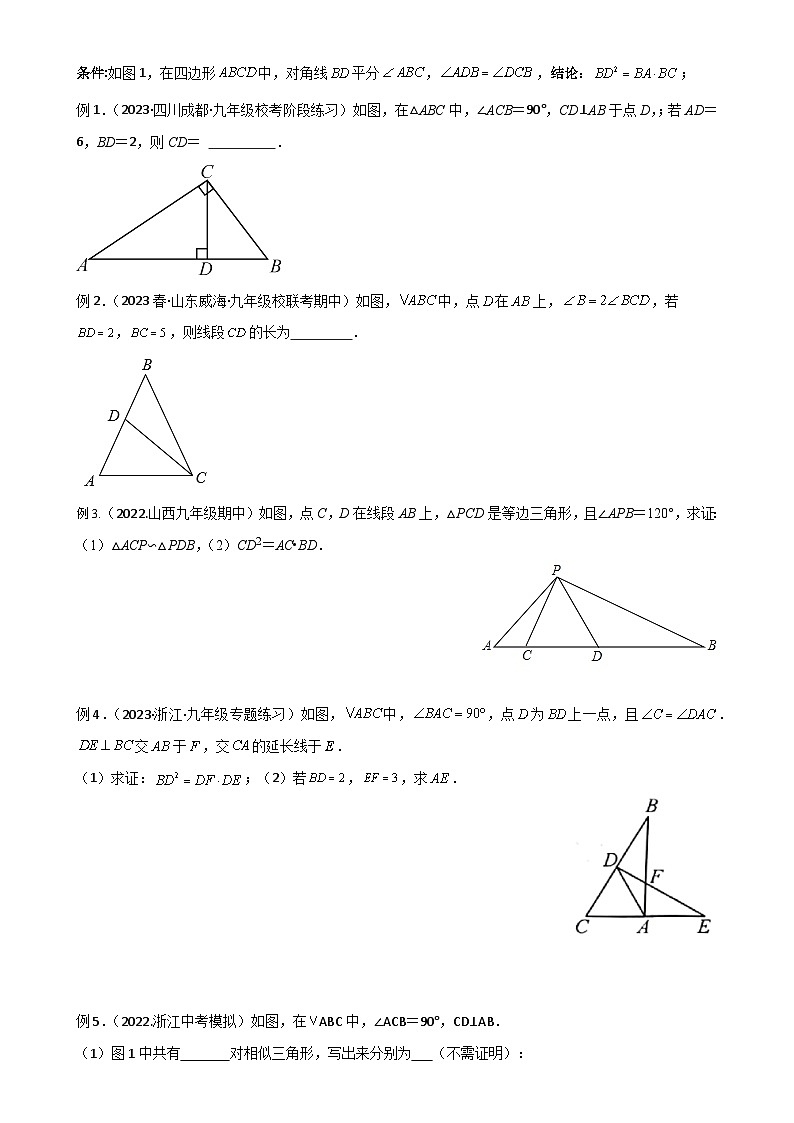
例1．（2023·四川成都·九年级校考阶段练习）如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，；若AD＝6，BD＝2，则CD＝ ．
例2．（2023春·山东威海·九年级校联考期中）如图，中，点在上，，若，，则线段的长为 ．
例3.（2022.山西九年级期中）如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．
例4．（2023·浙江·九年级专题练习）如图，中，，点为上一点，且．交于，交的延长线于．
（1）求证：；（2）若，，求．
例5．（2022.浙江中考模拟）如图，在ABC中，∠ACB＝90°，CD⊥AB．
（1）图1中共有 对相似三角形，写出来分别为 （不需证明）：
（2）已知AB＝5，AC＝4，请你求出CD的长：
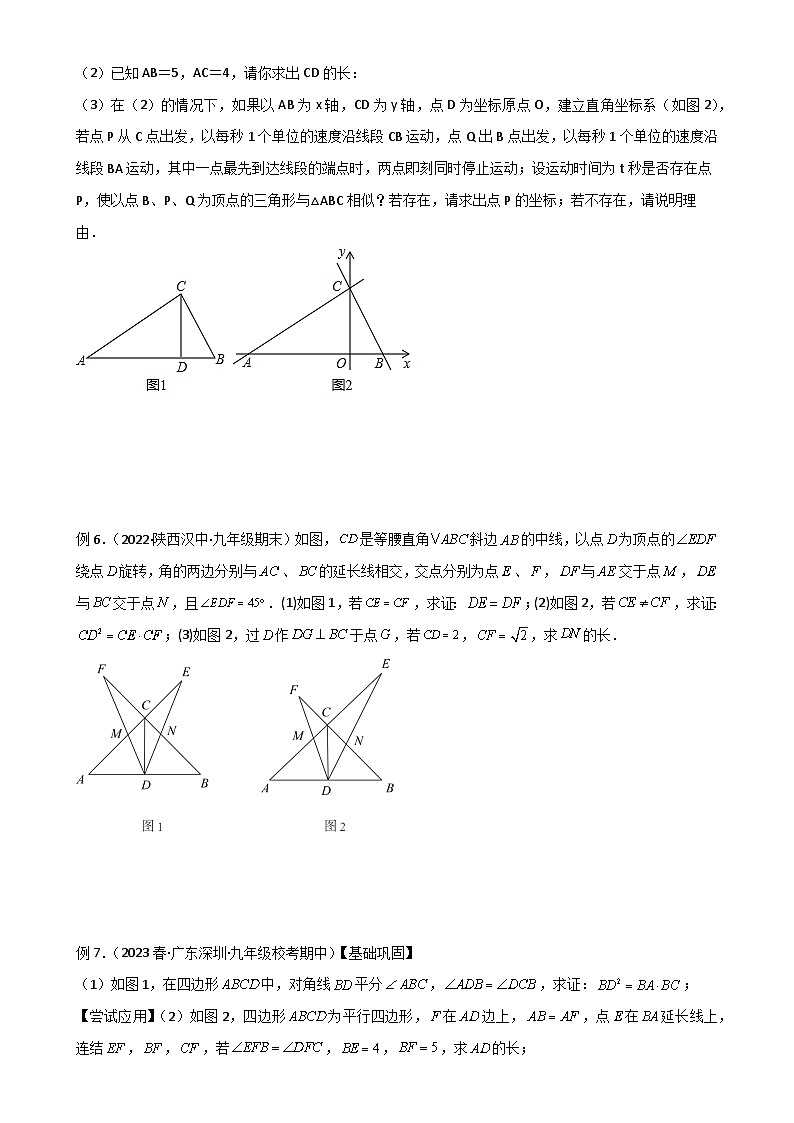
（3）在（2）的情况下，如果以AB为x轴，CD为y轴，点D为坐标原点O，建立直角坐标系（如图2），若点P从C点出发，以每秒1个单位的速度沿线段CB运动，点Q出B点出发，以每秒1个单位的速度沿线段BA运动，其中一点最先到达线段的端点时，两点即刻同时停止运动；设运动时间为t秒是否存在点P，使以点B、P、Q为顶点的三角形与△ABC相似？若存在，请求出点P的坐标；若不存在，请说明理由．
例6．（2022·陕西汉中·九年级期末）如图，是等腰直角斜边的中线，以点为顶点的绕点旋转，角的两边分别与、的延长线相交，交点分别为点、，与交于点，与交于点，且．(1)如图1，若，求证：；(2)如图2，若，求证：；(3)如图2，过作于点，若，，求的长．
例7．（2023春·广东深圳·九年级校考期中）【基础巩固】
（1）如图1，在四边形中，对角线平分，，求证：；
【尝试应用】（2）如图2，四边形为平行四边形，在边上，，点在延长线上，连结，，，若，，，求的长；
【拓展提高】（3）如图3，在中，是上一点，连结，点，分别在，上，连结，，，若，，，，，求的值．

课后专项训练
1．（2023秋·北京延庆·九年级统考期中）如图，点是的边上一点，要使得与相似，添加一个条件，不正确的是（ ）
A． B． C． D．
2．（2022秋·河北保定·九年级统考期中）如图，已知，其中，，则（ ）
A．2B．C．D．4
3．（2023春·浙江台州·九年级校考阶段练习）如图，在中，，过点C作于点D，点M为线段的中点，连接，过点D作于点E．设，，则图中可以表示为的线段是（ ）

A． B． C． D．
4．（2023秋·浙江金华·九年级校考阶段练习）如图，D是的边上一点，连接，若，则的长 ．

5．（2023秋·浙江宁波·九年级校联考阶段练习）已知：如图，中，，，D为边上一点，． (1)求证： ．(2)若的周长为11，请求出的长．

6．（2022·湖北武汉·校考模拟预测）已知，点D在的边上，连接． (1)如图1，若．求证：；(2)如图2，若，，，．求线段的长；(3)如图3，M、N分别是上的两点，连接交于点P，当，时，若，直接写出的值______．

7．（2023秋·上海闵行·九年级统考期中）如图，在梯形中，，，点E是边中点，连接并延长交的延长线于点F，，且．
(1)求证：；(2)求证：．

8．（2023秋·安徽亳州·九年级统考阶段练习）如图，在的边长为1的小正方形网格中，的三个顶点都在格点上．

(1)直接写出的形状______；(2)若垂足为D，证明：；
(3)拓展应用：在A时测得某树（垂直于地面）的影长为4米，C时又测得该树的影长为16米，若两次日照的光线互相垂直，则树的高度为______米．（直接写出结果）
9．（2022春·广东惠州·九年级校考开学考试）如图，是的直径，点D是上一点，且，与交于点F．(1)求证：是的切线；(2)若平分，求证：．
10．（2022·湖南长沙·校考三模）约定：若三角形一边上的中线将三角形分得的两个小三角形中有一个三角形与原三角形相似，我们则称原三角形为关于该边的“华益美三角”．例如，如图1，在中，为边上的中线，与相似，那么称为关于边的“华益美三角”．

(1)如图2，在中，，求证：为关于边的“华益美三角”；
(2)如图3，已知为关于边的“华益美三角”，点是边的中点，以为直径的⊙恰好经过点．①求证：直线与相切；②若的直径为，求线段的长；
(3)已知为关于边的“华益美三角”，，，求的面积．
11．（2023秋·河北邢台·九年级统考阶段练习）如图，在中，是边上一点．
(1)当时，①求证：；②若，，求的长；
(2)已知，若，求的长．

12．（2022·广东茂名·统考二模）如图所示，点在同一直线上，满足，，且．求证：．
13．（2022·湖北武汉·校考模拟预测）如图1，中，，D为上一点，．

(1)求证：；(2)如图2，过点A作于M，交于点E，若，求的值；
(3)如图3，N为延长线上一点，连接、，若，，则 的值为_．
14．（2023·吉林·九年级阶段练习）【基础巩固】（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．
【尝试应用】（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF＝4，BE＝3，求AD的长．
15．（2023·福建九年级期中）如图，在△ABC中，D是BC上的点，E是AD上一点，且，∠BAD＝∠ECA．（1）求证：AC2＝BC•CD；（2）若AD是△ABC的中线，求的值．
16．（2022秋·广东九年级课时练习）如图，点C、D在线段AB上，且△PCD是等边三角形．∠APB＝120°．
（1）求证：△ACP∽△PDB；（2）当AC＝4，BD＝9时，试求CD的值．
17．（2023秋·江苏扬州·九年级校联考阶段练习）如图，，平分，连接交于.(1)求证：；(2)若，，求的长.
18．（2022春·湖北武汉·九年级校考阶段练习）（1）[问题背景]如图1，在四边形中，对角线平分，且满足，求证：
（2）[尝试应用]在中，的角平分线交于点F
①如图2，，边上一点G满足，，，求的值．
[拓展创新]②如图3，，，，，直接写出的值（用含有m、n、a三个字母的代数式表示）为__________．