初中数学北师大版（2024）八年级上册3 勾股定理的应用图文ppt课件

这是一份初中数学北师大版（2024）八年级上册3 勾股定理的应用图文ppt课件，共39页。PPT课件主要包含了赵爽弦图，刘徽“青朱出入图”，加菲尔德总统拼图，毕达哥拉斯拼图，知识回顾，学习目标，课堂导入，跟踪训练，新知探究，随堂练习等内容，欢迎下载使用。
勾股定理的4种证明方法：
1.熟练运用勾股定理及其逆定理解决实际问题.2.进一步加深对勾股定理与其逆定理之间关系的认识.3.学会将实际问题构建成数学模型，并运用勾股定理的逆定理解决.
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面，3尺高处出红莲.亭亭多姿湖中立，突遭狂风吹一边.离开原处6尺远，花贴湖面像睡莲.请君动脑想一想，湖水在此深几尺？
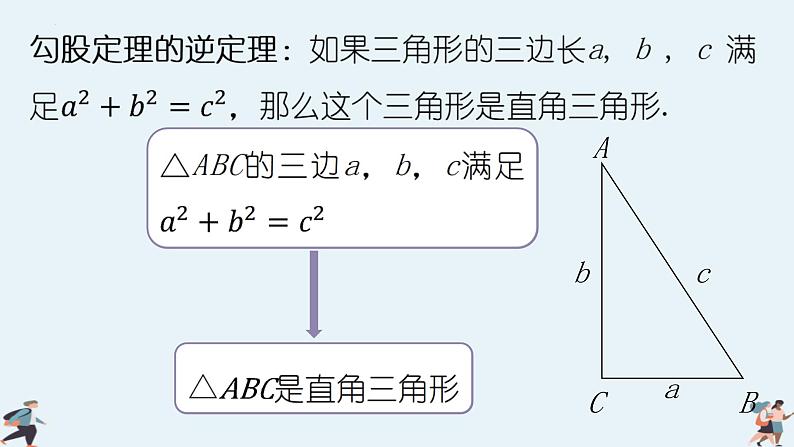
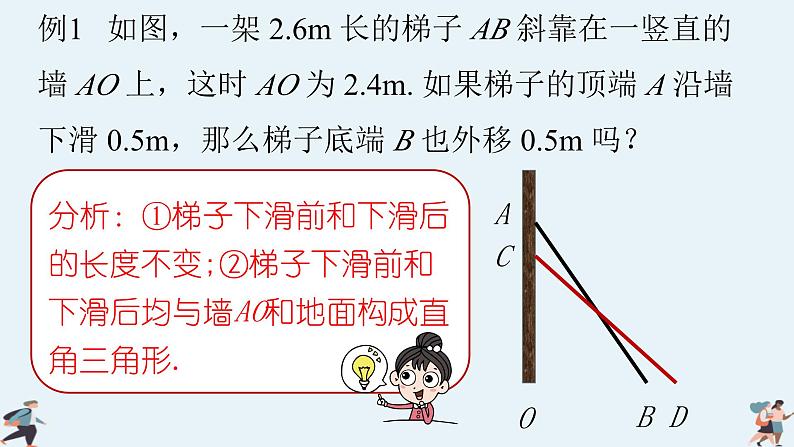
分析：①梯子下滑前和下滑后的长度不变;②梯子下滑前和下滑后均与墙AO和地面构成直角三角形.
例1 如图，一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上，这时 AO 为 2.4m. 如果梯子的顶端 A 沿墙下滑 0.5m，那么梯子底端 B 也外移 0.5m 吗？
所以梯子的顶端下滑0.5m时，梯子底端并不是也外移0.5m，而是外移约0.77m.
运用勾股定理解决实际问题的一般步骤1.从实际问题中抽象出几何图形；2.确定所求线段所在的直角三角形；3.找准直角边和斜边，根据勾股定理建立等量关系；4.求得结果.
勾股定理应用的常见类型1.已知直角三角形的任意两边求第三边；2.已知直角三角形的任意一边确定另两边的关系；3.证明包含有平方（算术平方根）关系的几何问题；4.求解几何体表面上的最短路程问题；5.构造方程（或方程组）计算有关线段长度，解决生产、生活中的实际问题.
1.在一次台风中，小红家的树在离地面 3 米的地方被拦腰截断，树的顶部落在离根部 4 米的地方，你能计算出这棵树没截断前的高度吗？
分析：根据题意，可以将地面、截断倒地的树的部分、剩余未截断的树的部分构建成一个直角三角形.
分析：根据勾股定理可以得出直角三角形的第三边也相等，然后利用“三边相等”来证明全等.
1.如图，池塘边有两点 A，B，点 C 是与 BA 方向成直角的AC 方向上一点，测得 BC=60m，AC=20m. 求 A，B 两点间的距离（结果取整数）.
2.《九章算术》中一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AC生长在它的中央，高出水面部分BC为1尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部C恰好碰到岸边的C'处（如图1），水深和芦苇长各多少尺？则该问题的水深是 ______尺．
解：把台阶展成如图的平面图形，连接AB.
3.如图，台阶下 A 处的蚂蚁要爬到 B 处搬运食物，它走的最短路程是多少？
1.小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为 0.7 米，顶端距离地面 2.4 米.如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面 2米，则小巷的宽度为（ C ）.
A. 0.7米 B. 1.5米C. 2.2米 D. 2.4米
2.已知一个三角形工件尺寸如图，计算高 l 的长（结果取整数）.
解：如图，过点A作AD⊥BC于点D.
3.有一块土地形状如图所示， ∠B=∠D=90〫，AB=20米，BC=15米， CD=7米，请计算这块土地的面积.
解：连接AC，则S四边形ABCD= S△ABC + S△ADC.
答：这块土地的面积为234平方米.
思考 我们已经学会用勾股定理解决实际问题，那么勾股定理的逆定理在实际生活中有哪些应用呢？
船只在航行的时候需要确定方向和位置.
如图，某港口 P 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行， “远航”号每小时航行 16n mile，“海天”号每小时航行 12n mile.它们离开港口一个半小时后分别位于点 Q，R 处，且相距 30n mile.如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
知识点1：勾股定理逆定理的应用
通过题目已知条件可以得出：1.PR 的长度 2. PQ 的长度3.∠1 的度数 4. RQ 的长度
分析：在图中可以看到，由于“远航”号的航向已知，如果求出两艘轮船的航向所成的角，就能知道 “海天”号的航向了.
解：根据题意，PQ=16×1.5=24， PR=12×1.5=18， RQ=30.
所以∠RPQ=90〫.
由“远航”号沿东北方向航行可知， ∠1=45〫 .因此∠2=45〫，即“海天”号沿西北方向航行.
1. A，B，C 三地的两两距离如图所示，A 地在 B 地的正东方向，C 地在 B 地的什么方向？
分析：根据图示的距离，可以判断出以 A，B，C 三地位置构成的三角形是直角三角形.
解：设A，B，C三地对应点A，B，C，则在△ABC中，
所以△ABC是直角三角形，且∠B=90〫，所以 C 地在 B 地的正北方向 .
2.如图，在四边形ABCD中，AB=3，BC=4，CD=12，AD=13， ∠B=90〫.求四边形ABCD的面积.
分析：△ABC是直角三角形，所以可以求出斜边 AC. 根据 AC，CD，AD 的长度及勾股定理的逆定理可以判定△ACD也是直角三角形.
所以△ACD是直角三角形，且∠ACD=90〫.
3.小明向东走 80m 后，沿另一方向又走了 60m，再沿第三个方向走 100m 回到原地.小明向东走 80m 后是向哪个方向走的？
分析：如图所示，小明先向东走到 A 处，则 OA=80m. 根据题意，小明应该是往东西方向坐标以上或者以下行走的，所以应该分两种情况讨论.
解：（1）小明从O走到A，再走到B1，最终由B1回到O.
所以△AOB1是直角三角形，且∠OAB1 =90〫.因此小明向东走 80m 后，又向北走了 60m，再走 100m 回到原地.
（2）小明从O走到A，再走到B2，最终由B2回到O.
同理，△AOB2是直角三角形，且∠OAB2 =90〫.因此小明向东走 80m 后，又向南走了 60m，再走 100m 回到原地.
综上所述，小明向东走 80m 后，又向南或向北走了 60m，最后走 100m 回到原地.
1.如图所示，甲、乙两船从港口 A 同时出发，甲船以 30 海里/时的速度向北偏东 35〫的方向航行，乙船以 40 海里/时的速度向另一方向航行，2 小时后，甲船到达 C 岛，乙船到达 B 岛，若 C，B 两岛相距 100 海里，则乙船航行的方向是南偏东多少度？
解：由题意得：AC=30×2=60（海里）， AB=40×2=80（海里）.
2.某探险队的 A 组从驻地 O 点出发，以 12km/h 的速度前进，同时 B 组也从驻地 O 点出发，以 9km/h 的速度向另一方向前进. 2h 后同时停下来，如图所示，这时 A，B 两组相距 30km. 此时，A，B 两组行进的方向成直角吗？请说明理由.
解：因为出发2小时，A组行了12×2=24（ km ），B组行了9×2=18（km）.
所以A，B两组行进的方向成直角.