冀教版（2024）七年级上册（2024）第五章 一元一次方程5.4 一元一次方程的应用教案配套课件ppt

这是一份冀教版（2024）七年级上册（2024）第五章 一元一次方程5.4 一元一次方程的应用教案配套课件ppt，共20页。PPT课件主要包含了图片替换区，路程＝速度×时间，小明跑步的路程，15-x，xkm，相遇地点，轿车行驶的路程，公共汽车行驶的路程，工程问题解题思路等内容，欢迎下载使用。
1.掌握相遇问题、工程问题中的基本等量关系；2.学会利用线段图分析相遇问题及工程问题，找出等量关系，准确列出方程；3.进一步体会方程这一数学模型的重要作用，增强数学的应用意识，发展模型观念.
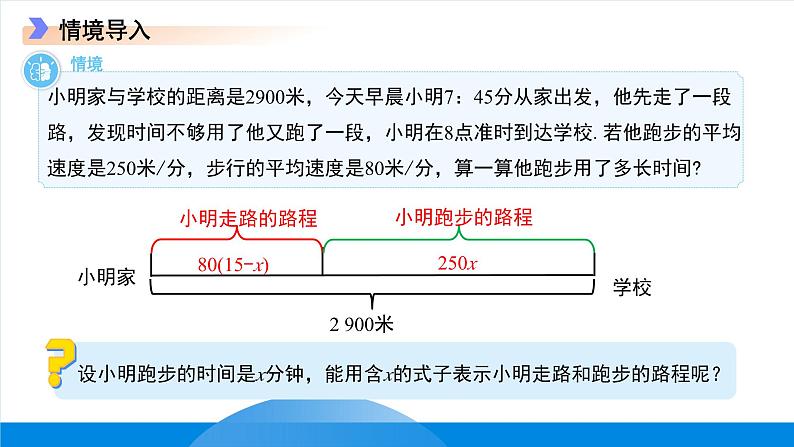
小明家与学校的距离是2900米，今天早晨小明7：45分从家出发，他先走了一段路，发现时间不够用了他又跑了一段，小明在8点准时到达学校.若他跑步的平均速度是250米/分，步行的平均速度是80米/分，算一算他跑步用了多长时间?
解：设小明跑步的时间是x分钟，根据题意，得80(15-x) +250x=2900. 解这个方程，得x=10.答：小明跑步的时间是10分钟．
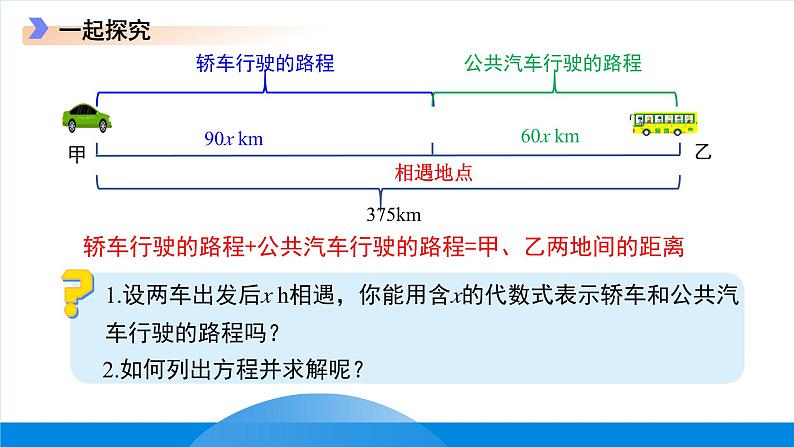
甲、乙两地间的路程为375km．一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行．轿车的平均速度为90km/h，公共汽车的平均速度为60km/h.它们出发后多长时间相遇？
1.设两车出发后x h相遇，你能用含x的代数式表示轿车和公共汽车行驶的路程吗？
轿车行驶的路程+公共汽车行驶的路程=甲、乙两地间的距离
2.如何列出方程并求解呢？
解：设两车出发后xh相遇， 根据题意，得90x+60x=375. 解这个方程，得x=2.5.答：它们出发后2.5小时相遇．
相遇问题中常见的等量关系:
注意：相向而行的始发时间和相遇地点.
一项工作，小李单独做需要6h完成，小王单独做需要9h完成.如果小李先做2h后，再由两人合做，那么还需几小时才能完成？
小李单独做2h的工作量十小王、小李合做完成的工作量=工作总量
1.三个基本量：工程问题中的三个基本量：工作总量、工作效率、工作时间，它们之间的关系：工作总量=工作效率×工作时间.若把工作总量看作1，则工作效率=1÷工作时间.
2.相等关系：(1)按工作时间：各时间段的工作量之和=完成的工作总量.(2)按工作者： 若一项工作由甲、乙两人参与，则甲的工作量+乙的工作量=完成的工作总量.
1.甲、乙两人骑自行车，同时从相距14km的两地相向而行，甲的速度为12km/h，乙的速度为16km/h，他们出发后多长时间相遇？
解：设他们出发后 xh相遇，依据题意，得 12x+16x=14.　　解这个方程，得x=0.5.答：他们出发后0.5h相遇．
2.为使福利院的孩子们度过一个快乐的儿童节，某玩具工厂决定赠送他们一批玩具，这批玩具甲组独立生产需要10天完成，乙组独立生产需要6天完成.甲组独立生产2天后，乙组开始参与生产，两组合做多少天可以完成这批玩具的生产任务?
答：两组合做3天可以完成这批玩具的生产任务.
1.甲、乙两人骑摩托车同时从相距170千米的A，B两地相向而行，2小时相遇，如果甲比乙每小时多行5千米，则乙每小时行(　　) A．30千米 B．40千米 C．50千米 D．45千米
2.甲、乙两人在400米的环形跑道上练习长跑，他们同时同地反向而跑，甲的速度是6米/秒，乙的速度是4米/秒，则他们首次相遇时，两人都跑了(　　) A．40秒 B．50秒 C．60秒 D．70秒
3.一项工程，甲单独做需要9天完成，乙单独做需要12天完成.甲、乙两人合作3天后，甲有其他任务，剩下的工程由乙单独完成.那么乙还需要几天才能完成全部工程？
答：乙还需要5天才能完成全部工程.
1.如何应用一元一次方程解决相遇问题？2.如何应用一元一次方程解决工程问题？