






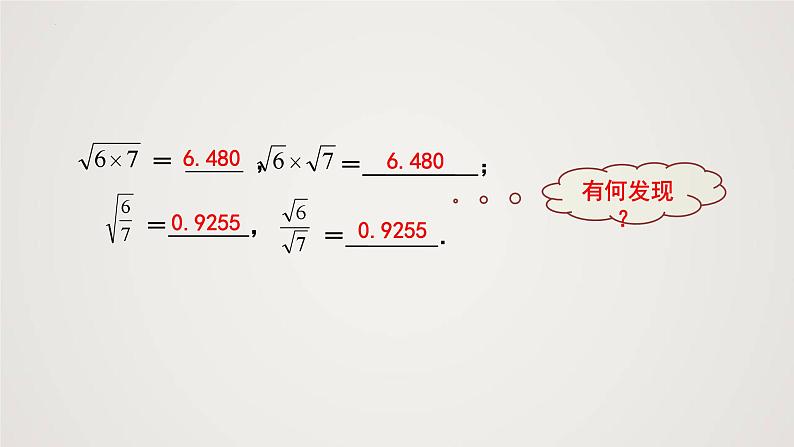
所属成套资源:2024年北师大版数学八上同步精品课件
初中数学北师大版(2024)八年级上册7 二次根式授课课件ppt
展开
这是一份初中数学北师大版(2024)八年级上册7 二次根式授课课件ppt,共20页。PPT课件主要包含了学习目标,情境导入,探索交流,例题解析,有何发现,a≥0b≥0,a≥0b>0,例2化简,最简二次根式,例3化简等内容,欢迎下载使用。
1.了解二次根式的定义及最简二次根式;(重点)2.运用二次根式有意义的条件解决相关问题.(难点)
问题1 什么叫做平方根?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
问题2 什么叫做算术平方根?
如果 x2 = a(x≥0),那么 x 称为 a 的算术平方根.用 表示.
问题3 什么数有算术平方根?
我们知道,负数没有平方根.因此,在实数范围内开平方时,被开方数只能是正数或0.
观察下列代数式:可以发现,这些式子我们在前面都已学习过,它们的共同特征是:(1)都含有开平方运算;(2)并且被开方数都是非负数.
注意:a可以是数,也可以是代数式.
例1.下列各式中,哪些是二次根式?哪些不是?
解:(1)(4)(6)均是二次根式,其中a2+1属于“非负数+正数”的形式一定大于零.(3)(5)(7)均不是二次根式.
(1)计算下列各式,你能得到什么猜想?(2)根据上面的猜想,估计下面每组两个式子是否相等,借助计算器验证,并与同伴进行交流.
a、b必须都是非负数!
积的算术平方根等于它们算术平方根的积
a必须是非负数,b必须是正数!
商的算术平方根等于它们算术平方根的商
注意:公式中的a,b 既可以是一个数,也可以是一个式子.积中各个因式必须都为非负数,若不是非负数,应将其化成非负数再运用公式化简.
结果应化为最简二次根式
1.满足下列条件的二次根式,叫做最简二次根式(1)被开方数中不含分母;(2)被开方数中不含能开得尽方的因数或因式;(3)分母中不含根号。
注意:化简时,通常要求最终结果中分母不含有根号,而且各个二次根式是最简二次根式.
2.二次根式化简成最简二次根式的步骤:(1)“一分”,即利用因数(式)分解的方法把被开方数的分子、分母都化成质因数(式)的幂的乘积形式; (2)“二移”, 即把能开得尽方的因数(式)用它的算术平方根代替,移到根号外,其中把根号内的分母中的因式移到根号外时,要注意应写在分母的位置上;(3)“三化”,即化去被开方数中的分母.
将被开方数分解成平方因数与其他因数相乘的形式!
分母含有根号,将分母进行有理化
1.下列二次根式中,是最简二次根式的是 ( ).
2.式子 有意义的条件是 ( )
A.x>2 B.x≥2 C.x<2 D.x≤2
3.若 是整数,则自然数n的值有 ( ) A.7个 B.8个 C.9个 D.10个
4.计算下列各式的值。
相关课件
这是一份初中数学北师大版(2024)八年级上册7 二次根式示范课课件ppt,共19页。PPT课件主要包含了学习目标,情境导入,什么叫二次根式,两个基本性质,探索交流,还记得吗,新的用法,例题解析,例1计算下列的式子,例2计算等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)八年级上册7 二次根式课前预习课件ppt,共60页。PPT课件主要包含了知识回顾,二次根号,被开方数,读作根号a,新知探究,跟踪训练,被开方数为非负数,分母不能为0,2原式5,-aa0等内容,欢迎下载使用。
这是一份北师大版(2024)八年级上册7 二次根式课文内容ppt课件,共21页。PPT课件主要包含了学习目标,导入新课,讲授新课,①根指数都为2,②被开方数为非负数,要点归纳,是否含二次根号,被开方数是不是非负数,二次根式,不是二次根式等内容,欢迎下载使用。










