数学北师大版（2024）第七章 平行线的证明5 三角形的内角和定理课堂教学课件ppt

这是一份数学北师大版（2024）第七章 平行线的证明5 三角形的内角和定理课堂教学课件ppt，共23页。PPT课件主要包含了学习目标，情境导入，探索交流，已知△ABC，思路总结，作辅助线，例题解析，基本图形，练习巩固等内容，欢迎下载使用。
2.会运用三角形内角和定理进行计算.（难点）
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.（重点）
我的形状最小，那我的内角和最小.
我的形状最大，那我的内角和最大.
不对，我有一个钝角，所以我的内角和才是最大的.
一天，三类三角形通过对自身的特点，讲出了自己对三角形内角和的理解，请同学们作为小判官给它们评判一下吧.
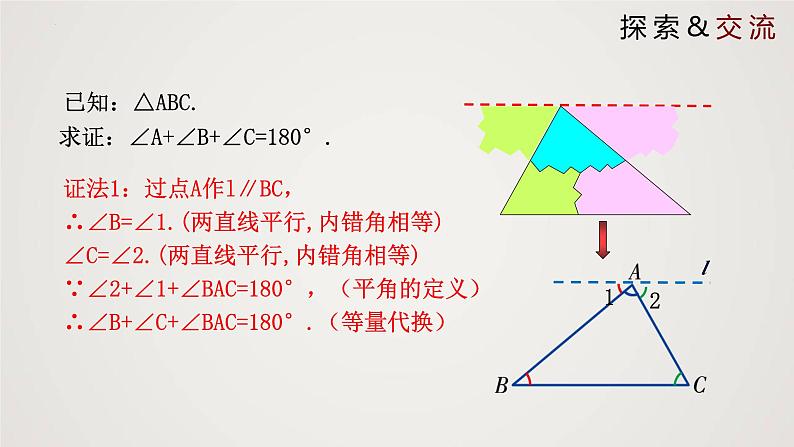
我们知道，三角形内角和等于180°.你还记得这个结论的探索过程吗？（1）如图，如果我们只把∠A移到∠1的位置，你能说明这个结论吗？如果不移动∠A，那么你还有什么方法可以达到同样的效果？（2）根据前面给出的基本事实和定理，你能用自己的语言说说这一结论的言写出这一证明过程吗？与同伴进 行交流.
求证：∠A+∠B+∠C=180°.
证法1：过点A作l∥BC，∴∠B=∠1.(两直线平行,内错角相等) ∠C=∠2.(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°，（平角的定义）∴∠B+∠C+∠BAC=180°.（等量代换）
证法2：延长BC到D，过点C作CE∥BA，∴∠A=∠1 .(两直线平行，内错角相等)∠B=∠2.(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180°，（平角的定义）∴∠A+∠B+∠ACB=180°.（等量代换）
1.三角形内角和定理：三角形的内角和等于180°.2.三角形内角和定理的证明思路：思路一：利用“两直线平行，内错角及同位角相等”将三角形的三个内角转化为一个平角. 如图3 ①② . 思路二：利用“两直线平行，内错角相等”将三角形的三个内角转化为两平行线间的一组同旁内角. 如图4 ①② .
在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线.在平面几何里，辅助线通常画成虚线.
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等，这种转化思想是数学中的常用方法.
例1.∠A，∠B，∠C 是△ABC 的三个内角. （1）已知∠A=40°，∠B= ∠C，求∠B，∠C 的度数； （2）已知∠A-∠B=16°，∠C=54°，求∠A，∠B 的度数； （3）已知∠A= ∠B= ∠C，求∠A，∠B，∠C 的度数.
解：（1）设∠ B= ∠ C=x°， ∵∠ A+ ∠ B+ ∠ C=180°，∴ 40+x+x=180， 解得x=70，∴∠ B= ∠ C=70° . （2） 设∠ A=x°，∠ B=y°， ∵∠ A+ ∠ B+ ∠ C=180°， ∴ ∴∠ A=71°，∠ B=55°.
（3） ∵∠A = ∠B = ∠C， ∴∠B=2∠A，∠C=3∠A. 设∠ A=x°，则∠ B=2x°，∠ C=3x°，∵∠A+ ∠B+ ∠C=180°， ∴ x+2x+3x=180. ∴ x=30. ∴∠A=30°，∠B=60°，∠C=90°
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗?请你帮小明把想法化为实际行动.证明:过点A作PQ∥BC,则 ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3=180° (平角的定义), ∴∠BAC+∠B+∠C=180° (等量代换).小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?
已知：直角三角形ABC中， ∠C＝90°求证： ∠A 与∠B互余.证明：∵∠A＋∠B＋∠C＝180°（三角形内角和定理） ∠C＝90°（已知）∴∠A＋∠B＝90°.(等量减等量差相等)∴∠A与∠B互余.（两角互为余角的定义）
例2.如图，在△ABC中，AD是高，AE是∠BAC的平分线，∠B＝20°，∠C＝60°.求∠DAE的度数．
解：在△ABC中，∠B＝20°，∠C＝60°，所以∠BAC＝180°－∠B－∠C＝100°.又因为AE是∠BAC的平分线，所以∠BAE＝在△ABD中，∠B＋∠BAD＋∠BDA＝180°.又因为AD是高，所以∠BAD＝180°－20°－90°＝70°.所以∠DAE＝∠BAD－∠BAE＝70°－50°＝20°.
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
例3.在△ABC 中， ∠A 的度数是∠B 的度数的3倍，∠C 比∠B 大15°，求∠A，∠B，∠C的度数.
解: 设∠B为x°，则∠A为(3x)°，∠C为(x ＋ 15)°， 从而有
3x ＋ x ＋(x ＋ 15)＝ 180.
解得 x ＝ 33.
所以 3x ＝ 99 ， x＋15＝ 48.
答：∠A，∠B，∠C的度数分别为99°，33°，48°.
几何问题借助方程来解. 这是一个重要的数学思想.
例4.如图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西40°方向.从B岛看A,C两岛的视角∠ABC是多少度？从C岛看A、B两岛的视角∠ACB是多少度？
解：∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °-∠BAD=180°-80°=100°,∠ABC=∠ABE-∠EBC=100°-40°=60°.
在△ABC中，∠ACB=180 °-∠ABC-∠CAB=180°-60°-30° =90°,
答：从B岛看A,C两岛的视角∠ABC是60°,从C岛看A,B两岛的视角∠ACB是90°.
1.在△ABC中，∠A∶∠B∶∠C＝3∶4∶5，则∠C等于(　　)A．45° B．60° C．75° D．90°
2.如图所示，在△ABC中，CD是∠ACB的平分线，∠A=80°，∠B=60°，那么∠BDC=( )A.80° B.90°C.100° D.110°
3.如图，四边形ABCD中，点E在BC上,∠A+∠ADE=180°，∠B=78°，∠C=60°，求∠EDC的度数．