浙江省金华市2024年七年级上学期期末数学模拟试卷2套【附参考答案】

这是一份浙江省金华市2024年七年级上学期期末数学模拟试卷2套【附参考答案】，共17页。试卷主要包含了下列各变形中，错误的是（，分针转动的角度为 ，【答案】－6；0.7，【答案】解，【答案】①③， 的倒数是，下列关于的说法中，正确的是（，如图， ，等内容，欢迎下载使用。
被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST 的反射面总面积约为 250000m2．将
250000 用科学记数法可表示为（）
A． B． C． D．
“a 的算数平方根”表示为（ ）
A． B． C． D．
如图，某污水处理厂要从 A 处把处理过的水引入排水渠PQ，为了节约用料，铺设垂直于排水渠的管道AB．其中蕴含的数学原理（ ）
两点确定一条直线B．两点之间，线段最短
C．过一点可以作无数条直线D．垂线段最短
x
1
2
3
4
－2
－1
0
1
1
－1
－3
－5
多项式 和 （m，1 为实数，且m≠0）的值由x 的取值决定，下表是当 x 取不同值时多项式对应的值，则关于 x 的方程 的解是（ ）
A．x＝1B．x＝2C．x＝3D．x＝4
《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有共买物，人出八，盈三：人出七，不足四．问人数、物价各几何？意思是：现有几个人共买一件物品，每人出 8 钱，多出 3 钱；每人出 7 钱，还差 4 钱．问人数、物价各是多少？设人数是 x 人，根据题意列一元一次方程，正确的是（ ）
A．8x-3=7x+4B．8x+3=7x-4C．8x-3=7x-4D．8x+3=7x+4
4．下列各变形中，错误的是（
）
A．若a＝b，则ac＝bc
C．若a＝b，则
B．若a＝b，则a＋c＝b＋c
D．若ac＝bc，则a＝b
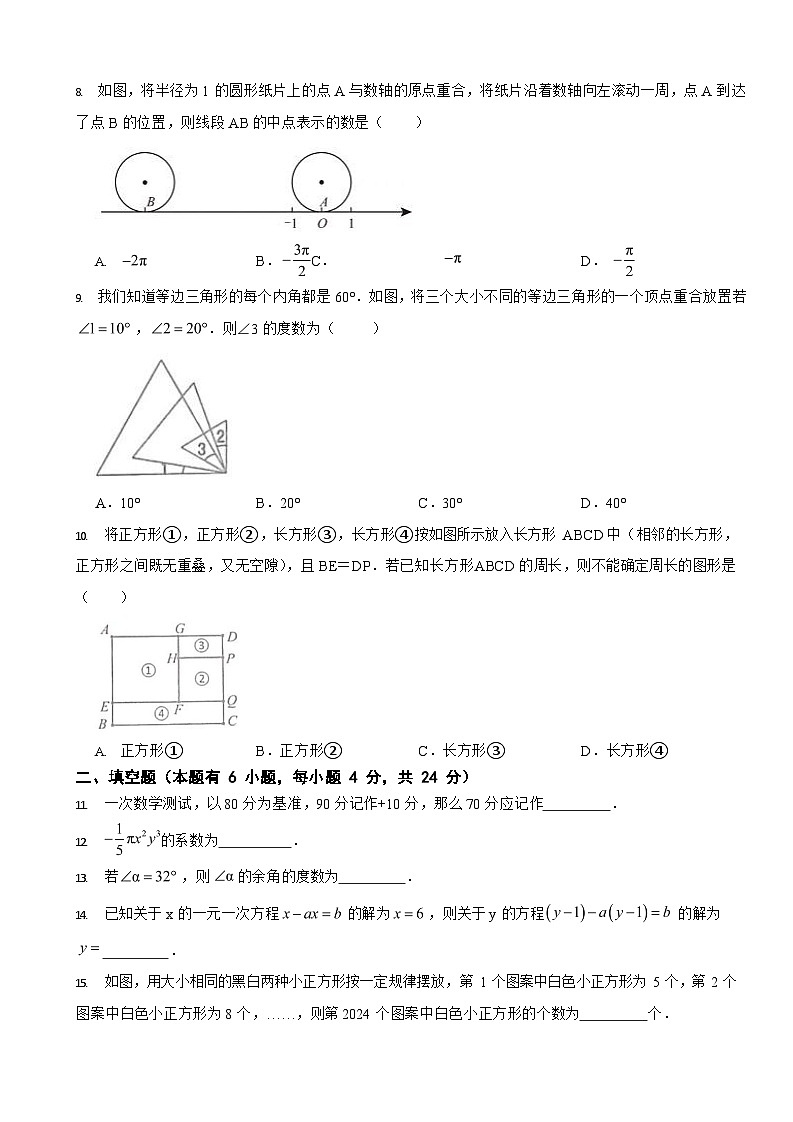
如图，将半径为 1 的圆形纸片上的点A 与数轴的原点重合，将纸片沿着数轴向左滚动一周，点A 到达了点B 的位置，则线段 AB 的中点表示的数是（）
B． C．D．
我们知道等边三角形的每个内角都是 60°．如图，将三个大小不同的等边三角形的一个顶点重合放置若 ， ．则∠3 的度数为（）
A．10°B．20°C．30°D．40°
将正方形①，正方形②，长方形③，长方形④按如图所示放入长方形 ABCD 中（相邻的长方形， 正方形之间既无重叠，又无空隙），且 BE＝DP．若已知长方形ABCD 的周长，则不能确定周长的图形是
（）
正方形①B．正方形②C．长方形③D．长方形④
二、填空题（本题有 6 小题，每小题 4 分，共 24 分）
一次数学测试，以 80 分为基准，90 分记作+10 分，那么 70 分应记作．
的系数为．
若 ，则的余角的度数为．
已知关于x 的一元一次方程的解为，则关于y 的方程 的解为
．
如图，用大小相同的黑白两种小正方形按一定规律摆放，第 1 个图案中白色小正方形为 5 个，第 2 个
图案中白色小正方形为 8 个，……，则第 2024 个图案中白色小正方形的个数为个．
，
，
已如 x 是一个有理数，我们把不超过 x 的最大整数记作 ．例如，．因此， ， ， ，所以有 ，其中．
（1）若，则 ，a＝．
（2）已知 ．则x=．
三、解答题（本题有 8 小题，共 66 分）
计算：
小明同学计算过程如下：原式
请你判断小明的计算过程是否正确，若不正确，请你给出正确的计算过程．
把下列各数的序号填在相应的数集内：
①1；②；③0；④ ；⑤0.25：⑥ ．
整数集合{}；
分数集合{}；
无理数集合{}．
如图，在同一平面内有 4 个点小、B、C．D，请按要求完成下列问题．（不要求写出画法和结论）
连结线段AB，线段AD．
作直线BD，射线AC，两线相交于点 O．
比较大小：AB＋ADBD，理由是．
、
，
A、B、C．D 四个车站的位置如图所示，车站 B 距车站A、D 的距离分别为车站C 与车站D 的距离为．其中a，b 是不为 0 的实数．
求B、C 两站之间的距离（用含 a、b 的代数式表示）．
若B、D 两个车站之间的距离比 A、B 两个车站之间的距离长 8km，求出B、C 两个车站相距多少km？
如图，直线 ，相交于点 ， 和 互余， .
求 的度数；
若 ，求的度数.
七（1）班和七（2）班在晨光文具店为班级的每个同学购买同一款礼品盲盒作为参加研学活动的纪念品．已知两个班级的学生共 90 人，其中七（1）班的学生数超过七（2）班的学生数，两个班的学生数都
不少于 40 人，且不多于 50 人文具店给出该礼品盲盒的价格表如下：
如果两个班级单独购买礼品官盒，购买的数量与学生数相同，那么一共应付 492 元．
若两个班联合购买礼品盲盒，则比各自购买礼品盲盒共可节省多少元？
七（1）班和七（2）班各有多少名学生？（列方程求解）
如果七（1）班有 5 名学生因故不能参加研学活动，七（2）班全体同学参加，请你为这两个班级设计一种最省钱的购买礼品盲盒方案，并计算两个班级购买礼品盲盒的总费用。
根据以下素材，探索完成任务．
购买礼品盲盒的数量
1~44 个
45~86 个
87 个及以上
每个礼品盲盒的价格
6 元
5 元
4 元
时钟里的数学问题
素材1
时钟是我们口常生活中常用的生活用品。钟表上的时针和分针都绕其
轴心旋转，如图．表盘中 1-12 匀分布，分针 60 分钟转动一周是 360°，
时针 60 分钟移动一周的 是 30°，这样，分针转速为每分钟转 6 度，
时针转速为每分钟转 0.5 度．
如图，在数轴上有两个长方形 ABCD 和EFGII， ， ，点A、B、E、F 都在效轴上点A、点 E 表示的数分别为 m、n，且满足 ．长方形 ABCD 以每秒 2 个单位长度的速度沿数轴向右运动，同时长方形 EFGH 以每秒 1 个单位长度的速度沿数轴向左运动，设运动时间为t 秒，运动后的长方形分别记为长方形 与长方形 ．
点B 表示的数为，点F 表示的数为．
当 时，求t 的值．
在运动过程中，两个长方形会出现重叠部分，设重叠部分的面积为 S．
①S 的最大值为．持续的时间为秒：
②当 时，点”所表示的数为．
素材2
当时钟显示 10：10 时（如图）．时针与分针所成角度多少度？解决这个问题，可以先考虑 10：00 时，时针与分针所成角度为 60°；从 10： 00 到 10：10．分针转动的角度为 ．时针转动的角度为
， ．因此 10 点 10 分时，时针与分针所
成角度是 115°．
素材3
当时针和分针所成角度 180°时，我们将这样的时刻称为“美妙时刻”。如图．当时钟显示 6：00 时，此时，时针和分针所成角度 180°，因此6：00 就是一个美妙时刻．
解决问题
任务
1
当时钟显示 1：10 分时，求时针与分针所成角度．
任务
2
时钟显示 1：00 时，时针与分针所成角度为 30°，在 1：00 到 1：30 的 30 分钟内，小明发现存在着时针和分针册直的情况，请求出此时的时刻。
任务
3
6：00 之后的下一个美妙时刻是▲，
一天 24 个小时内，共有▲个美妙时刻。
答案
【答案】A
【答案】A
【答案】C
【答案】D
【答案】D
【答案】B
【答案】A
【答案】C
【答案】C
【答案】B
【答案】-10
【答案】
【答案】
【答案】7
【答案】6074
16．【答案】（1）－6；0.7
（2）－2 或
17．【答案】解：不正确正确解答如下：
18．【答案】（1）①③
（2）②⑤
（3）④⑥
【答案】（1）解：见解析；
解：见解析；
；两点之间线段最短
【答案】（1）解： ，
B、C 两站的距离为.
（2）解：由题意，得 ，
，即
答：B、C 两个车站之间的距离是 4km．
【答案】（1）解：∵∠BOD 和∠AON 互余，
∴∠BOD+∠AON=90°，
∵∠AON=∠COM，
∴∠BOD+∠COM=90°，
∴∠MOB=180°-（∠BOD+∠COM）=90°
（2）解：设∠COM=x，则∠BOC=5x，
∴∠BOM=4x，
∵∠BOM=90°，
∴4x=90°， 解得x=22.5°，
∴∠BOD=90°-22.5°=67.5°.
【答案】（1）解： 元，共可以节省 132 元
解：设七（1）班有学生x 人，则七（2）班有学生 人， 则， ， ，根据题意，得，解得
答：七（1）班有学生 48 人，则七（2）班有学生 42 人
解：七（1）班需购买礼品盲盒 43 个，七（2）班需购买礼品盲盒 42 个，
∴七年级有学生 43+42=85（人），
购买方案 1：若两个班级联合购买盲盒，则需要（43+42）×5=425（元） 购买方案 2：若两个年级各自购买服装，则需要（43+42）×6=510（元）
购买方案 3：若两个年级联合购买 91 套服装，则需要（43+42+2）×4=348（元）
∴最省钱的购买方案为：两个班级一共购买 87 个，费用为 348 元．
【答案】解：任务一： 当时钟显示 11：10 时，时针与分针所成角度为 85°任务二：设 1 点x 分时， 时针与分针垂直，
由题意，得，
解得
答：所求的时间为（也可写成 1 时分）．
（写成 1：22 或 1 时 22 分不扣分）
任务三：下一个美妙时刻是 （也可写成 1 时 分）
（写成 7：05 或 1 时 5 分不扣分） 共有 22 个美妙时刻．
24．【答案】（1）－5；14
解： 或 3
（3）15；；3 或 9
七年级上学期数学期末试卷
一、选择题（共 10 小题，满分 30 分，每小题 3 分）
1． 的倒数是（）
B．C． D．
光明科学城规划总面积达 99000000 平方米，将对标全球最高标准、最好水平.其中 99000000 用科学记数法表示为（）
A． B． C． D．
B． C． D．
若代数式 的值为，则 的值为（）
A．12B．4C．D．
若 的值比 的值小 1，则 的值为（）
B．C．D．
将一副三角板按下列图示位摆放，其中 的是（）
B．
C．D．
3．下列关于的说法中，正确的是（
）
A． 是有理数
B．
是 2 的算术平方根
C． 不是实数
D．
不是无理数
4．单项式 的系数和次数分别是（
）
A． ，1B． ，2
5．如图， ，
C．
，则
，1D． ，2
的度数是（）
《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七， 不足四．问人数，物价各几何？译文为：现有一些人共同买一个物品，每人出 8 元，还盈余 3 元；每人出 7元，则还差 4 元，问共有多少人？这个物品的价格是多少？设共有 人，则可列方程为（ ）
A． B．
C． D．
如图，第 1 个图形中有 1 个三角形，第 2 个图形中有 5 个三角形，第 3 个图形中有 9 个三角形，第
10 个图形中有（）个三角形．
A．37B．38C．39D．40
二、填空题（共 6 小题，满分 24 分，每小题 4 分）
11．2022 年 12 月 1 日，上虞迎来年度第一场雪，早上的温度是 ，中午上升到 ，到夜间又下降了 ，则这天夜间的温度是 ．
12． 的立方根是.
单项式 的系数是，次数是．
若 是关于 的方程 的解，则 的值是．
如图，已知线段AB＝8，延长BA 至点C，使AC＝ AB，D 为线段BC 的中点，则AD＝.
如图，已知 ，射线 从 出发，以每秒 的速度在 内部绕 点逆时针旋转， 若 和 中，有一个角是另一个角的 2 倍，则运动时间为秒.
三、解答题（共 8 小题，满分 66 分）
计算： ．
已知一个正数 的平方根为 和 ．
（1）求的值；
（2） ，的平方根是多少？
如图，平原上有 A，B，C，D 四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池．
不考虑其他因素，请你画图确定蓄水池 H 点的位置，使它到四个村庄距离之和最小；
计划把河水引入蓄水池H 中，怎样开渠最短并说明根据．
已知 ， .
化简：.
当 ， 时，求代数式的值.
解下列方程：
（1） ．
（2） ．
店铺名
优惠信息
是否包邮
甲
任买一件商品先享受九折优惠，同时参加平台每满 200 减 30 元活动
是
乙
购物满 500 元即可使用一张 60 元的店铺优惠券（每人限用一张），
同时参加平台每满 300 元减 50 元活动
是
丙
若购买数量不超过 10 个，则不打折；
若购买数量超过 10 个但不超过 50 个，则超过 10 个部分打九折；
若购买数量超过 50 个但不超过 100 个，则超过 50 个部分打八折；
若购买数量超过 100 个，则超过 100 个部分打七折． 注：不参加平台满减活动．
是
22．2022 年天猫平台“双十一”促销活动如火如荼地进行．小明发现天猫平台甲、乙、丙三家店铺在销售同一款标价均为 30 元的杯子，但三家的促销方式不同，具体优惠信息如下：
若小明想买 25 个该款杯子，请你帮小明分别计算一下甲、乙、丙三家店铺优惠后的实际价格， 再挑选哪家店铺购买更优惠．
若小明想从丙店铺购买 个 该款杯子，请用含 的代数式表示优惠后购买的总价．
若小明想花费 3000 元在丙店铺来购买该款杯子，且恰好用完，则他能买多少个该款杯子？
（注 假设小明均一次性购买）
如图，已知数轴上，两点对应数分别为和 4，为数轴上一动点，对应数为 ．
若为线段的三等分点，求点对应的数．
数轴上是否存在点，使点到点、点距离之和为 10？若存在，求出 的值；若不存在， 请说明理由．
若点、点和点（点在原点）同时向左运动，它们的速度分别为 1 个单位长度 分、2 个单位长度 分和 1 个单位长度 分，则经过多长时间点为的中点？
如图 1，将两块直角三角板（一块含有 、角，另一块含 角）摆放在直线 上，三角板
绕点 以每秒 的速度逆时针旋转．当 第一次与射线 重合时三角板 停止转动，设旋转时间为 秒．
当 时，求 和 的度数；
如图 2，若两块三角板同时旋转，三角板 以每秒 的速度绕点 顺时针旋转，当 第一次与射线 重合时三角板 立即停止转动．
①用含 的代数式表示射线 和射线 重合前 和 的度数；
②整个旋转过程中，当满足 时，求出相应的 的值．
答案
【答案】C
【答案】A
【答案】B
【答案】D
【答案】C
【答案】D
【答案】D
【答案】A
【答案】B
【答案】A
【答案】
【答案】-4
【答案】；3
【答案】
【答案】2
【答案】3 或 6
【答案】解：
．
【答案】（1）解：正数的平方根为 和 ，这两个数互为相反数或表示同一个数，
或 ，
解得： 或
解得： 或；
（2）解： ，
， ， ，
， ， ，
，
的平方根是．
【答案】（1）解：由两点之间线段最短可知，连接 AD、BC 交于H，则H 为蓄水池位置；
（2）解：根据垂线段最短可知，要做一个垂直 EF 的线段．
⑴连结 ， ，交于点 ，则 为所求的蓄水池点．
⑵过作于，沿开挖，可使开挖的渠最短，依据是：“点与直线的连线中，垂线段最短”．（如图）
【答案】（1）解：
.
（2）解：当 ， 时，
多项式
【答案】（1）解： ，
，
，
；
（2）解：，
， ，
，
，
．
【答案】（1）解：甲： （元 ， 乙： （元 ，
丙： （元 ，
因为 ，所以挑选甲店铺更优惠． 答：甲店铺更优惠．
（2）解：由题意可得：
（元 ．
答：购买总价为 元．
（3）解：由（2）可知，令 ，
解得： ．
答：他能买 120 个该款杯子．
【答案】（1）解：为线段的三等分点，且点、的对应的数分别为，4， 点对应的数为 0，2．
解：存在．
设点 对应的数为 ，
点到点、点距离之和为 10，
①当点P 在A 左侧，
，
∴ ，
②当点P 在B 右侧，
，
∴ ，
③当点P 在AB 中间，此情况不存在， 解得： 或 ．
解：设经过 分点为的中点，
由题意得： ，
解得： ，
即经过 2 分钟点为的中点．
【答案】（1）解：如图 1， ，
，
当 时，三角板 绕点 逆时针旋转， 与 减小的度数相同为： ，
故 ，
；
（2）解：①由图 1，得 ， 设运动时间为，如图 2，
， ， ， ，
①当时，
， ， ， ，
，
；
②当 时，
， ；
③当时，
， ；
② ，
，
， ，
，
故不存在 的值；
①当 时，如图：
， 故不存在 的值；
②当 时，如图：
，
，
，
，
解得，，
综上所述， 的值为或．