初中数学人教版（2024）九年级下册27.2.1 相似三角形的判定优质课ppt课件

这是一份初中数学人教版（2024）九年级下册27.2.1 相似三角形的判定优质课ppt课件，文件包含人教版九年级下册数学27212相似三角形的判定第二课时课件pptx、人教版九年级下册数学27212相似三角形的判定第二课时教案docx、人教版九年级下册数学27212相似三角形的判定第二课时分层练习docx、人教版九年级下册数学27212相似三角形的判定第二课时导学案docx、人教版九年级下册数学27212相似三角形的判定第二课时预习案docx等5份课件配套教学资源，其中PPT共49页， 欢迎下载使用。
1、掌握“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似 ”“三边对应成比例，两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定方法．并能运用这三个判定定理证明两个三角形相似。2、结合全等三角形的SSS和SAS的证明方法，通过类比观察、猜想、证明等活动，探索相似三角形判定定理证明的过程，体会转化的数学思想。3、进一步积累研究几何图形问题的经验。
如果三角分别相等、三边成比例的两个三角形叫做相似三角形.
定义法：对应角相等，对应边成比例的两个三角形相似.
三角形全等的判定方法有五种：1. 边边边（SSS）：三边对应相等的两个三角形全等。2. 边角边（SAS）：两边和它们的夹角分别相等的两个三角形全等。3. 角边角（ASA）：两角和它们的夹边分别相等的两个三角形全等。4. 角角边（AAS）：两个角和其中一角的对边对应相等的两个三角形全等。5. 斜边直角边（HL）：斜边和一条直角边对应相等的两个直角三角形全等。
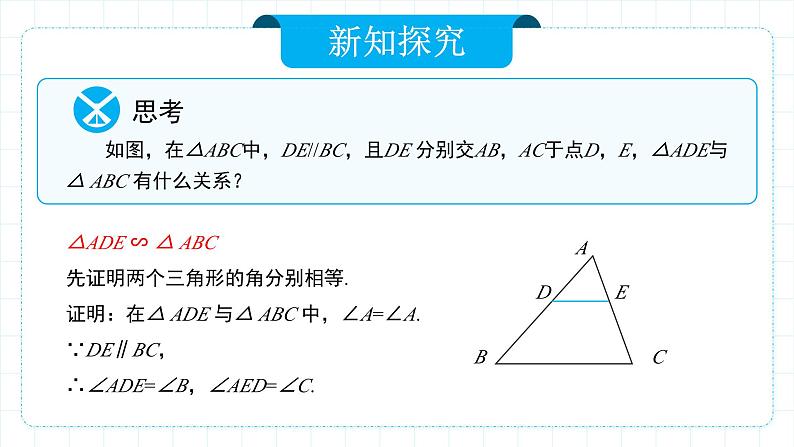
△ADE ∽ △ ABC 先证明两个三角形的角分别相等.证明：在△ ADE 与△ ABC 中，∠A=∠A.∵DE∥BC， ∴∠ADE=∠B，∠AED=∠C.
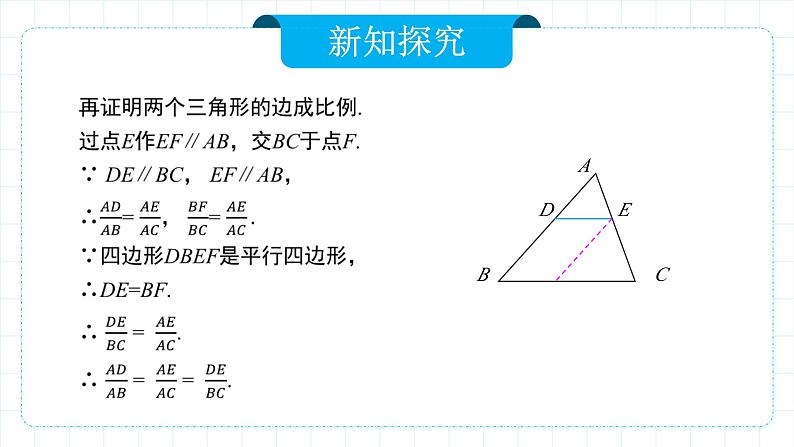
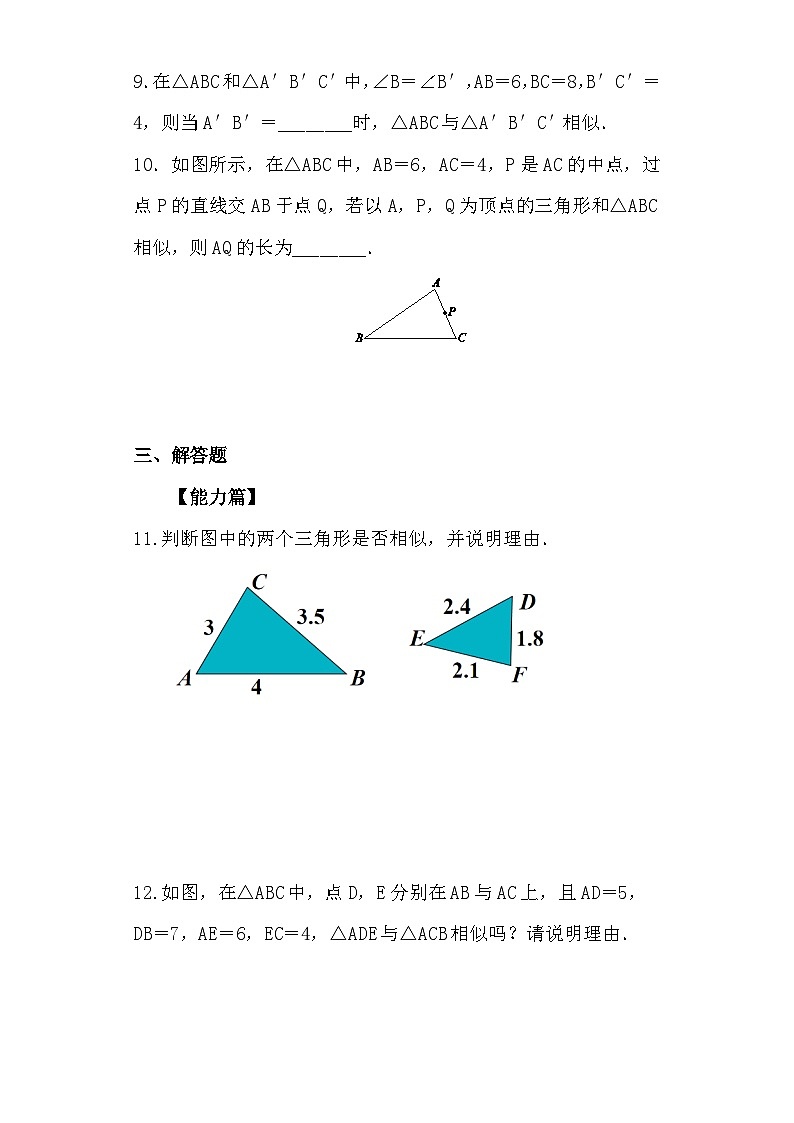
这样，我们证明了△ADE 和△ABC 的角分别相等，边成比例，所以△ADE ∽△ABC .因此，我们有如下判定三角形相似的（预备）定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
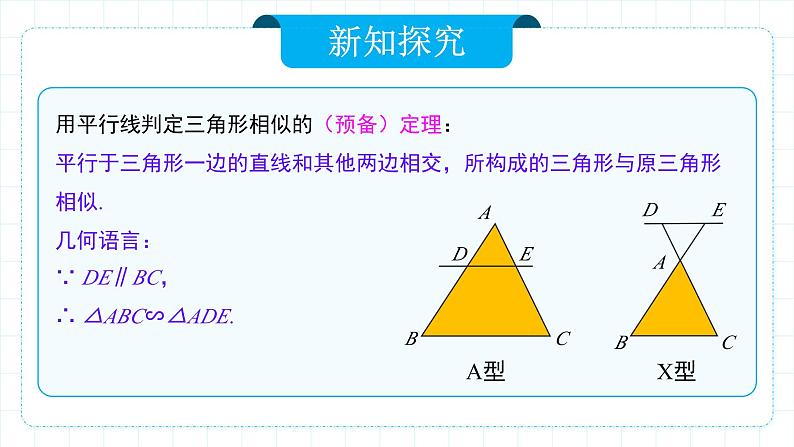
用平行线判定三角形相似的（预备）定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.几何语言：∵ DE∥BC，∴ △ABC∽△ADE.
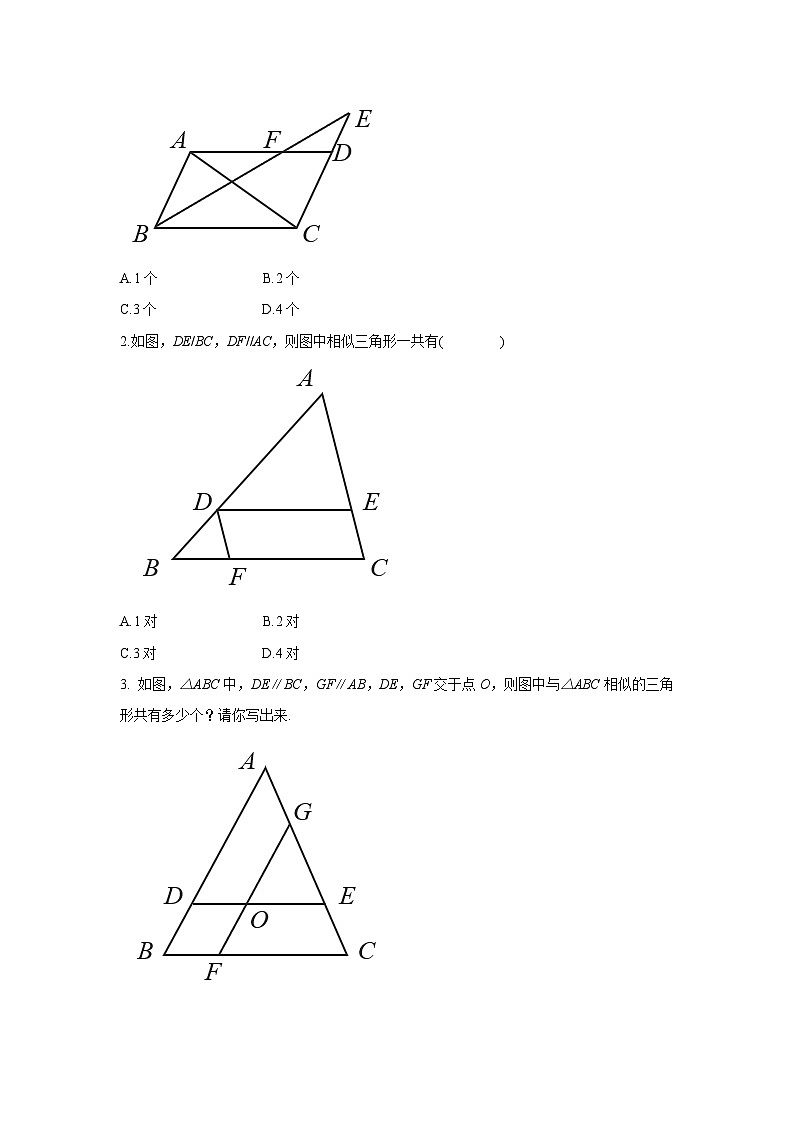
1.如图，在平行四边形ABCD中，F是AD边上的任意一点，连接BF并延长交CD的延长线于点E，则图中与△DEF相似的三角形共有( )A.1个 B.2个C.3个 D.4个解析：由于四边形ABCD是平行四边形，因此FD//BC，DE//AB.于是可从图中找出符合“A”型相似的△DEF与△ CEB，符合“X”型相似的△DEF与△ ABF.故选B.
2.如图，DE/BC，DF//AC，则图中相似三角形一共有( )A.1对 B.2对C.3对 D.4对
3. 如图，△ABC中，DE∥BC，GF∥AB，DE，GF交于点O，则图中与△ABC相似的三角形共有多少个？请你写出来.解：与△ABC相似的三角形有3个：△ ADE△ GFC △ GOE
2. 如图，在△ABC中，DE∥BC，且AD=3，DB=2.写出图中的相似三角形，并指出其相似比.
解： △ADE ∽ △ABC，相似比为3:5.
类比三角形全等的判定方法(SSS)，我们能不能通过三边来判定两个三角形相似呢？
想一想：改变k值大小，结论是否依然成立？
依然成立。△ABC ∽△A′B′C′.
△ A′ DE是证明的中介，它把 △ABC 和△A′B′C′联系起来.
由此我们得到利用三边判定三角形相似的定理(如图)：三边成比例的两个三角形相似.
类比判定三角形全等的SAS方法，能不能通过两边和夹角来判定两个三角形相似呢？
△ABC和△A′ B′ C′不一定相似.
应用该定理判定两个三角形相似时，相等的角必须是成比例的两边的夹角.
1.如图，已知 △ABC中，D 为边 AC 上一点，P 为边AB上一点，AB=12，AC=8，AD=6，当AP的长度为 时，△ADP和△ABC相似.解析：当 △ADP ∽ △ACB时，AP：AB=AD：AC，AP：12 =6：8 ，解得 AP=9；当△ADP ∽ △ABC时， AD：AB=AP：AC， ∴ 6：12=AP：8，解得 AP =4. ∴当 AP 的长度为 4或9时， △ADP和△ABC相似.
例1 根据下列条件，判断△ABC 与△A′B′C′是否相似，并说明理由：(1) AB=4cm，BC=6 cm，AC=8 cm， A′B′ =12 cm， B′C′ =18 cm，A′C′ =24 cm；
例1 根据下列条件，判断△ABC 与△A′B′C′是否相似，并说明理由： (2)∠A =120°，AB=7 cm，AC=14 cm， ∠A′ =120°， A′ B′ =3 cm， A′ C′ =6 cm.
1.根据下列条件，判断△ABC与△ A′B′C′是否相似，并说明理由：(1)∠A = 40°，AB=8 cm，AC=15 cm， ∠ A′ = 40°，A′B′ =16 cm， A′C′ =30 cm；(2) AB=10cm， BC=8 cm，AC=16 cm， A′B′ =16 cm,，B′C′ =12.8 cm， A′C′ =25.6 cm.
1.根据下列条件，判断△ABC与△ A′B′C′是否相似，并说明理由：(1)∠A=40°，AB=8 cm，AC=15 cm，∠ A′ =40°，A′B′ =16 cm， A′C′ =30 cm；(2)AB=10cm，BC=8 cm，AC=16 cm，A′B′ =16 cm,，B′C′ =12.8 cm， A′C′ =25.6 cm.
2.图中的两个三角形是否相似？为什么？
3.要制作两个形状相同的三角形框架，其中一个三角形框架的三边长分别为4cm，5cm和6cm，另一个三角形框架的一边长为2cm，它的另外两条边长应当是多少？你有几种制作方案？
1.已知：点D，E，F分别是△ABC三边的中点. 求证：△EFD∽△ABC.
2. 如图，D 是 △ABC 一边 BC 上一点，连接 AD，使△ABC ∽ △DBA的条件是 （ ） A. AC : BC=AD : BD B. AC : BC=AB : AD C. AB2 = CD · BC D. AB2 = BD · BC
3. 在 △ABC 和 △DEF 中，∠C =∠F=70°，AC = 3.5 cm，BC = 2.5 cm，DF =2.1 cm，EF =1.5 cm. 求证：△DEF∽△ABC.
4. 如图，△ABC 与 △ADE 都是等腰三角形，AD=AE， AB=AC，∠DAB=∠CAE. 求证：△ABC ∽△ADE.