人教版（2024）九年级下册27.2.3 相似三角形应用举例完美版ppt课件

这是一份人教版（2024）九年级下册27.2.3 相似三角形应用举例完美版ppt课件，文件包含人教版九年级下册数学2723相似三角形应用举例课件pptx、人教版九年级下册数学2723相似三角形应用举例教案docx、人教版九年级下册数学2723相似三角形应用举例分层练习docx、人教版九年级下册数学2723相似三角形应用举例导学案docx、人教版九年级下册数学2723相似三角形应用举例预习案docx等5份课件配套教学资源，其中PPT共60页， 欢迎下载使用。
1.进一步巩固相似三角形的知识，学会用相似三角形解决不能直接测量的物体的长度和高度等一 些实际问题.2.通过把实际问题转化为有关相似三角形的模型，进一步体会数学建模的思想方法.3.培养学生分析问题、解决问题能力，增强观察、归纳、建模、应用能力，在活动中也培养学生良好的情感态度，主动参与、合作交流意识.
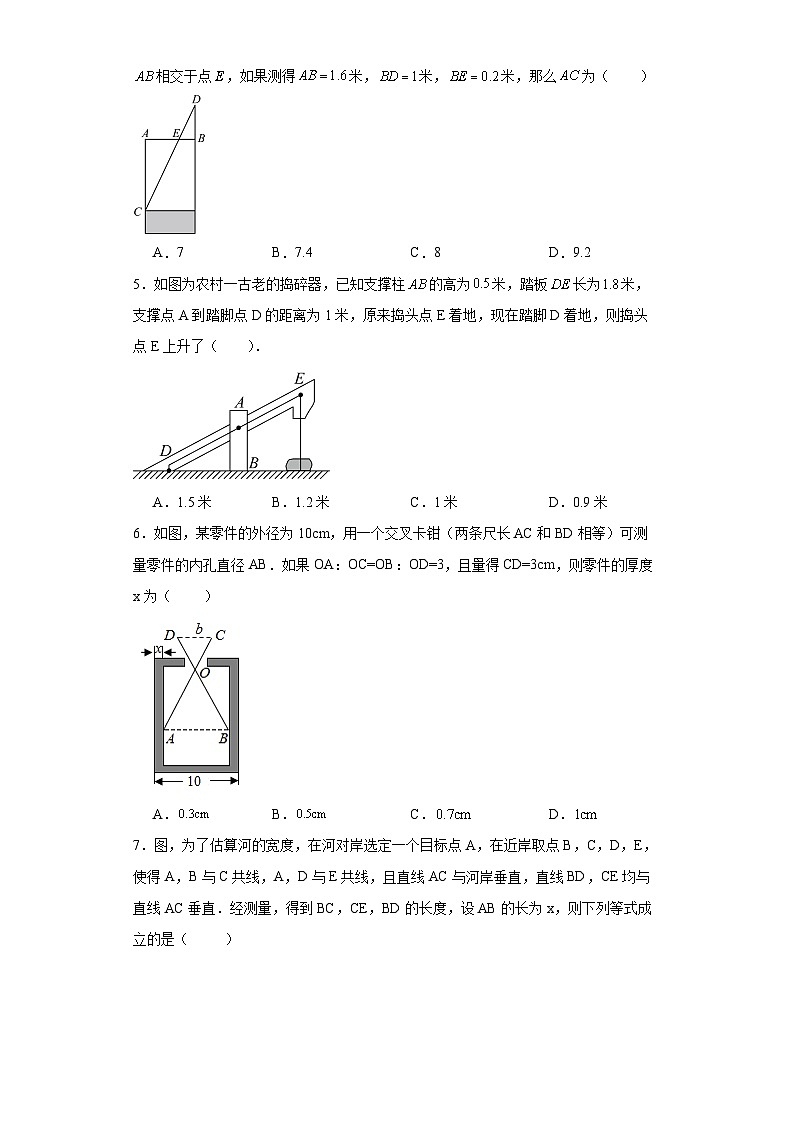
如何判断两个三角形是否相似？
(1) 定义法： 对应角相等，对应边成比例的两个三角形相似.(2) 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似.(3) 三边成比例的两个三角形相似.(4) 两边成比例且夹角相等的两个三角形相似.(5) 两角分别相等的两个三角形相似.(6) 斜边和一条直角边成比例的两个直角三角形相似.
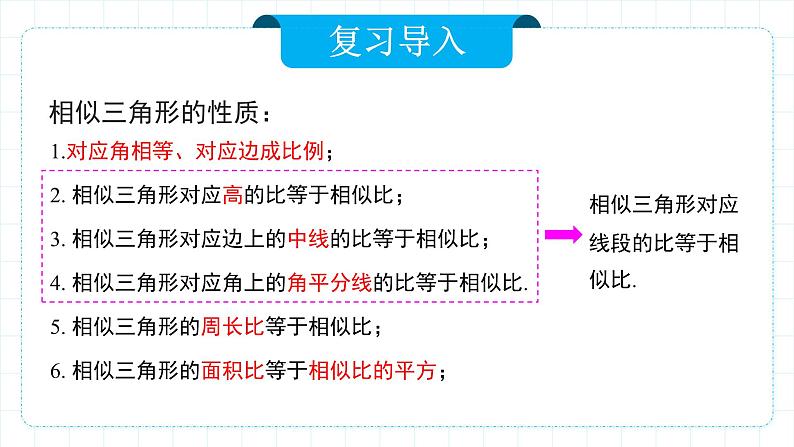
1.对应角相等、对应边成比例；2. 相似三角形对应高的比等于相似比； 3. 相似三角形对应边上的中线的比等于相似比；4. 相似三角形对应角上的角平分线的比等于相似比.5. 相似三角形的周长比等于相似比；6. 相似三角形的面积比等于相似比的平方；
相似三角形对应线段的比等于相似比.
一、利用相似三角形测量高度.
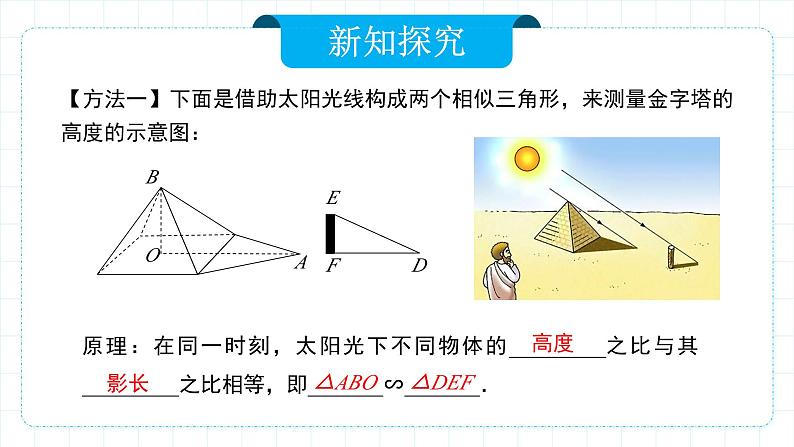
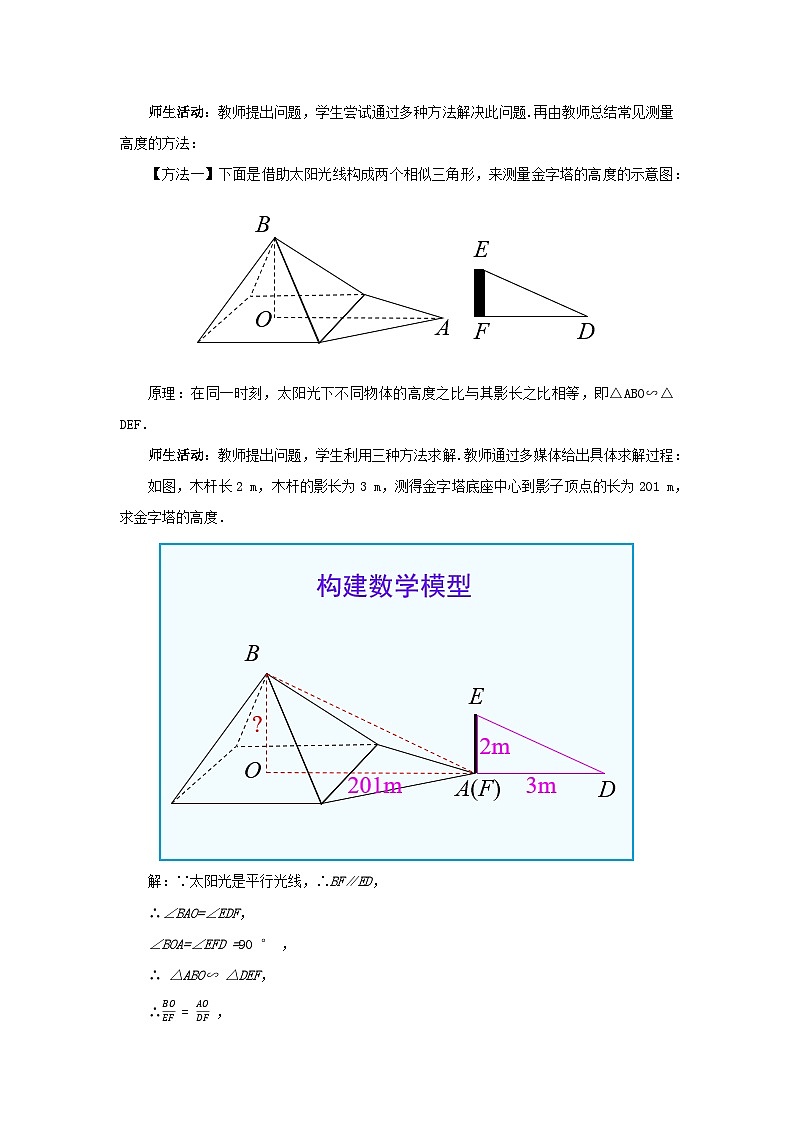
【方法一】下面是借助太阳光线构成两个相似三角形，来测量金字塔的高度的示意图：
原理：在同一时刻，太阳光下不同物体的_________之比与其_________之比相等，即_______∽_______．
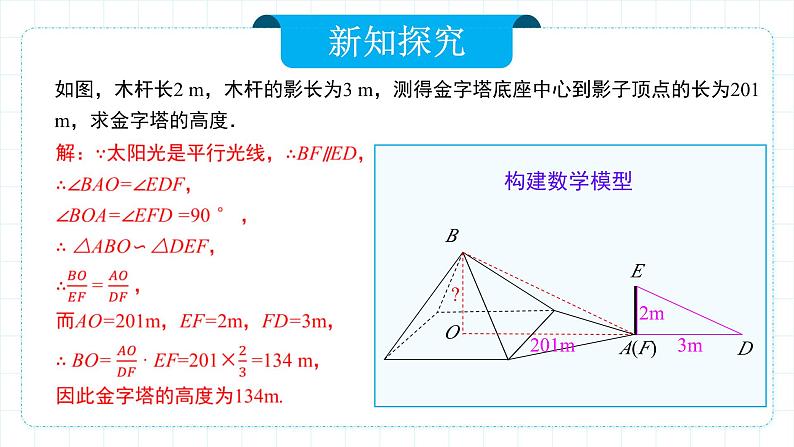
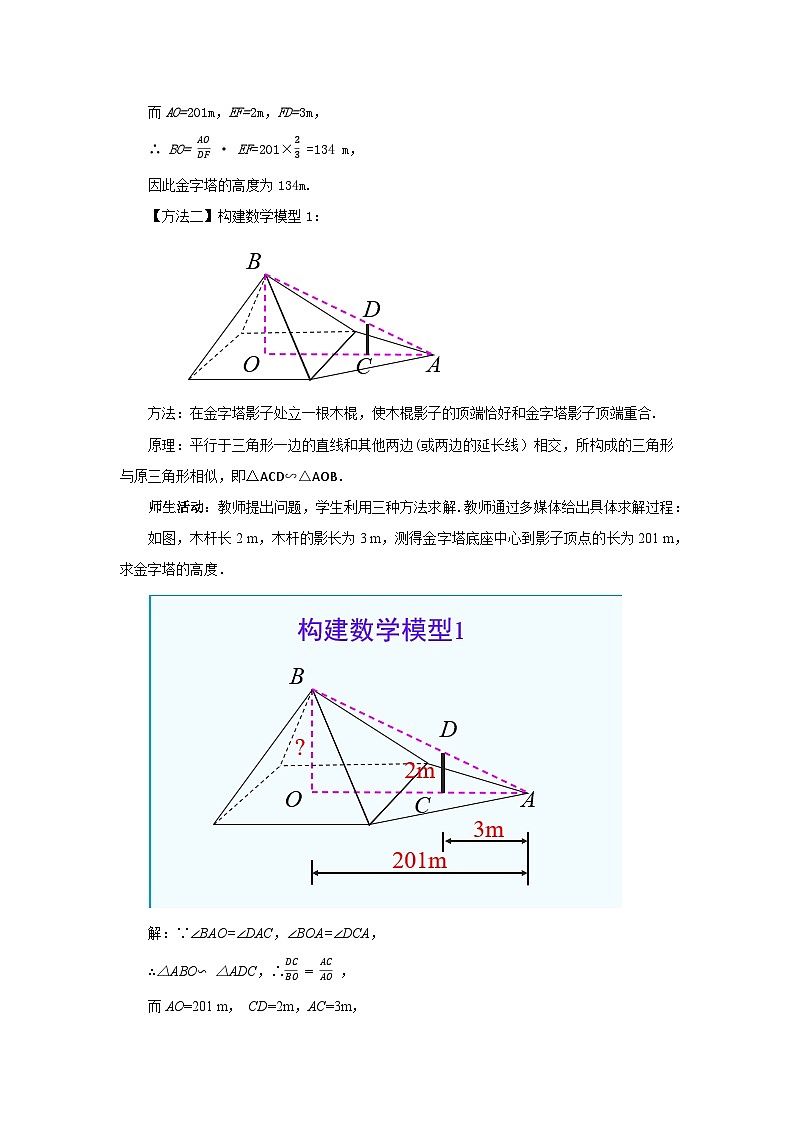
如图，木杆长2 m，木杆的影长为3 m，测得金字塔底座中心到影子顶点的长为201 m，求金字塔的高度．
方法：在金字塔影子处立一根木棍，使木棍影子的顶端恰好和金字塔影子顶端重合.原理：________三角形一边的直线和其他两边(或两边的延长线）相交，所构成的三角形与原三角形相似，即_______∽_______．
【方法二】构建数学模型1：
原理：利用光的反射定律，______等于______，可以通过 证明_______∽_______．
【方法三】构建数学模型2：
∠EAF=∠BAO，∠EFA=∠BOA
1．《孙子算经》是中国古代重要的数学著作．其中有首歌谣：今有竿不知其长，量得影长一丈五尺．立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸(提示：1丈＝10尺，1尺＝10寸)，问竹竿长为几丈几尺？
2. 如图，小明为了测量一棵树CD的高度，他在距树24m处立了一根高为2m的标杆EF，然后小明前后调整自己的位置，当他与树相距27m的时候，他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m，求树的高度.
解析：人、树、标杆是相互平行的，添加辅助线，过点A作AN∥BD交CD于N，交EF于M，则可得△AEM∽△ACN.
3. 如图，为了测量一栋楼的高度OE，小明同学先在操场上A处放一面镜子，向后退到B处，恰好在镜子中看到楼的顶部 E；再将镜子放到 C处，然后后退到 D处，恰好再次在镜子中看到楼的顶部 E(O，A，B，C，D在同一条直线上) ，测得AC=2m，BD=2.1m，如果小明眼睛距地面高度 BF，DG 为1.6 m，试确定楼的高度 OE.
4.如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DF＝50cm，EF＝30cm，测得边DF离地面的高度AC＝1.5m，CD＝20m，求树高AB？
二、利用相似三角形测量宽度.
例5 如图，为了估算河的宽度，我们可以在河对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S 共线且直线 PS 与河垂直，接着在过点S且与PS垂直的直线a上选择适当的点T，确定PT与过点Q且垂直PS的直线b的交点R．已测得QS=45 m，ST=90 m，QR=60 m，请根据这些数据，计算河宽PQ．
【方法一】构建数学模型：原理：________三角形一边的直线和其他两边(或两边的延长线）相交，所构成的三角形与原三角形相似，即_______∽_______．
想一想，还有其它方法求河宽吗？
【方法二】构建数学模型：原理：________分别相等的两个三角形相似，可以通过 . 证明_______∽_______．
如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点 A，再在河的这一边选点 B 和 C，使 AB⊥BC，然后，再选点 E，使 EC ⊥ BC ，用视线确定 BC 和 AE 的交点 D． 此时如果测得 BD＝80 m，DC＝30 m，EC＝24 m，求两岸间的大致距离 AB．
∠ABD=∠DCE，∠ADB=∠CDE
如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点 A，再在河的这一边选点 B 和 C，使 AB⊥BC，然后，再选点 E，使 EC ⊥ BC ，用视线确定 BC 和 AE 的交点 D．此时如果测得 BD＝150m，DC＝50m，EC＝40m，求两岸间的大致距离 AB．
1.如图，M，N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞，工程人员为计算工程量，必须计算 M，N两点之间的距离，选择测量点A，B，C，点B，C分别在 AM，AN上，现测得AM=1000米，AN=1800米，AB=54米，BC=45米，AC=30米，求 M，N两点之间的距离.
2.学习相似三角形相关知识后，善于思考的小明和小颖两位同学想通过所学计算桥AF的长.如图，该桥两侧河岸平行，他们在河的对岸选定一个目标作为点A，再在河岸的这一边选出点B和点C，分别在AB、AC的延长线上取点D、E，使得DE∥ BC，经测量，BC=120米，DE=200米，且点E到河岸BC的距离为60米，已知AF⊥BC于点F，请你根据提供的数据，帮助他们计算桥AF的长度.
3. 周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D竖起标杆DE，使得点E与点C、A共线．已知：CB⊥AD，ED⊥AD，测得BC＝1m，DE＝1.5m，BD＝8.5m．测量示意图如图所示．请根据相关测量信息，求河宽AB．
三、利用相似解决有遮挡物问题.
例6 如图，左、右并排的两棵大树的高分别是AB=8 m和CD=12 m，两树底部的距离BD=5 m，一个人估计自己眼睛距地面1.6 m．她沿着正对这两棵树的一条水平直路l从左向右前进，当她与左边较低的树的距离小于多少时，就看不到右边较高的树的顶端C了？
【提示】如图（1），设观察者眼睛的位置 (视点) 为点 F，画出观察者的水平视线 FG，它交 AB，CD 于点 H，K.视线 FA，FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地，∠CFK 是观察点 C 时的仰角，由于树的遮挡，区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 在点E位置时，观察员恰好看到顶端C点，再往前走就根本看不到 C 点了.
如图所示，一段街道的两边缘所在直线分别为AB，PQ，并且AB//PQ.建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N.小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等候小亮.
a.请你在图中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置(用点C标出)；
2.如图，测得BD=120m，DC=60m，EC=50 m，求河宽 AB.
1. 小明身高 1.5 米，在操场的影长为 2 米，同时测得教学大楼在操场的影长为 60 米，则教学大楼的高度应为 ( ) A. 45米 B. 40米 C. 90米 D. 80米
2. 小刚身高 1.7 m，测得他站立在阳光下的影子长为0.85 m，紧接着他把手臂竖直举起，测得影子长为 1.1 m，那么小刚举起的手臂超出头顶 ( ) A. 0.5 m B. 0.55 m C. 0.6 m D . 2.2 m
3. 如图，有点光源 S 在平面镜上面，若在 P 点看到点光源的反射光线，并测得 AB＝10 cm，BC＝20 cm，PC⊥AC，且 PC＝24 cm，则点光源 S 到平面镜的距离 SA 为 .
4. 如图，为了测量水塘边 A、B 两点之间的距离，在可以看到 A、B 的点 E 处，取 AE、BE 延长线上的C、D 两点，使得 CD∥AB. 若测得 CD＝5 m，AD＝15 m，ED=3 m，则 A、B 两点间的距离为 m.
5. 如图，某一时刻，旗杆 AB 的影子的一部分在地面上，另一部分在建筑物的墙面上．小明测得旗杆AB 在地面上的影长 BC 为 9.6 m，在墙面上的影长 CD 为 2 m．同一时刻，小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m．请帮助小明求出旗杆的高度．
解：如图：过点 D 作 DE∥BC，交 AB 于点 E，∴ DE = CB = 9.6 m，BE = CD = 2 m，∵ 在同一时刻物高与影长成正比例，∴ EA : ED=1 : 1.2，∴ AE = 8 m，∴ AB = AE + EB = 8 + 2 = 10 (m)，∴ 学校旗杆的高度为 10 m.
1.（2024·四川广元·中考真题）数学实验，能增加学习数学的乐趣，还能经历知识“再创造”的过程，更是培养动手能力，创新能力的一种手段，小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题，请同学们帮他解决.
在△ABC中，点D为边AB上一点，连接CD.(1)初步探究 如图2，若∠ACD= ∠B，求证：AC2=AD · AB；
在△ABC中，点D为边AB上一点，连接CD.(2)尝试应用 如图3，在(1)的条件下，若点D为AB中点，BC=4，求CD的长；
复习巩固1.有一块三角形的草地，它的一条边长为 25 m，在图纸上，这条边的长为5cm，其他两条边的长都为4cm，求其他两边的实际长度.
2.根据下列条件，判断△ABC 与△A′B′C′是否相似，并说明理由：(1)AB=10 cm，BC=12 cm，AC=15 cm， A′B′ =150 cm， B′C′ =180 cm， A′C′ =225 cm；
2.根据下列条件，判断△ABC 与△A′B′C′是否相似，并说明理由：(2)∠A=70°，∠B=48°，∠A′ =70°，∠C′ =62°.
解：∠C=180°-（70°+48°）=62°∴ ∠A= ∠A′ =70°， ∠C= ∠C′ =62°，∴ △ABC ∽ △A′B′C′.
3.如图，(1)判断两个三角形是否相似；(2)求x和y的值.
4.如图， △ABC中，DE∥BC，EF∥AB，求证△ADE ∽ △ EFC.
证明：∵DE//BC，∵∠AED=∠C，又∵EF // AB. ∴ ∠A=∠CEF，∴ △ADE ∽ △ EFC.
5.如图，△ABC中，DE ∥ FG∥ BC，找出图中所有的相似三角形.
解： △ADE ∽ △ AFG ， △ADE ∽ △ ABC， △ AFG ∽△ ABC，
7. 如图，AD是Rt△ABC斜边上的高，若AB=4cm，BC=10cm，求BD的长.
8.如图，比例规是一种画图工具，它由长度相等的两脚 AD 和BC交叉构成，利用它可以把线段按一定的比例伸长或缩短，如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方(即同时使OA=3OD，OB=3OC)，然后张开两脚，使A，B两个尖端分别在线段l的两个端点上，这时CD与AB 有什么关系？为什么？
9.如图，利用标杆 BE 测量建筑物的高度，如果标杆 BE 高 1.2 m，测得AB=1.6 m，BC=12.4 m，楼高 CD 是多少？
10.如图，为了测量一栋楼的高度，王青同学在她脚下放了一面镜子，然后向后退，直到她刚好在镜子中看到楼的顶部.这时∠LMK 等于∠SMT吗？如果王青身高 1.55 m，她估计自己眼睛距地面1.50 m，同时量得 LM=30 cm，MS=2m，这栋楼有多高?
11.如图，四边形ABCD 是矩形，点F在对角线AC上运动，EF∥BC，FG∥CD，四边形 AEFG 和四边形ABCD 一直保持相似吗？证明你的结论.
12.如图，平行于 BC 的直线 DE 把△ABC 分成面积相等的两部分，试确定点 D(或E)的位置.
14.如图，△ABC中，AB=8，AC=6，BC=9.如果动点D以每秒2个单位长度的速度，从点B出发沿边 BA 向点A 运动，此时直线 DE//BC，交AC 于点E.记x秒时 DE 的长度为y，写出y关于x的函数解析式，并画出它的图象.