福建省福州市连江县2023-2024学年七年级（上）期末数学试卷（解析版）

这是一份福建省福州市连江县2023-2024学年七年级（上）期末数学试卷（解析版），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题
1.的相反数是（ ）
A. B. 2024C. D.
【答案】B
【解析】的相反数是2024，
故选：B．
2. 2023年9月23日晚，杭州亚运会开幕式现场，超过1.05亿名线上火炬手汇聚而成的“数字火炬手”与现场真实的火炬手一起，共同点燃亚运之火，创造了新的吉尼斯世界纪录．其中数据1.05亿用科学计数法可表示为（ ）
A. B. C. D.
【答案】C
【解析】1.05亿，保留1位整数为1.05，小数点向左移动8位，
因此1.05亿，
故选C．
3. 下列实数中，是无理数的是（ ）
A. B. C. D.
【答案】C
【解析】，，是有理数，是无理数
故选：C．
4. 7的平方根的是（ ）
A. B. C. D.
【答案】D
【解析】7的平方根的是
故选：D．
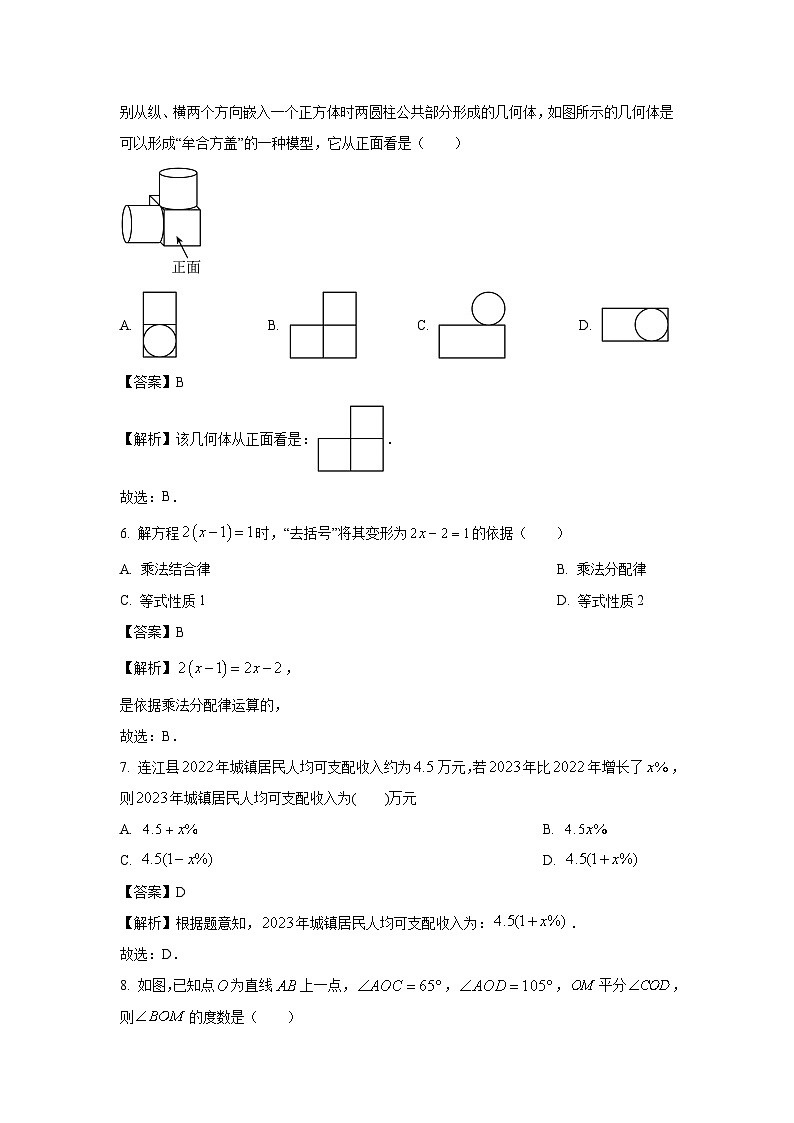
5. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图所示的几何体是可以形成“牟合方盖”的一种模型，它从正面看是（ ）
A. B. C. D.
【答案】B
【解析】该几何体从正面看是：．
故选：B．
6. 解方程时，“去括号”将其变形为的依据（ ）
A. 乘法结合律B. 乘法分配律
C. 等式性质1D. 等式性质2
【答案】B
【解析】，
是依据乘法分配律运算的，
故选：B．
7. 连江县年城镇居民人均可支配收入约为万元，若年比年增长了，则年城镇居民人均可支配收入为( )万元
A. B.
C. D.
【答案】D
【解析】根据题意知，年城镇居民人均可支配收入为：．
故选：D．
8. 如图，已知点为直线上一点，，，平分，则的度数是（ ）

A. B. C. D.
【答案】B
【解析】，
，
，
，
故选：B．
9. 甲组的4名工人3月份完成的总工作量比此月人均定额的4倍多20件，乙组的5名工人3月份完成的总工作量比此月人均定额的6倍少20件．如果甲组工人实际完成的此月人均工作量比乙组的多2件，那么此月人均定额是多少件？小明根据题意，设某个量为未知数，列得方程：．则下列说法错误的是（ ）
A. 未知数的意义是此月人均定额为件
B. 整式的意义是甲组工人的实际人均工作量
C. 整式的意义是乙组工人的实际人均工作量
D. 整式的意义是乙组5名工人实际完成的总工作量
【答案】C
【解析】设此月人均定额为件，
则：，
其中表示甲组工人的实际人均工作量，
表示乙组5工人实际完成总工作量，
表示乙组工人的实际人居工作量，
故A、B、D都是正确的，是不符合题意的，
故选：C．
10. 已知关于的方程的解为，则关于的方程的解为（ ）
A. B. C. 8D. 2
【答案】B
【解析】将代入方程，得，
，
，
，且，
，解得，
故选：B．
二、填空题
11. 的算术平方根是_________．
【答案】
【解析】的平方根是±，的算术平方根是.
故答案为：.
12. 多项式的次数是__________．
【答案】2
【解析】∵多项式中次数最高项的次数是2，
∴多项式的次数是2．
故答案为：2．
13. “的倍与的和等于的与的差”，用等式表示为__________
【答案】
【解析】依题意，得，
故答案为：．
14. 比较大小：_____0.5（用“＞”或“＜”填空）．
【答案】
【解析】，
，即，
，
即，
，
故答案为：
15. 如图，将一副三角板的两直角顶点重合放置，已知，则的余角的度数为__________．

【答案】
【解析】∵
∴，
∴的余角的度数为，
故答案为：．
16. 已知数轴上，，，四点所表示的数分别为，，，，，其中有两个数的和为0，且满足．若，，．则这四个数中互为相反数的是__________．
【答案】，或，
【解析】因为这四个数中有两个数和为0，则一定有一个负数和一个正数，因为，
则这四个数为两个正数和两个负数，即，
若和互为相反数，因为，则，，
若和互为相反数，因为，，
所以，则，，，
若和互为相反数，因为，，
所以，则，，，（舍去）．
故答案为：，或，．
三、解答题
17. 计算：
（1）；
（2）．
解：（1）
（2）
18. 先化简，再求值：，其中，．
解：
，
当，时，
原式
．
19. 解方程：．
解：
去分母，
去括号，
移项，
合并同类项，
化系数为1，
20. 如图，平面上有三个点，，．
（1）根据下列语句按要求画图；
①画直线；
②画射线；
③连接，用圆规在的反向延长线上截取，连接（保留作图痕迹）；
（2）在（1）的作图条件下，__________（填“”“=”或“”），依据是__________．
解：（1）如图，直线，射线，线段即为所求；
；
（2），即（两点之间线段最短）．
故答案为：，两点之间线段最短．
21. 在数轴上，点表示的数，点，点关于原点对称，把点向右移动2个单位得到点，设点表示的数为，点所表示的数为．
（1）数的值是__________；数的值是__________；
（2）求的值．
解：（1）∵点A表示的数，点A，点B关于原点对称，
∴点B表示的数是，
∴，
∵把点A向右移动2个单位得到点C，
∴点C表示的数，
故答案为：，；
（2）∵由（1）可知，，
∴
．
22. 七年级学生小明有一天看到在读八年级的姐姐的作业本上有一道题：求出的值．他想利用目前所学的知识通过推理的方法简便解决这个问题，他发现以下规律：
①
②
③
④
（1）请你写出第⑤个式子：__________；
（2）第（，且为正整数）个式子可以表示为：__________；
（3）运用上述结论，求的值（写出计算过程）．
解：（1）由题意得，第5个式子为．
故答案为：；
（2）结合（1）得第个式子为．
故答案为：；
（3）由（2）得，，
，
则
．
答：值为8088．
23. 如图，已知点，是线段上两点，，是线段的中点，点是线段的三等分点．
（1）若，求的长；
（2）若，求的长．
解：（1）由于，可设，则，，
，
，
，，，
是线段的中点，
，
；
（2）由于，可设，则，，
是线段的中点，
，
，
，即，
解得，
．
24. 某校七年级组织知识竞赛活动，共设选择题40道，各题分值相同．下表记录了5名参赛者的得分情况．
（1）观察表格，请直接填写答对一道题得__________分，答错一道题得__________分，不答一道题得__________分；
（2）参赛者有6道题答错，他得了196分，请问他答对了几道题，不答几道题？
（3）若参赛者有道题不答，他得分为奇数，你认为可能吗？请说明理由．
解：（1）根据参赛者的答题及得分情况可知，
答对一道题得分为：分．
根据参赛者的答题及得分情况可知，
答错一道题的得分为：分．
根据参赛者的答题及得分情况可知，
不答一道题的得分为：分．
故答案为：，，．
（2）设参赛者答对的题数为则不答的题数为题，
根据题意得，，
解得，
则，
所以他答对了题，不答题．
（3）参赛者的得分不可能为奇数．
设参赛者答对了道题，则答错了道，
所以他的得分为：，
因和为非负整数，
所以为偶数，
所以为偶数．
因此参赛者的得分不可能为奇数．
25. 阅读理解：
如图，从的顶点出发，在的内部作一条射线，将分得的两个角为和，其中至少有一个角与互为补角，则称该射线为的“分补线”．请回答以下问题：
（1）若，，请判断此时是否为的“分补线”，并说明理由；
（2）若平分，为的“分补线”，
①当与重合时，求的度数；
②当为的“分补线”时，请画出图形并求出此时的度数．
解：（1）是的“分补线，理由如下：
∵，，，
∴，
∴，
∴是的“分补线；
（2）①当与重合时，
∵平分，
∴，
∵为的“分补线”，
∴，
∴，
②设
∵平分，为的“分补线”，
∴，
∴
又∵为的“分补线”，则在的内部，
如图所示，
当
∴
∵
∴
即
解得：
∵为的“分补线”，
当，
∴
∵
∴
解得：
综上所述，或参赛者
答对题数
答错题数
不答题数
得分