专题03 三次函数的图像与性质（4大题型）-2025年高考数学二轮热点题型归纳与变式演练（新高考通用）

这是一份专题03 三次函数的图像与性质（4大题型）-2025年高考数学二轮热点题型归纳与变式演练（新高考通用），文件包含专题03三次函数的图像与性质4大题型-2025年高考数学二轮热点题型归纳与变式演练新高考通用原卷版docx、专题03三次函数的图像与性质4大题型-2025年高考数学二轮热点题型归纳与变式演练新高考通用解析版docx等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。

目录（Ctrl并单击鼠标可跟踪链接）
TOC \ "1-1" \h \u \l "_Tc7162" 题型01 三次函数的零点 PAGEREF _Tc7162 \h 1
\l "_Tc5372" 题型02 三次函数的极值、极值点 PAGEREF _Tc5372 \h 2
\l "_Tc8327" 题型03 三次函数的切线 PAGEREF _Tc8327 \h 4
\l "_Tc22436" 题型04 三次函数的对称性 PAGEREF _Tc22436 \h 5
题型01 三次函数的零点
【解题规律·提分快招】
【典例训练】
一、单选题
1．（24-25高三上·辽宁·期中）已知函数的三个零点分别为，，，若函数满足，则的取值范围为（ ）
A．B．C．D．
二、多选题
2．（24-25高三上·辽宁沈阳·期中）已知函数，则（ ）
A．B．若，则的极大值点为
C．若至少有两个零点，则D．在区间上单调递增
3．（24-25高三上·甘肃兰州·阶段练习）已知三次函数有三个不同的零点，函数也有三个零点，则（ ）
A．
B．若成等差数列，则
C．
D．
三、填空题
4．（24-25高三上·广东·阶段练习）已知若函数有两个零点，则的取值范围为
5．（0分）（24-25高三上·天津·阶段练习）已知函数，若方程有且仅有两不等实根，则实数的取值范围是 .
题型02 三次函数的极值、极值点
【解题规律·提分快招】
【典例训练】
一、单选题
1．（2024·四川泸州·一模）已知函数在处取得极大值，则的值是（ ）
A．1B．2C．3D．4
2．（24-25高三上·吉林长春·阶段练习）若是函数的极小值点，则的极大值为（ ）
A．B．C．D．
3．（24-25高三上·辽宁·阶段练习）已知函数，是的导函数，则下列说法错误的是（ ）
A．“”是“为奇函数”的充要条件
B．“”是“为增函数”的充要条件
C．若不等式的解集为且，则的极小值为
D．若、是方程的两个不同的根，且，则或
二、多选题
4．（24-25高三上·江西南昌·阶段练习）已知函数，2为的极大值点，则下列结论正确的有（ ）
A．
B．若4为函数的极小值点，则
C．若在内有最小值，则的取值范围是
D．若有三个互不相等的实数解，则的取值范围是
5．（24-25高三上·江苏·阶段练习）已知三次函数，则（ ）
A．函数一定有两个极值点B．当时，
C．当时，的极小值为0D．在区间上的值域为
三、填空题
6．（0分）（24-25高三上·四川攀枝花·阶段练习）已知函数两个极值点分别为椭圆与双曲线的离心率，则实数的取值范围是 .
题型03 三次函数的切线
【典例训练】
一、单选题
1．（23-24高三上·广东汕头·阶段练习）若过点可作曲线三条切线，则（ ）
A．B．
C．或D．
二、多选题
2．（24-25高三上·河北张家口·开学考试）已知函数，则（ ）
A．时，是的极大值点
B．若存在三个零点，则
C．当时，过点可以作的切线，有且只有一条
D．存在，使得
3．（24-25高三上·广东广州·阶段练习）已知函数，则（ ）
A．时，若有3个零点，则实数的取值范围是
B．时，过可作函数的切线有两条
C．若直线与曲线有3个不同的交点，，，且，则
D．若存在极值点，且，其中，则
4．（24-25高三上·浙江·开学考试）三次函数叙述正确的是（ ）
A．函数可能只有一个极值点
B．当时，函数的图象关于点中心对称
C．当时，过点的切线可能有一条或者两条
D．当时，在点处的切线与函数的图象有且仅有两个交点
三、填空题
5．（23-24高三上·四川内江·期末）已知函数，若过点可作曲线的三条切线，则的取值范围是 ．
题型04 三次函数的对称性
【解题规律·提分快招】
【典例训练】
一、多选题
1．（2024高三·全国·专题练习）（多选）已知函数，则（ ）
A．有两个极值点B．有三个零点
C．点是曲线的对称中心D．直线是曲线的切线
2．（24-25高三上·辽宁丹东·期中）设函数，则（ ）
A．有三个零点B．是的极小值点
C．的图象关于点对称D．当时，
3．（24-25高三上·陕西汉中·阶段练习）设，函数，则下列说法正确的有（ ）
A．当时，函数为增函数B．点为函数图象的对称中心
C．存在a，使得函数有且仅有一个极值点D．函数至少有一个零点
4．（24-25高三上·广西南宁·阶段练习）函数，则下列结论正确的是（ ）
A．当时，函数只有一个零点
B．若函数的对称中心为，则
C．若函数在上为减函数，则
D．当时，设的三个零点分别为，，曲线在点，，处的切线斜率分别记为，，，则
二、解答题
5．（24-25高三上·辽宁·阶段练习）设函数，其中是常数．
(1)讨论的单调性；
(2)若是函数的极值点，证明：函数的图象关于点成中心对称．
一、单选题
1．（24-25高三上·福建龙岩·期中）已知函数，若对任意，都有，则实数的取值范围是（ ）
A．B．C．D．
2．（24-25高三上·四川·期中）已知实数a满足，则函数的零点个数为（ ）
A．0B．1C．2D．3
3．（24-25高三上·湖南·阶段练习）已知函数，若的图象上存在两点，，使得的图象在，处的切线互相垂直，且过点只能作1条切线与的图象相切，则的取值范围是（ ）
A．B．
C．D．
二、多选题
4．（24-25高三上·云南昆明·阶段练习）已知函数y=fx的导函数为y=gx，且，则（ ）
A．点是曲线y=gx的对称中心B．函数有三个零点
C．函数只有一个极值点D．当时，
5．（24-25高三上·湖南·阶段练习）已知函数，则（ ）
A．的值域为
B．图象的对称中心为
C．当时，在区间内单调递减
D．当时，有两个极值点
6．（24-25高三上·广西·期中）已知函数，则（ ）
A．若，则有三个零点B．若，则函数存在个极值点
C．在单调递减，则D．若在恒成立，则
7．（24-25高三上·江西·阶段练习）已知函数，下列结论正确的是（ ）
A．若是的极小值点，则在上单调递减
B．若是的极大值点，则且
C．若，且的极小值大于0，则的取值范围为
D．若，且在上的值域为，则的取值范围为
8．（24-25高三上·海南省直辖县级单位·开学考试）已知函数，其中实数，则下列结论正确的是（ ）
A．在上单调递增
B．当有且仅有3个零点时，的取值范围是
C．若直线与曲线有3个不同的交点，且，则
D．当时，过点可以作曲线的3条切线
9．（24-25高三上·江西·阶段练习）若存在实数b使得方程有四个不等的实根，则mn的值可能为（ ）
A．B．2025C．0D．
10．（24-25高三上·江西赣州·阶段练习）若函数有三个零点，则下列说法中正确的是（ ）
A．
B．
C．若成等差数列，则
D．若成等比数列，则
三、解答题
11．（24-25高三上·山东济宁·阶段练习）已知函数.
(1)试确定函数的极大值与1的大小关系，并说明理由；
(2)若函数有3个零点，求实数的取值范围.
一、三次函数概念
定义：形如fx=ax3+bx2+cx+da≠0叫做三次函数
f'x=3ax2+2bx+c，把Δ=4b2−12ac叫做三次函数导函数的判别式
当Δ>0时，令f'x=0，记两根为x1=−b−b2−3ac3a，x2=−b+b2−3ac3a
二、三次函数的零点个数
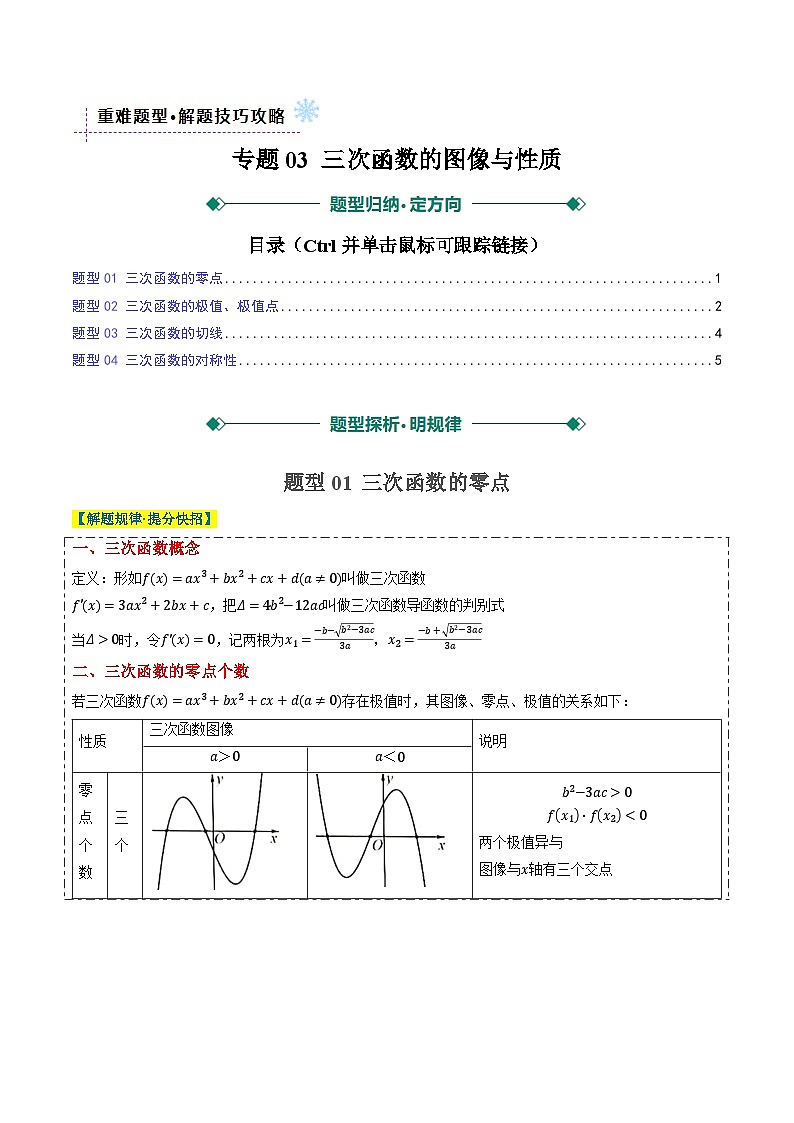
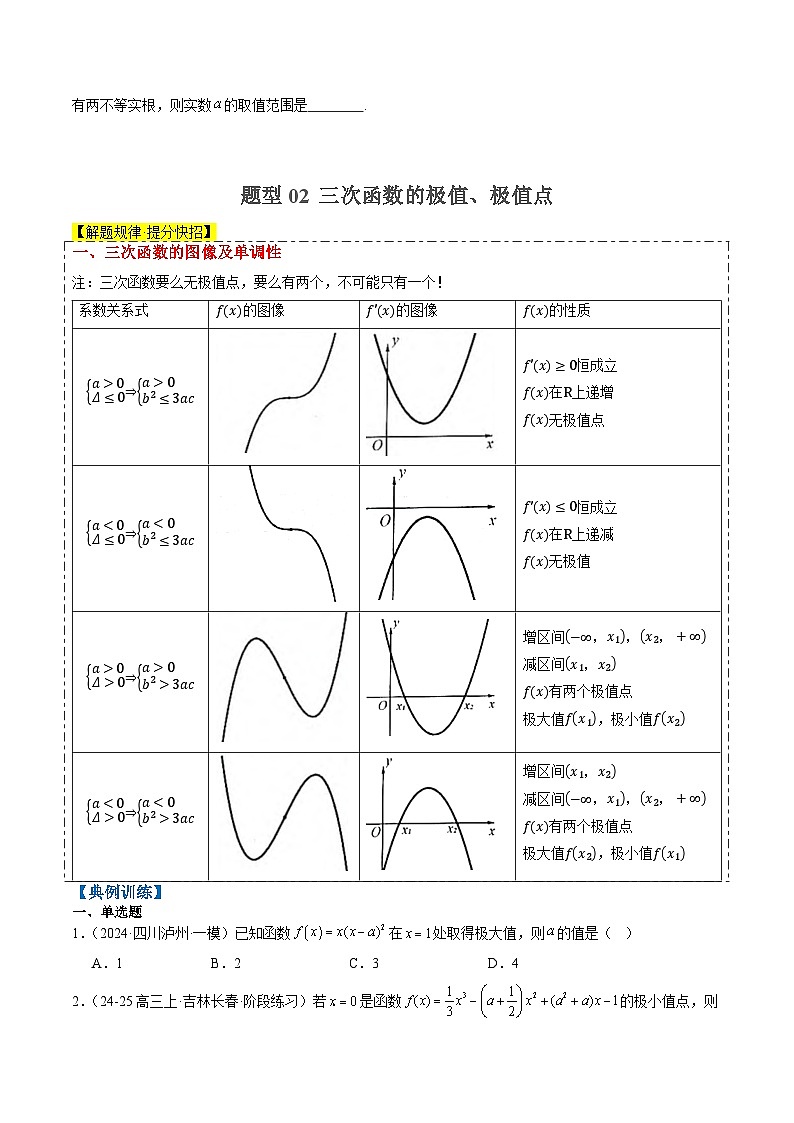
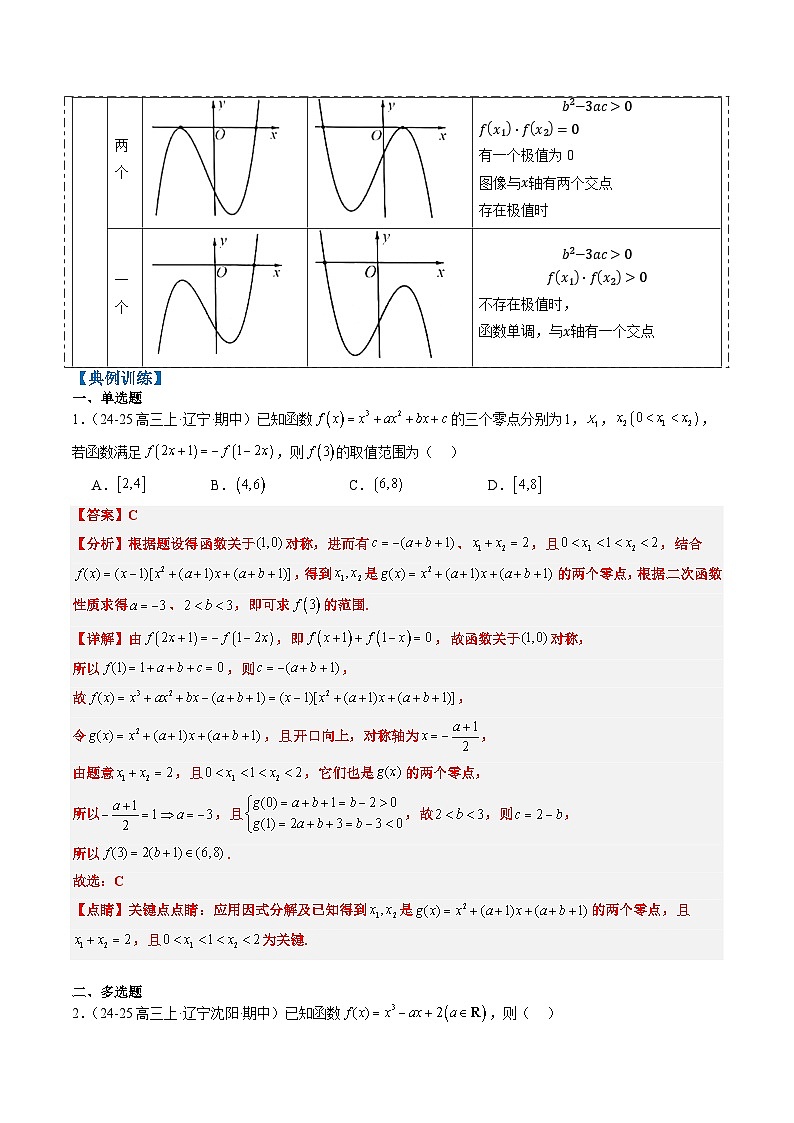
若三次函数fx=ax3+bx2+cx+da≠0存在极值时，其图像、零点、极值的关系如下：
性质
三次函数图像
说明
a＞0
a＜0
零点个数
三个
b2−3ac>0
fx1⋅fx20
fx1⋅fx2=0
有一个极值为0
图像与x轴有两个交点
存在极值时
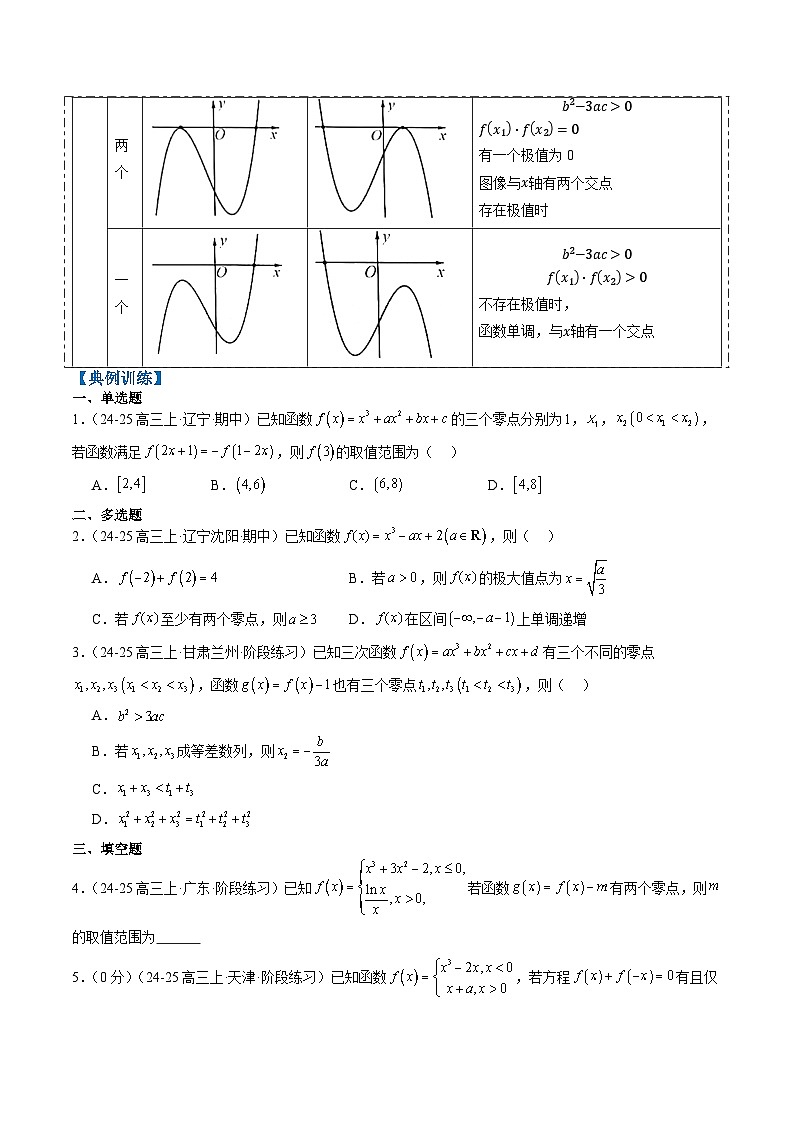
一个
b2−3ac>0
fx1⋅fx2>0
不存在极值时，
函数单调，与x轴有一个交点
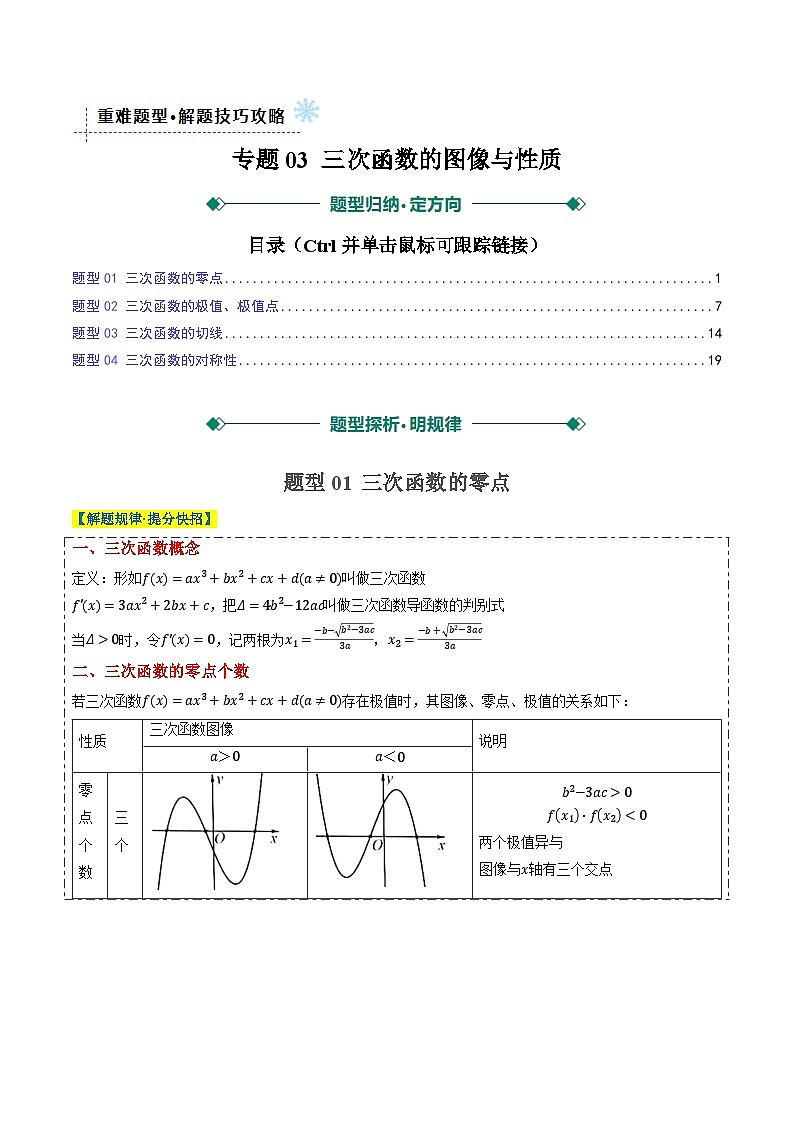
一、三次函数的图像及单调性
注：三次函数要么无极值点，要么有两个，不可能只有一个！
系数关系式
fx的图像
f'x的图像
fx的性质
a>0Δ≤0⇒a>0b2≤3ac
f'x≥0恒成立
fx在R上递增
fx无极值点
a