
2024-2025学年广东省中山市高一上册第二次月考数学检测试题
展开
这是一份2024-2025学年广东省中山市高一上册第二次月考数学检测试题,共5页。试卷主要包含了 若, 函数的单调递增区间是, 函数的部分图象大致是, 设,,,则, 图中阴影部分所表示的集合是等内容,欢迎下载使用。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
一、单选题(本题共8小题,每小题5分,每小题只有一个正确答案)
1. 将化成分数指数幂的形式是( )
A. B. C. D.
2. 已知函数,则下列结论正确的是( )
A. 偶函数,递减区间是B. 是偶函数,递增区间是
C. 是奇函数,递减区间是D. 是奇函数,递减区间是
3. 若:“”,:“”,则是的( )
A. 充要条件B. 必要不充分条件
C. 充分不必要条件D. 既不充分也不必要条件
4. 函数的单调递增区间是( )
A. B. C. D.
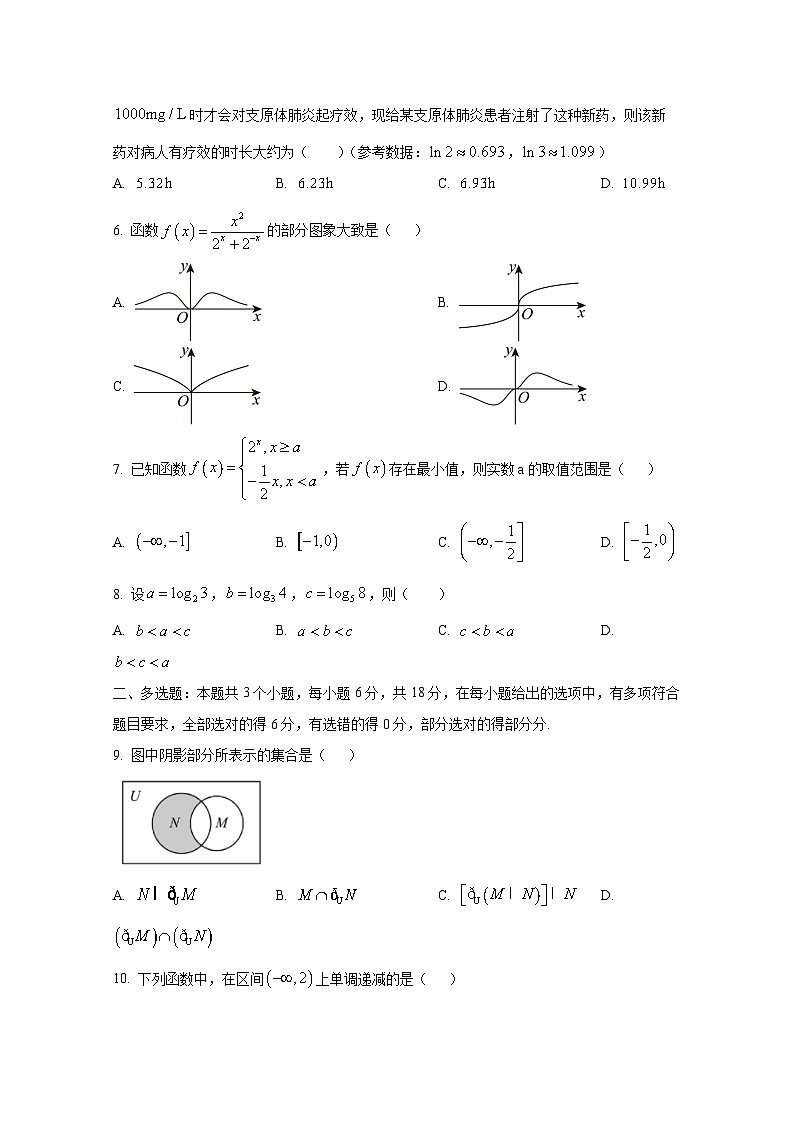
5. 我国某科研机构新研制了一种治疗支原体肺炎的注射性新药,并已进入二期临床试验阶段.已知这种新药在注射停止后的血药含量(单位:)随着时间(单位:)的变化用指数模型描述,假定该药物的消除速率常数(单位:),刚注射这种新药后的初始血药含量,且这种新药在病人体内的血药含量不低于时才会对支原体肺炎起疗效,现给某支原体肺炎患者注射了这种新药,则该新药对病人有疗效的时长大约为( )(参考数据:,)
A. B. C. D.
6. 函数的部分图象大致是( )
A. B.
C. D.
7. 已知函数,若存在最小值,则实数a的取值范围是( )
A. B. C. D.
8. 设,,,则( )
A. B. C. D.
二、多选题:本题共3个小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,有选错的得0分,部分选对的得部分分.
9. 图中阴影部分所表示的集合是( )
A. B. C. D.
10. 下列函数中,在区间上单调递减的是( )
A B.
C. D.
11. 已知关于不等式的解集为,则( )
A. B. C. D.
三、填空题(每小题5分,共15分)
12 ________.
13. 已知幂函数的图象关于y轴对称,且在上单调递减,实数a满足,则实数a的取值范围是________.
14. 在数学中连乘符号是“Π”,例如:若,则,已知函数,,,且,则使为整数的共有__________个.
四、解答题(本大题共5小题)
15. 已知集合,集合.
(1)当时,求;
(2)若,求实数a取值范围.
16. 已知函数.
(1)若不等式的解集为,求实数的取值范围;
(2)当时,若在区间0,2上的最小值为,求的值;
(3)当时,若函数在区间上的图象始终在的图象的下方,求实数的取值范围.
17. 为了缓解交通压力,需要限定汽车速度,交管部门对某路段作了调研,得到了某时间段内的车流量(千辆/小时)和汽车平均速度(千米/小时)的下列数据:
为了描述车流量和汽车平均速度的关系,现有以下三种模型供选择:,,
(1)选出你认为最符合实际的函数模型,请说明理由并计算的值;
(2)计算该路段最大车流量及最大车流量时汽车的平均速度.
18. 已知定义域为的函数是奇函数.
(1)求b的值;
(2)判断函数在上的单调性,并证明你的结论;
(3)若,使成立,求实数k的取值范围.
19. 设A,B是非空实数集,如果对于集合A中的任意两个实数x,y,按照某种确定的关系f,在B中都有唯一确定的数z和它对应,那么就称f:为从集合A到集合B的一个二元函数,记作,,其中A称为二元函数f的定义域.
(1)已知,若,,,求;
(2)设二元函数f的定义域为I,如果存在实数M满足:①,都有,②,使得.那么,我们称M是二元函数的下确界.若,且,判断函数是否存在下确界,若存在,求出此函数的下确界,若不存在,说明理由.
(3)的定义域为,若,对于,都有,则称f在D上是关于h单调递增.已知在上是关于1单调递增,求实数的取值范围.
10
30
40
60
70
0.8
6
8
4.8
3.5
相关试卷
这是一份2024-2025学年广东省兴宁市高一上册第二次月考数学检测试题,共4页。试卷主要包含了 函数的部分图象大致为, 设,,,则等内容,欢迎下载使用。
这是一份2024-2025学年广东省深圳市高一上册第二次月考数学检测试题,共4页。
这是一份2024-2025学年广东省兴宁市高一上学期第二次月考 数学质量检测试题(含答案),共11页。









