2025年九年级中考数学二轮复习难点题型突破课件：费马点模型

这是一份2025年九年级中考数学二轮复习难点题型突破课件：费马点模型，共13页。PPT课件主要包含了由图可知AP＝DF，连接PGCM等内容，欢迎下载使用。
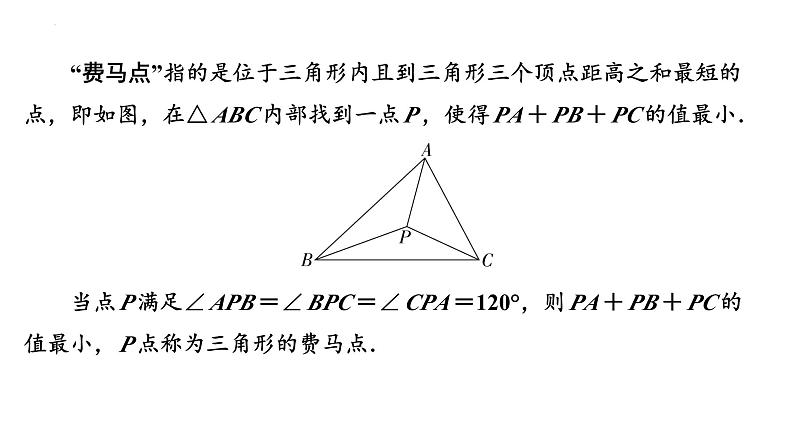
“费马点”指的是位于三角形内且到三角形三个顶点距高之和最短的 点，即如图，在△ABC内部找到一点P，使得PA＋PB＋PC的值最小．
当点P满足∠APB＝∠BPC＝∠CPA＝120°，则PA＋PB＋PC的 值最小，P点称为三角形的费马点．
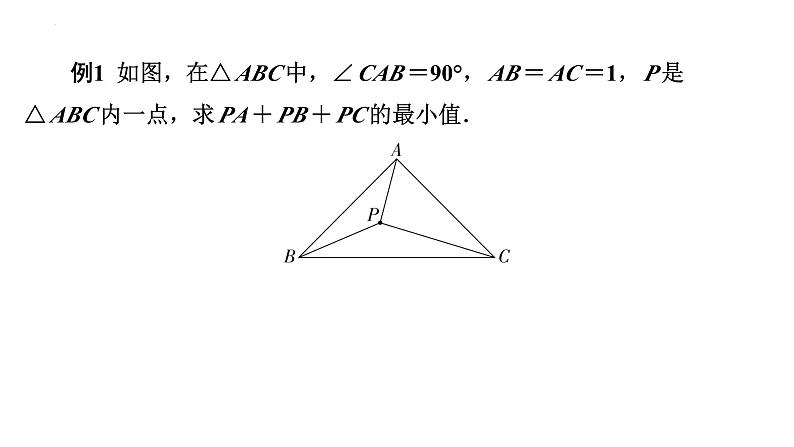
例1 如图，在△ABC中，∠CAB＝90°，AB＝AC＝1，P是 △ABC内一点，求PA＋PB＋PC的最小值．
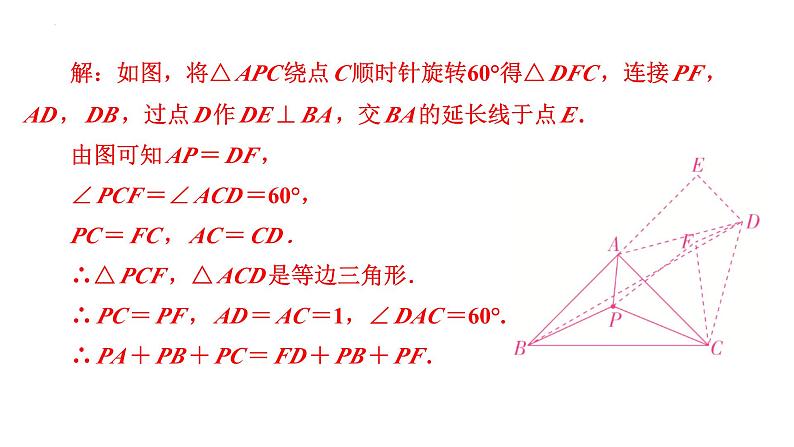
解：如图，将△APC绕点C顺时针旋转60°得△DFC，连接PF， AD，DB，过点D作DE⊥BA，交BA的延长线于点E.
∠PCF＝∠ACD＝60°，
PC＝FC，AC＝CD．
∴△PCF，△ACD是等边三角形．
∴PC＝PF，AD＝AC＝1，∠DAC＝60°.
∴PA＋PB＋PC＝FD＋PB＋PF.
∴当B，P，F，D四点共线时，PA＋PB＋PC的值最小，最小值为BD的长．
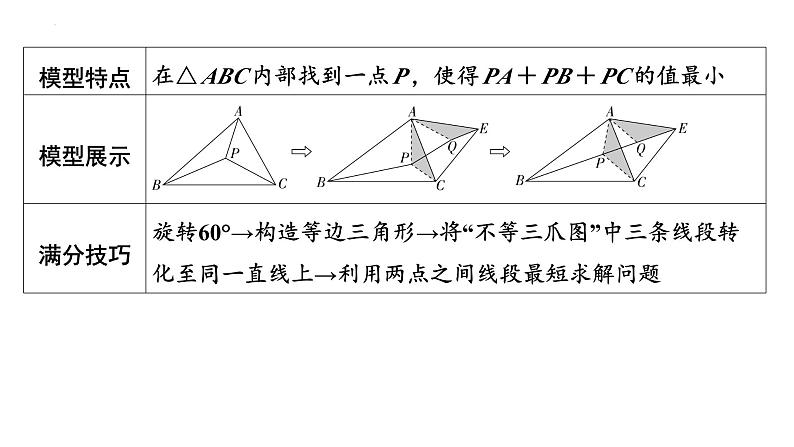
解：如图，将△ABP绕点A顺时针旋转60°得到△AMG.
∵AG＝AP，∠GAP＝60°，
∴△GAP是等边三角形．∴PA＝PG.
∵GM＝BP，∴AP＋BP＋CP＝PG＋GM＋CP.
∴当M，G，P，C共线时，AP＋BP＋CP的值最小，最小值为线 段CM的长．
∵∠BAM＝60°，∠BAC＝30°，∴∠MAC＝90°.∴AM＝AC＝2.
1． 如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一 点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为 ⁠ ⁠．
2． 如图，四边形ABCD是菱形，AB＝6，且∠ABC＝60°，M是 菱形内任一点，连接AM，BM，CM，则AM＋BM＋CM的最小值 为 ⁠．