2025年河南省九年级中考数学一轮复习课件专项练习相似三角形判定的模型

这是一份2025年河南省九年级中考数学一轮复习课件专项练习相似三角形判定的模型，共46页。
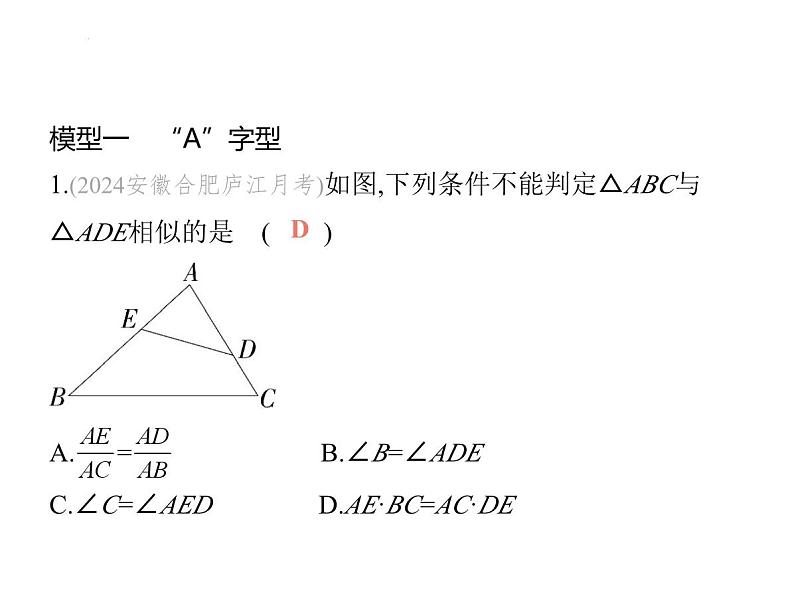
1.(2024安徽合肥庐江月考)如图,下列条件不能判定△ABC与 △ADE相似的是 (　　) A. = 　　　     B.∠B=∠ADEC.∠C=∠AED　　　    D.AE·BC=AC·DE
解析　由题图知∠EAD=∠BAC.A.符合两边夹角定理,故A能 判定△ABC与△ADE相似;B.符合两角定理,故B能判定△ABC 与△ADE相似;C.符合两角定理,故C能判定△ABC与△ADE 相似;D.由AE·BC=AC·DE,得 = ,不符合两边夹角定理,故D不能判定△ABC与△ADE相似.故选D.
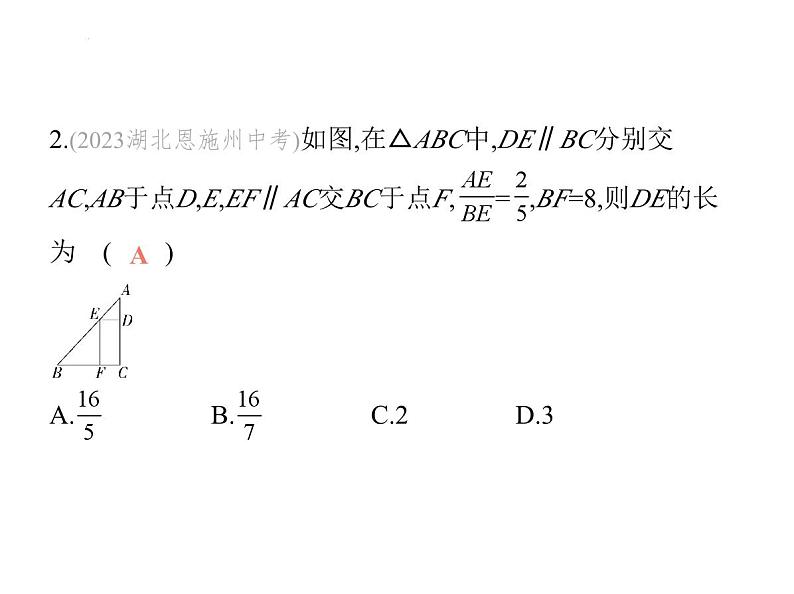
2.(2023湖北恩施州中考)如图,在△ABC中,DE∥BC分别交 AC,AB于点D,E,EF∥AC交BC于点F, = ,BF=8,则DE的长为 (　　) A. 　　　    B. 　　　    C.2　　　    D.3
解析　∵DE∥BC,EF∥AC,∴四边形EFCD是平行四边形, ∴DE=CF,设DE=CF=x,∵BF=8,∴BC=BF+CF=8+x,∵DE∥BC, ∴△AED∽△ABC,∴ = ,∵ = ,∴ = ,∴ = ,即 = ,解得x= ,即DE的长为 .故选A.
3.(方程思想)(2024江苏连云港灌南二模)如图,在△ABC中, BD平分∠ABC,DE∥BC交AB于点E,若AB=6,BC=4,则DE=    　    . 
解析　∵BD平分∠ABC,∴∠EBD=∠CBD.∵DE∥BC,∴∠EDB =∠CBD,∴∠EBD=∠EDB,∴DE=BE.设DE=BE=x,∵AB =6,∴AE=6-x.∵DE∥BC,∴△ADE∽△ACB,∴ = ,即 = ,解得x= ,即DE= .
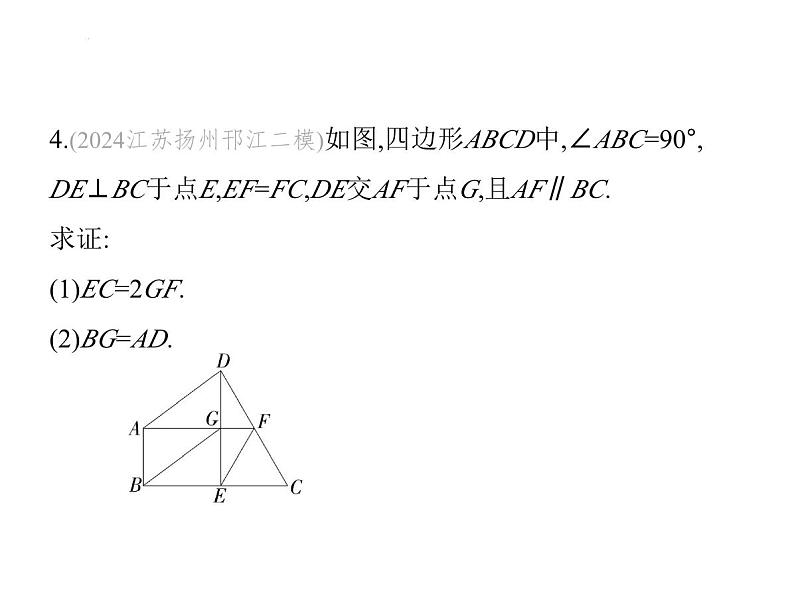
4.(2024江苏扬州邗江二模)如图,四边形ABCD中,∠ABC=90°,DE⊥BC于点E,EF=FC,DE交AF于点G,且AF∥BC.求证:(1)EC=2GF.(2)BG=AD. 
证明　(1)∵DE⊥BC于点E,∴∠CED=90°,∴∠FED+∠FEC =90°,∠FDE+∠C=90°,∵EF=FC,∴∠FEC=∠C,∴∠FED= ∠FDE,∴EF=FD,∴FD=FC= CD,∵AF∥BC,∴GF∥EC,∴△DGF∽△DEC,∴ = = ,∴EC=2GF.(2)∵∠CED=∠ABC=90°,∴GE∥AB,∵AG∥BE,∴四边形 ABEG是平行四边形,∴AB=GE,∵GF∥EC,∴ = =1,∴GD=GE,∴GD=AB,∵GD∥AB,∴四边形ABGD是平行四边 形,∴BG=AD.
5.(2023陕西中考)如图,DE是△ABC 的中位线,点F在DB上, DF=2BF,连接EF并延长,与CB的延长线相交于点M.若BC=6, 则线段CM的长为(　　) A. 　　　    B.7　　　    C. 　　　    D.8
解析　∵DE是△ABC的中位线,∴DE∥BC,DE= BC= ×6=3,∴△DEF∽△BMF,∴ = = =2,∴BM= ,∴CM=BC+BM= .故选C.
6.(2024江苏无锡一模)如图,矩形ABCD为☉O的内接四边形, AB=2,BC=3,E为BC上一点,且BE=1,延长AE交☉O于点F,则线 段AF的长为　　　    . 
解析　如图,连接CF,∵四边形ABCD是矩形,∴∠ABC=90°, ∴AE= = = .∵BC=3,BE=1,∴CE=2.∵∠ABC与∠CFA都为 所对的圆周角,∴∠ABE=∠CFE.∵∠AEB=∠CEF,∴△ABE∽△CFE,∴ = ,∴FE= = = .∴AF=AE+FE=   . 
7.(2024黑龙江大庆肇源期中)如图,在▱ABCD中,E为边BC上 一点,连接AE并延长交DC的延长线于点M,交BD于点G,过点 G作GF∥AD交DC于点F, = .(1)若BD=20,求BG的长.(2)求 的值.
解析　(1)∵GF∥AD,AD∥BC,∴GF∥BC,∴ = = ,∴ = = ,∵BD=20,∴BG=20× =8.(2)∵BC∥AD,∴△BEG∽△DAG,∴ = = ,∵AD=BC,∴ = =1- = ,∵AD∥BC,∴△ECM∽△ADM,∴ = = .
8.(2023上海徐汇模拟)如图所示,给出下列条件:①∠B=∠ACD; ②∠ADC=∠ACB;③ = ;④AC2=AD·AB.其中能够判定△ABC∽△ACD的个数为(　　) A.1　　　    B.2　　　    C.3　　　    D.4
解析　①∵∠B=∠ACD,∠DAC=∠BAC,∴△ABC∽△ACD, 故①符合题意;②∵∠ADC=∠ACB,∠DAC=∠BAC,∴△ABC ∽△ACD,故②符合题意;③ = ,但∠ACD和∠ABC不一定相等,因此不能判定△ABC∽△ACD,故③不符合题 意;④∵AC2=AD·AB,∴ = ,又∵∠DAC=∠BAC,∴△ABC∽△ACD,故④符合题意.综上所述,能够判定△ABC∽△ACD 的条件的个数为3.故选C.
9.(2024山东济南济阳期末)如图,在△ABC中,点D是AB边上 一点,连接CD.已知AD=4,BD=5,AC=6,CD=3,那么线段BC的 长度是　　　    . 
解析　∵AD=4,BD=5,AC=6,∴ = = , = = ,∴ = ,∵∠CAD=∠BAC,∴△ABC∽△ACD,∴ = ,∵CD=3,∴BC= .
10.(2024云南红河州二模)如图,AB是☉O的直径,点C在☉O 上,延长BA至点D,使CD2=AD·BD.(1)求证:CD是☉O的切线.(2)若☉O的半径为 ,BC=4,求 的值. 
解析　(1)证明:连接OC.∵AB是☉O的直径,∴∠ACB=90°,即∠BAC+∠B=90°.
∵CD2=AD·BD,∴ = .又∵∠ADC=∠CDB,∴△ADC∽△CDB,∴∠ACD=∠B,∵OA=OC,∴∠BAC=∠OCA.∴∠OCA+∠ACD=90°,即∠OCD=90°.∴OC⊥CD.∵OC是☉O的半径,∴CD是☉O的切线.(2)由题可知AB=2 .在Rt△ABC中,∠ACB=90°,AC= =2.
由(1)知△ADC∽△CDB,OC⊥CD,∴ = = = = .设AD=x,则CD=2x,在Rt△OCD中,OC2+CD2=OD2,即( )2+(2x)2=( +x)2,解得x1= ,x2=0(舍去),∴CD= ,∴ = .
11.(2024浙江杭州西湖期中)如图,在矩形ABCD中,BD=2 .对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E, AE=3CE.则DE2的值为 (　　) A.4　　　    B.2 　　　    C. 　　　    D.4 
解析　∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=2 ,∵AE=3CE,∴AE= AC=  ,CE= AC= .由射影定理相似模型可得△ADE∽△DCE,∴ = ,∴DE2=AE·CE=  × = .故选C.
12.(2024北京石景山期中)如图,在Rt△ABC中,∠BAC=90°, AD⊥BC于点D,AB=3,BC=5,则BD=　　　    . 
13.(2024黑龙江大庆肇源期中)如图,CE是Rt△ABC的斜边AB 上的高,BG⊥AP.求证:CE2=ED·EP. 
证明　∵CE是Rt△ABC的斜边AB上的高,∴△ACE∽△CBE,∴ = ,即CE2=AE·BE.∵CE是Rt△ABC的斜边AB上的高,BG⊥AP,∴∠P+∠PAE=90°,∠DBE+∠PAE=90°,∴∠P=∠DBE,又∵∠AEP=∠DEB=90°,∴△AEP∽△DEB,∴ = ,即AE·BE=ED·EP,又∵CE2=AE·BE,∴CE2=ED·EP.
模型五　一线三等角模型
模型解读一线三等角模型:有三个等角的顶点在同一条直线上的基本 几何图形.如图,在△ABC中,D、E、F分别在AB、BC、AC 上,且∠DEF=∠B=∠C,则△BDE∽△CEF. 
14.(方程思想)(2022四川达州中考)如图,点E在矩形ABCD的 AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处, 若CD=3BF,BE=4,则AD的长为(　　) A.9　　　    B.12　　　    C.15　　　    D.18
解析　∵四边形ABCD是矩形,∴AD=BC,∠A=∠B=∠C=90°. 由翻折可得AD=DF=BC,∠A=∠DFE=90°,∴∠BFE+∠DFC =∠BFE+∠BEF=90°,∴∠BEF=∠CFD,∴△BEF∽△CFD, ∴ = ,∵CD=3BF,∴CF=3BE=12,设BF=x,则CD=3x,DF=BC=x+12,∵∠C=90°,∴Rt△CDF中,CD2+CF2=DF2,∴(3x)2+ 122=(x+12)2,解得x=3(舍去x=0),∴AD=DF=3+12=15.故选C.
15.(新独家原创)如图,等边三角形ABC的边长为6,点D,E分别 是BC,AC上的点,将△ABC沿DE折叠,使点C落在边AB上的C' 处,若点C'是线段AB的三等分点,则线段BD的长为　　　    . 
解析　∵等边三角形ABC的边长为6,∴AB=BC=AC=6,∠A= ∠B=∠C=60°,∴∠AC'E+∠AEC'=120°.由折叠的性质可知, ∠DC'E=∠C=60°,∴∠AC'E+∠BC'D=120°,∴∠BC'D= ∠AEC',∴△AEC'∽△BC'D,∴ = = .设BD=x,AE=y,则C'D=CD=6-x,C'E=CE=6-y,∵点C'是线段AB的三等分点, ∴分两种情况:当AC'=2时,BC'=4,则 = = ,解得x=2.5.当AC'=4时,BC'=2,则 = = ,解得x=3.2.综上,BD的长为2.5
16.(2024江苏苏州姑苏月考)如图,在△ABC中,AB=AC,点E在 边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F 分别在边AB,AC上.(1)求证: = .(2)当点E移动到BC的中点时,求证:FE平分∠DFC. 
证明　(1)∵AB=AC,∴∠B=∠C,∵∠BDE=180°-∠B-∠DEB, ∠CEF=180°-∠DEF-∠DEB,∠DEF=∠B,∴∠BDE=∠CEF, ∴△BDE∽△CEF.∴ = .(2)∵点E是BC的中点,∴BE=CE,∵ = ,∴ = ,∴  = ,又∠DEF=∠B=∠C,∴△DEF∽△ECF,∴∠DFE=∠CFE,∴FE平分∠DFC.
模型解读一对对应角顶点重合的两个相似三角形组成手拉手相似模 型,如图,△ADE∽△ABC,则△ABD∽△ACE.  
17.如图,△ABC和△BDE都是等边三角形,点D是AC上的点, 连接AE,下列结论正确的有(　　)①△BCD∽△BEO;②△AOD∽△EOB;③△AOE∽△DOB;④△BOD∽△BDA.
A.1个　　　    B.2个　　　    C.3个　　　    D.4个
解析　△ABC和△BDE都是等边三角形,且共顶点,由手拉手 相似模型可得△BCD∽△BAE,∴∠CBD=∠ABE,∠OAE= ∠DCB=60°,∵∠C=∠BEO=60°,∠CBD=∠ABE,∴△BCD∽ △BEO,故①正确;∵∠AOD=∠BOE,∠DAB=∠DEB=60°, ∴△AOD∽△EOB,故②正确;∵∠OAE=60°=∠BDE,∠AOE= ∠DOB,∴△AOE∽△DOB,故③正确;∵∠DBA=∠DBO,∠DAB =60°=∠ODB,∴△BOD∽△BDA,故④正确.所以,结论正确的 有4个.故选D.
18.(2023四川遂宁射洪一中期中)如图,在△ABC和△ADE中, ∠BAD=∠CAE,∠ABD=∠ACE.求证:(1)AB·AE=AC·AD.(2)△ABC∽△ADE. 
证明　(1)∵∠BAD=∠CAE,∠ABD=∠ACE,∴△ABD∽△ACE,∴ = ,∴AB·AE=AC·AD.(2)∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠DAC+∠CAE,即∠BAC=∠DAE,∵ = ,∴ = ,∴△ABC∽△ADE.
19.(新考法)(2024江苏连云港期中改编)如图,在Rt△ABC中, ∠ACB=90°,其中∠A=45°,AC=4,若点M是AC边上的动点,连 接BM,以BM为斜边作等腰直角△BMN,连接CN.(1)求证:AM= CN.(2)求△CMN面积的最大值. 
解析　(1)证明:在Rt△ABC中,∠ACB=90°,∠A=45°,∴△ABC 是等腰直角三角形,∴AB= BC,∠ABC=45°,∵△BMN是等腰直角三角形,∴BM= BN,∠MBN=45°=∠ABC,∴∠ABM=∠CBN,又∵ = = ,∴△ABM∽△CBN,∴ = ,即AM= CN.(2)如图,过点N作NH⊥AC,交AC的延长线于H,∵△ABM∽ △CBN,∴∠BCN=∠BAC=45°,∴∠ACN=135°,∴∠NCH=45°, ∴NH= CN= AM,∴△CMN面积= CM·NH= CM· (4-
CM)=- (CM-2)2+1,∴当CM=2时,△CMN面积取最大值1,∴△CMN面积的最大值为1.