专题四　全等与相似中的常见模型课件2025年中考数学一轮复习

这是一份专题四　全等与相似中的常见模型课件2025年中考数学一轮复习，共32页。PPT课件主要包含了典例精析，针对训练等内容，欢迎下载使用。
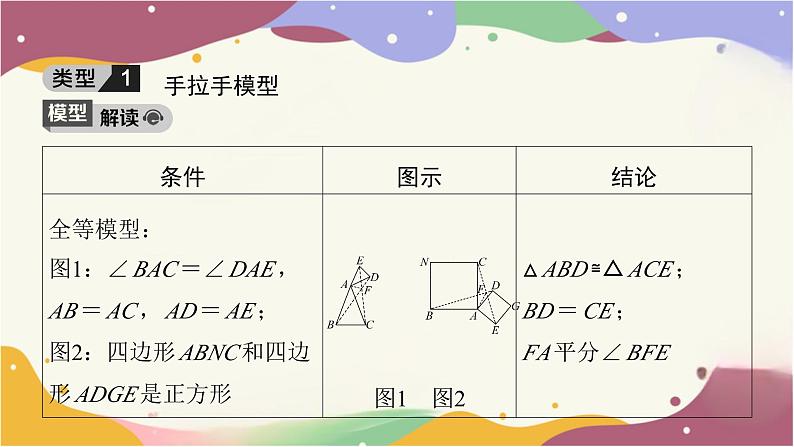
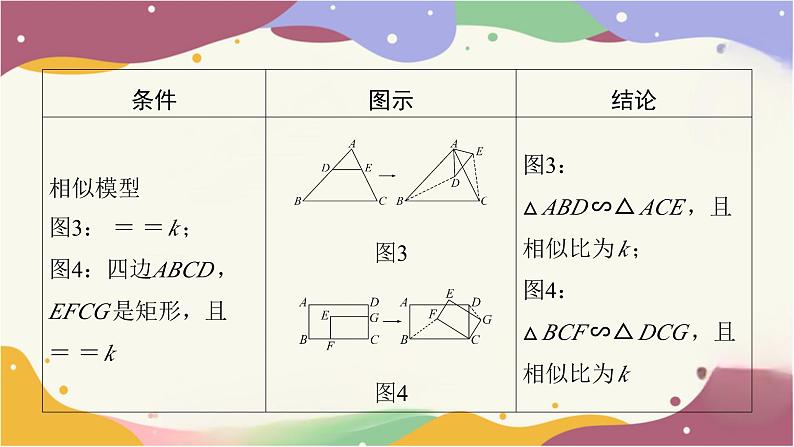
　手拉手模型
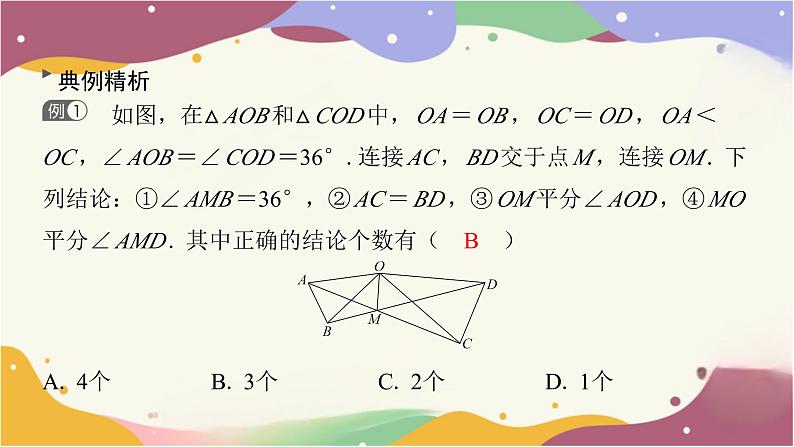
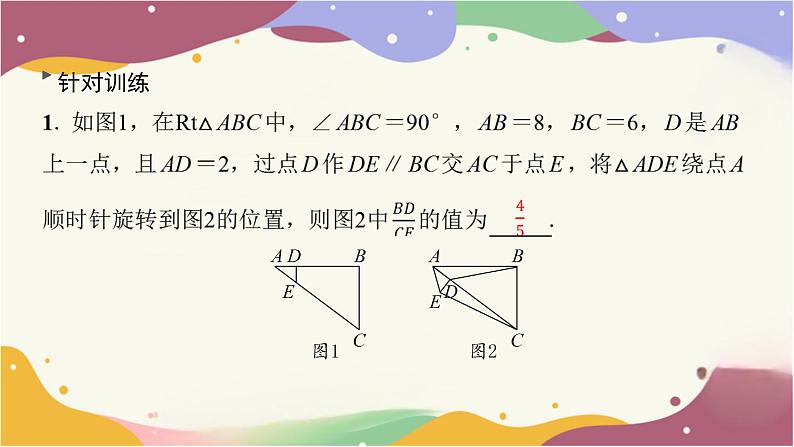
　如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜ OC，∠AOB＝∠COD＝36°.连接AC，BD交于点M，连接OM. 下 列结论：①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO 平分∠AMD. 其中正确的结论个数有（　B　）
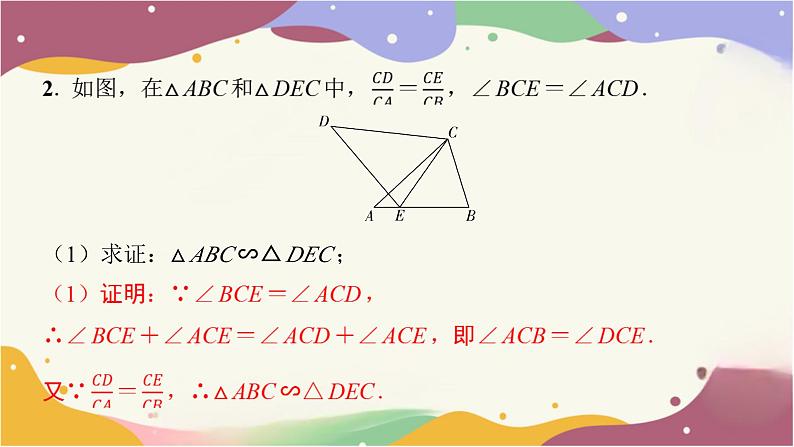
（1）求证：△ABC∽△DEC；
（2）若S△ABC∶S△DEC＝9∶16，BC＝6，求EC的长.
（1）求证：△CAD≌△CBE；
（2）若AD＝2，求CE的长；
（3）点D在AB边上运动时，试探究AD2＋BD2是否存在最小值，如果 存在，求出这个最小值；如果不存在，请说明理由.
　一线三等角模型
　如图，点A（0，3），B（1，0），将线段AB平移得到线段 DC，若∠ABC＝90°，BC＝2AB，则点D的坐标是（　D　）
【思路剖析】过点D作y轴的垂线构造一线三等角模型，得到相似三 角形，然后利用点A，B的坐标和相似三角形的判定与性质求得线段 的长，进而可得结论.
4. 如图，△ABC为等边三角形，点D，E分别在边BC，AB上， ∠ADE＝60°.若BD＝4DC，DE＝2.4，则AD的长为（　C　）
5. 如图，点E在矩形ABCD的AB边上，将△ADE沿DE翻折，点A恰 好落在BC边上的点F处，若CD＝3BF，BE＝4，则AD的长为 （　C　）
6. （2023重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点 D为BC上一点，连接AD. 过点B作BE⊥AD于点E，过点C作 CF⊥AD交AD的延长线于点F. 若BE＝4，CF＝1，则EF的长度 为 ⁠.
　半角模型
　如图，在正方形ABCD中，点E，F分别在BC，CD上，连接 AE，AF，EF，∠EAF＝45°.若∠BAE＝α，则∠FEC一定等于 （　A　）
【思路剖析】此题是典型的正方形半角模型，只需将△ADF绕点A顺 时针旋转90°得到全等三角形，根据全等三角形的性质可得∠AEF＝ ∠AEB，再根据∠FEC＝180°－∠AEF－∠AEB求解即可.
　对角互补模型
　如图，正方形ABCD的对角线AC，BD交于点O，E是AB上的 一点，连接OE，过点O作OF⊥OE交BC于点F，若AD＝2，则四边 形BFOE的面积为（　B　）
【思路剖析】利用全等三角形的性质把四边形BFOE的面积转化成 △BOC的面积即可得解.
9. 如图，△ABC是等边三角形，D是AC的中点，点E在BC的延长线 上，点F在AB上，∠EDF＝120°.
（1）求证：DE＝DF；
（1）证明：过点D作DM∥BC交AB于点M.
∵△ABC是等边三角形，∴AB＝BC＝AC，∠ACB＝∠ABC＝ 60°.∴∠DCE＝120°.
又∠EDF＝∠MDC＝120°，∴∠EDF－∠FDC＝∠MDC－ ∠FDC，即∠MDF＝∠CDE.