必修一模型课文ppt课件

这是一份必修一模型课文ppt课件，共60页。PPT课件主要包含了知识导航，典例精析，中考真题演练，模型一两定点一动点，模型二一定点两动点，模型三两定点两动点，模型四一定点两动点等内容，欢迎下载使用。
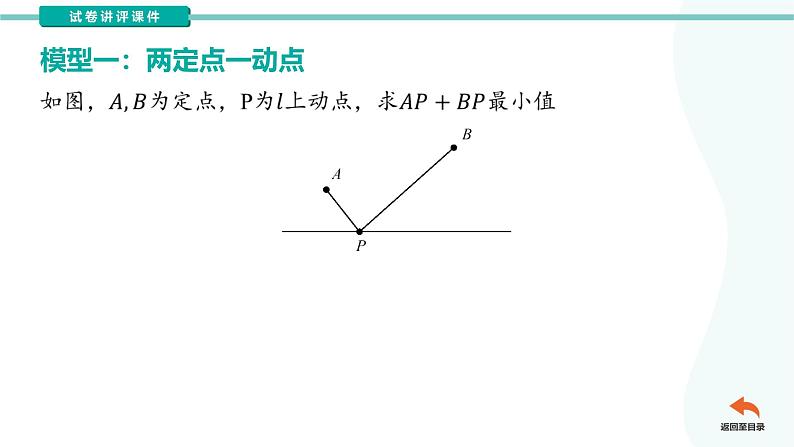
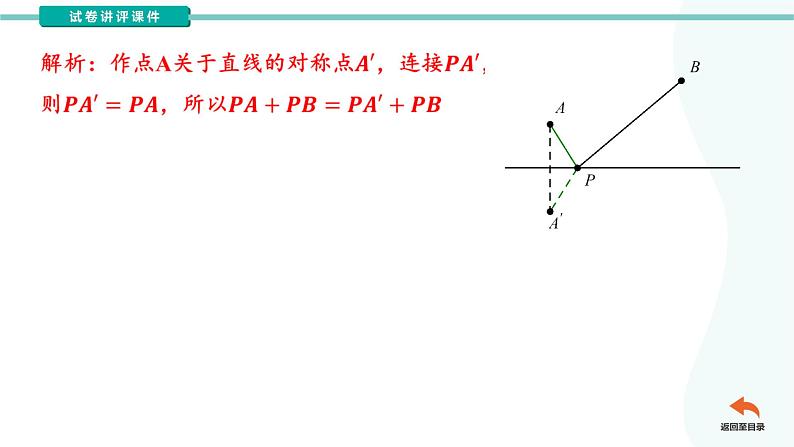
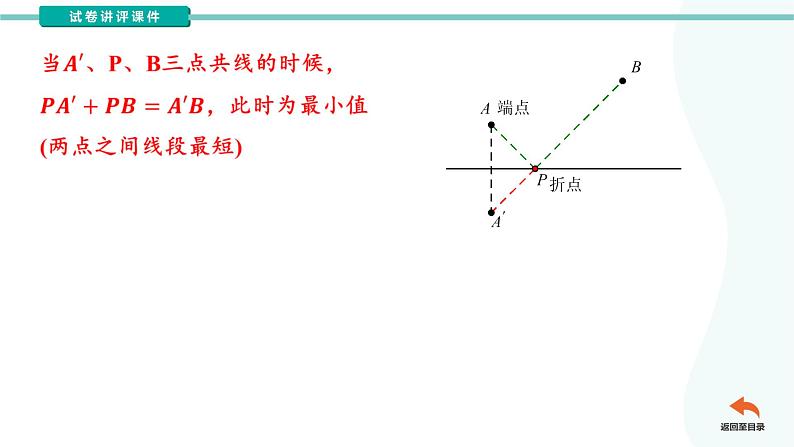
如图，P、Q为两定点，M、N分别为OA、OB上的动点，求四边形PQMN的最小值.
模型五：将军饮马有距离
(1)求抛物线的解析式和对称轴；
(1)求抛物线的解析式；
【分析】根据抛物线的对称性，进行求解即可；
(1)求点M的坐标及抛物线的解析式；
【点睛】本题考查求二次函数的解析式，二次函数的图象与性质，二次函数与几何变换综合，二次函数与相似三角形综合，最短路径问题，三角形面积公式等知识，难度较大，综合性大，作出辅助线和掌握转换思想是解题的关键，第二问的解题技巧是使用铅锤公式计算面积，第三问的技巧是转化成直角三角形的讨论问题，如果直接按相似讨论，则有四种情况，可以降低分类讨论的种类，第四问的技巧，是将点M向反方向移动，从而将两个动点转化成一个动点来解决.
(1)求二次函数的表达式；
(1)求该抛物线的表达式；
【分析】待定系数法求出函数解析式即可；
【点睛】本题是二次函数综合题，涉及最短路径问题，相似三角形问题，整体难度较大.
(3)点N为直线AB上的一点(点N不与点F重合)，在抛物线上是否存在一点M，使以点E、F、N、M为顶点的四边形为平行四边形？若存在，直接写出点M的坐标，若不存在，说明理由.
【点睛】本题主要考查了待定系数法求函数解析式，平行四边形存在性问题，解题过程中注意需要分类讨论.
【分析】分别求出点A、B坐标，即可求出AB的长度，将抛物线配成顶点式，即可确定点D坐标；
【答案】点P坐标为(-1，-2)；