中考数学考点针对训练历年真题手拉手模型课件

这是一份中考数学考点针对训练历年真题手拉手模型课件，共27页。PPT课件主要包含了CONTENTS，模型解读，模型归纳，模型应用，强化训练，AB∥CE，AC＝CD＋CE等内容，欢迎下载使用。
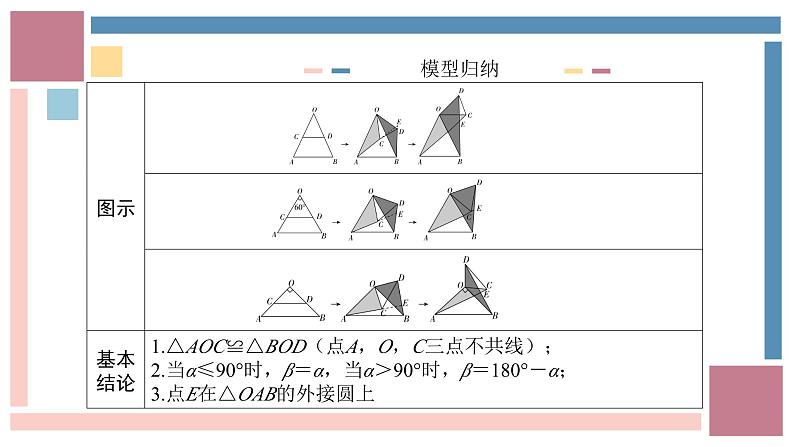
1.说明：两个三角形的顶点重合，其中一个三角形不动，另一个三角形绕着重合的顶点旋转，就好像手拉着手一样，所以称为“手拉手”模型.2.判断方法：将初始图形的公共顶点放在上方，图形正对着我们，左边顶点称为“左手”，右边顶点称为“右手”.
3.特点：（1）两条“拉手线”所在直线夹角与初始图形中公共顶点对应的角相等或互补；（2）三角形顺时针或逆时针旋转，得到的结论相同；（3）“手拉手”模型中，若“手拉手”的两个三角形均是等腰三角形，且公共顶点是顶角顶点，则对应边与“拉手线”组成的两个三角形全等；若两个三角形为非等腰三角形，则对应边与“拉手线”组成的两个三角形相似.
▶类型一　手拉手全等模型【例1】在学习全等三角形的知识时，数学兴趣小组发现这样一个模型：它是由共顶点且顶角相等的两个等腰三角形构成的，在相对位置变化时，始终存在着一对全等三角形.通过查询资料，他们得知这种模型称为“手拉手模型”，兴趣小组进行了如下操作：
（1）观察猜想：如图1，已知△ABC，△ADE均为等边三角形，点D在边BC上，且不与点B、C重合，连接易证△ABD≌△ACE，进而判断出AB与CE的位置关系是 　AB∥CE　⁠；
（2）类比探究：如图2，已知△ABC，△ADE均为等边三角形，连接CE，BD.若∠DEC＝60°，试说明B，D，E三点在同一条直线上；
（3）解决问题：如图3，已知点E在等边△ABC 的外部，并且与点B位于线段AC的异侧，连接AE，BE，CE.若∠BEC＝60°，AE＝3，CE＝2，请求出BE的长.
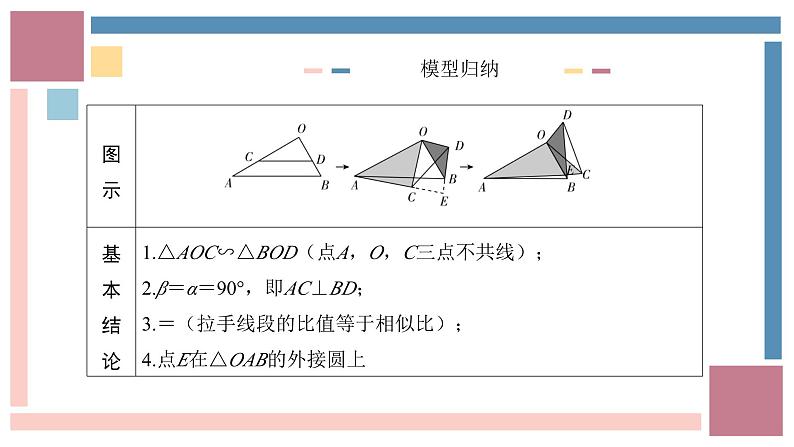
▶类型二　手拉手相似模型
【例2】如图1，已知△ABC和△ADE均为等腰直角三角形，点D，E分别在线段AB，AC上，∠C＝∠AED＝90°.
（2）类比探究：如图3，继续旋转△ADE，点F与点E不重合时，上述结论是否仍然成立，请说明理由.
▶类型一　手拉手全等模型1.如图1，在△ABC中，AB＝AC，∠BAC＝60°，D为BC边上一点（不与点B，C重合）.将线段AD绕点A逆时针旋转60°得到AE，连接EC，则：
（1）①∠ACE的度数是 　60°　⁠；②线段AC，CD，CE之间的数量关系是 　AC＝CD＋CE　⁠.
（2）如图2，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，请写出∠ACE的度数及线段AD，BD，CD之间的数量关系，并说明理由.
解：（2）∠ACE＝45°，BD2＋CD2＝2AD2.理由如下：由题意，得∠BAC＝∠DAE＝90°，∠B＝∠ACB＝45°，∴∠BAC－∠DAC＝∠DAE－∠DAC，即∠BAD＝∠CAE.
∴BD2＋CD2＝2AD2.
（3）如图3，在Rt△DBC中，DB＝3，DC＝5，∠BDC＝90°，若点A满足AB＝AC，∠BAC＝90°，请直接写出线段AD的长.
▶类型二　手拉手相似模型2.如图1，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，D，E分别是BC，AC的中点，连接DE，将△EDC绕点C按逆时针方向旋转，记旋转角为α.
②当△ACE为直角三角形时，直接写出线段BD的长.