微专题5 相似三角形常见模型课件2025年中考数学一轮复习

这是一份微专题5 相似三角形常见模型课件2025年中考数学一轮复习，共27页。PPT课件主要包含了－4t等内容，欢迎下载使用。
A字模型
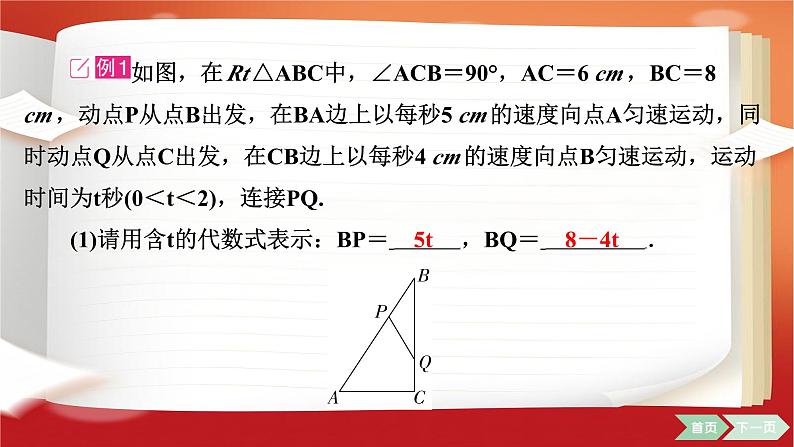
如图，在Rt△ABC中，∠ACB＝90°，AC＝6 cm，BC＝8 cm，动点P从点B出发，在BA边上以每秒5 cm的速度向点A匀速运动，同 时动点Q从点C出发，在CB边上以每秒4 cm的速度向点B匀速运动，运动 时间为t秒(0＜t＜2)，连接PQ.
(1)请用含t的代数式表示：BP＝ ，BQ＝ ⁠．
(2)当t为何值时，△BPQ与△ABC相似？
∵△BPQ与△ABC相似，∠B＝∠B，∴分两种情况讨论：
【变式1】如图，在△ABC中，DE∥BC，DE＝2，BC＝5，则 S△ADE∶S△ABC的值是(　B　)
8字模型
(1)求证：△ADF∽△ECF；
(1)证明：∵四边形ABCD为平行四边形，∴AD∥BC，即AD∥CE. ∴∠DAF＝∠CEF，∠ADF＝∠ECF. ∴△ADF∽△ECF.
(1)求证：△DEF∽△BEC；
(2)若DE＝2，BE＝6，求⊙O的面积．
子母模型
(1)求证：△ACD∽△ABC；
(2)若AD＝3，BD＝2，求CD的长．
一线三等角模型
如图，在等边三角形ABC中，点P为BC上一点，点D为AC上一 点，且∠APD＝60°，2BP＝3CD，BP＝1.
(1)求证：△ABP∽△PCD；
(1)证明：∵△ABC是等边三角形，∴AB＝BC＝AC，∠B＝∠C＝60°. ∵∠BPA＋∠APD＋∠DPC＝180°，∠APD＝60°，∴∠BPA＋∠DPC＝120°. ∵∠DPC＋∠C＋∠CDP＝180°，∴∠DPC＋∠CDP＝120°. ∴∠BPA＝∠CDP. ∴△ABP∽△PCD.
(2)求△ABC的边长．
【变式5】如图，在四边形ABCD中，∠A＝∠B＝90°，点P为AB上 一点，连接PD，PC，∠DPC＝90°. (1)求证：△APD∽△BCP；
(1)证明：∵∠A＝90°，∠DPC＝90°，∴∠ADP＋∠DPA＝90°，∠DPA＋∠BPC＝90°. ∴∠ADP＝∠BPC. 又∠A＝∠B＝90°，∴△APD∽△BCP.
(2)若点P恰为AB的中点，且AB＝8，DA＝3，求PC的长．
手拉手模型
如图，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD. 若S△ABC∶S△DEC＝9∶16，△ABC的周长为9，则△DEC的周长 为 ⁠．