第十九章 一次函数 章节复习（课件）

这是一份第十九章 一次函数 章节复习（课件），共60页。
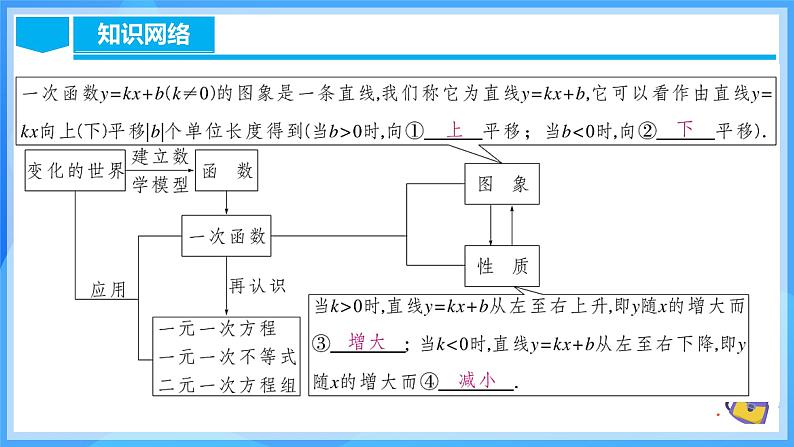
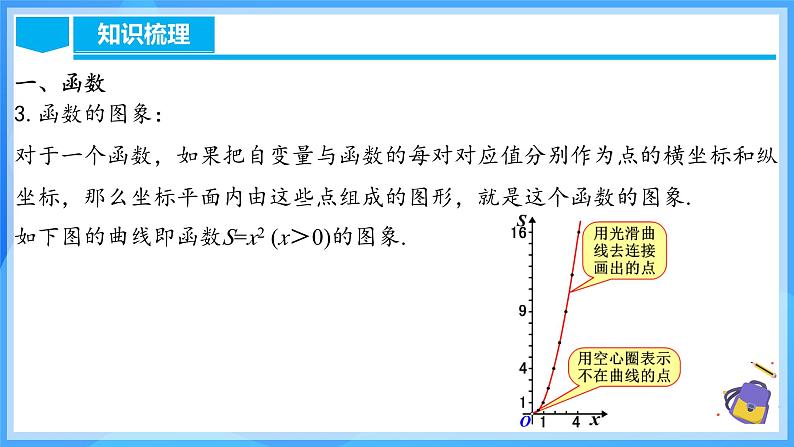
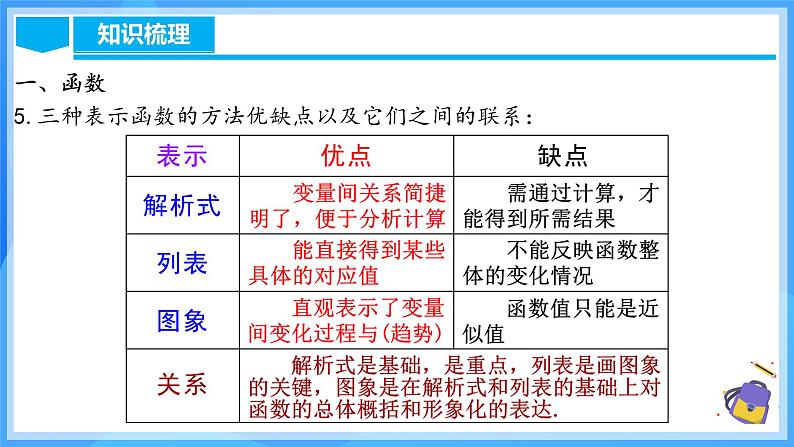
第十九章 一次函数人教版数学八年级下册章节复习目 录1 知识网络2 知识梳理3 考点梳理4 考点解析5 迁移应用1.回顾总结本章的知识点和知识结构;2.一次函数的定义、图象和性质的应用; (重点)3.运用函数思想解决实际问题;(难点)4.总结本章重要思想方法.一、函数1.变量和常量：变量：在一个变化过程中，数值发生变化的量为变量.常量：在一个变化过程中，数值始终不变的量为常量.2.函数：一般地，在一个变化过程中，如果有两个变量 x 与 y ，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说 x 是自变量，y 是 x 的函数.如果当 x = a 时 y = b，那么 b 叫做当自变量的值为 a 时的函数值.一、函数3.函数的图象：对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.如下图的曲线即函数S=x2 (x＞0)的图象.4.描点法画函数图象的一般步骤：第一步：列表---表中给出一些自变量的值及其对应的函数值；第二步：描点---在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点；第三步：连线---按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来.一、函数5.三种表示函数的方法优缺点以及它们之间的联系：一、函数二、一次函数一般地，形如y=kx(k是常数，k≠0)的函数，叫做正比例函数，其中k叫做比例系数.1.正比例函数：二、一次函数 一般地，正比例函数y=kx(k是常数，k≠0)的图象是一条经过原点的直线，我们称它为直线y=kx.当k＞0时，直线y=kx经过第三、第一象限，从左向右上升，即随着x的增大y也增大；当k＜0时，直线y=kx经过第二、第四象限，从左向右下降，即随着x的增大y反而减小.2.正比例函数的图象和性质：正比例函数y=kx(k≠0)的图象是经过原点和点(1，k)的一条直线.二、一次函数二、一次函数一般地，形如y=kx+b(k，b是常数，k≠0)的函数，叫做一次函数.特别注意：k≠0，自变量x的指数是1.当b=0时，y=kx+b就变成了y=kx，所以说正比例函数是一种特殊的一次函数.3.一次函数的概念：二、一次函数4.一次函数的图象的平移规律： 一次函数y=kx+b(k≠0)的图象也是一条直线，我们称它为直线y=kx+b，它可以看作由直线y=kx向上(或向下)平移|b|个单位长度而得到的. 当b＞0时，向上平移；当b＜0时，向下平移. 二、一次函数5.一次函数的图象和性质：三、用待定系数法求一次函数的解析式像这样，通过先设定函数解析式（确定函数模型），再根据条件确定解析式中的未知系数，从而求出函数解析式的方法称为待定系数法.三、用待定系数法求一次函数的解析式用待定系数法求一次函数解析式的一般步骤：（1）先设出函数解析式；（2）根据条件列关于待定系数的方程（组）；（3）解方程（组）求出解析式中未知的系数；（4）把求出的系数代入设的解析式，从而具体写出这个解析式.四、一次函数与方程、不等式1.一次函数与一元一次方程的关系四、一次函数与方程、不等式2.一次函数与一元一次不等式的关系四、一次函数与方程、不等式3.一次函数与二元一次方程组的关系由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组，都对应两个一次函数，于是也对应两条直线. 从“数”的角度看，解这样的方程组，相当于求自变量为何值时相应的两个函数值相等，以及这个函数值是多少；从“形”的角度看，解这样的方程组，相当于确定两条相应直线交点的坐标. 因此，我们可以用画一次函数图象的方法得到方程组的解.五、一次函数的实际应用01函数的有关概念及图象  例2.在全民健身环城越野赛中，甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米. 其中正确的说法有( )A.1个 B.2个 C.3个 D.4个C例3.如图，平面直角坐标系中，在边长为1的正方形ABCD的边上有一动点P沿A→B→C→D→A运动一周，则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )D【1-1】根据图中的程序，当输入数值x为-2时，输出数值y为______.6【1-2】小亮从家去学校，为了锻炼身体，一开始跑步前进,跑累了再步行走完余下的路程，下图中，纵轴表示离家的距离，横轴表示出发后的时间，则下列四个图象中较符合该学生走法的是( )C【1-3】小明同学骑自行车去郊外春游，如图表示他离家的距离y(km)与所用的时间x(h)之间关系的函数图象. （1）根据图象回答：小明到达离家最远的地方需______h；（2）小明出发2.5 h后离家_______km；（3）小明出发__________h后离家12 km. 322.52.5120.8或5.202正比例函数的图象与性质例4.已知正比例函数y＝(2m＋4)x.求：(1)m为何值时，函数图象经过第一、三象限； (2)m为何值时，y随x的增大而减小；(3)m为何值时，点(1，3)在该函数的图象上． 解：∵函数图象经过第一、三象限，∴2m＋4＞0，解得m＞－2.解：∵y随x的增大而减小，∴2m＋4＜0，解得m＜－2.例5.若正比例函数y＝(m﹣2)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1＜x2时，y1＞y2，则m的取值范围是（　　）A．m＞0 B．m＜0 C．m＞2 D．m＜2【解析】根据题意，知：y随x的增大而减小，则k＜0，即m﹣2＜0，m＜2．故选：D．D例6.如图，正比例函数y=kx的图象经过点A，点A在第四象限，且横坐标为3.过点A作AH⊥x轴，垂足为点H，且△AOH的面积为3.(1)求正比例函数的解析式; (2)在x轴上是否存在一点P，使△AOP的面积为5?若存在，求出点P的坐标；若不存在，请说明理由.  DB  D    03一次函数的图象与性质  C  C   例10.如图，正方形A1B1C1O， A2B2C2C1，A3B3C3C2， ...按其所示放置，点A1，A2，A3，…和C1，C2， C3，…分别在直线y=x+1和x轴上，则点B2025的横坐标是___________.【分析】当x=0时，y=x+1=1，∴A1(0,1)，B1(1，1)易得每一个正方形的边长都是它前一个正方形边长的2倍，因此B2的横坐标为1+1×2=1+2=3=22-1，B3的横坐标为1+1×2+2×2=1+2+4=7=23-1,B4的横坐标为24-1,…，B2025的横坐标为22025-1.22025-1 BC【3-3】已知一次函数y=2x-4.(1)画出它的图象; (2)写出函数图象与x轴、y轴交点的坐标;(3)求这条直线与两坐标轴所围成的三角形面积.   04一次函数的“图象共存”问题 B两个一次函数y1=ax+b和y2=bx+a (a≠b)在同一直角坐标系中的图象可能是( )A05待定系数法求一次函数解析式例12.若一次函数的图象经过点A(2，0)且与直线y=-x+3平行，求其解析式.解：设这个一次函数的解析式为y=kx+b.∵一次函数的图象与直线y=-x+3平行∴k=-1把A(2，0)代入y=-x+b中解得b=2∴一次函数的解析式为y=-x+2.例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6，相应函数值的取值范围是-5≤y≤-2，求这个函数的解析式.  例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6，相应函数值的取值范围是-5≤y≤-2，求这个函数的解析式.例14.如图，直线l与y轴交于点(0，3)，与正比例函数y=2x的图象交于点B，且点B的横坐标为1，求直线l对应的函数解析式. 【5-1】一次函数y=mx+|m-1|的图象经过点(0，2)，且y随x的增大而增大，则m的值是_____.【5-2】已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5，则此一次函数的解析式可能为__________________.3y=3x+3或y=-3x+3【5-3】已知一次函数的图象经过点(9，0)和点(24，20)，写出函数的解析式. 06一次函数的平移规律(上、下平移)  A DA【6-3】直线y=6x-5向上平移3个单位，则平移后的直线与y轴的交点坐标是_______.(0,-2)07一次函数与方程、不等式 A     【7-2】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k0；③当x