初中人教版（2024）17.1 勾股定理获奖教学作业ppt课件

这是一份初中人教版（2024）17.1 勾股定理获奖教学作业ppt课件，文件包含1713勾股定理的作图及典型计算pptx、1713勾股定理的作图及典型计算教学设计docx、1713勾股定理的作图及典型计算分层作业原卷版docx、1713勾股定理的作图及典型计算分层作业解析版docx、1713勾股定理的作图及典型计算导学案docx等5份课件配套教学资源，其中PPT共32页， 欢迎下载使用。
1.会运用勾股定理确定数轴上表示实数的点及解决网格问题.（重点）2.灵活运用勾股定理进行计算，并会运用勾股定理解决相应的折叠问题.（难点）
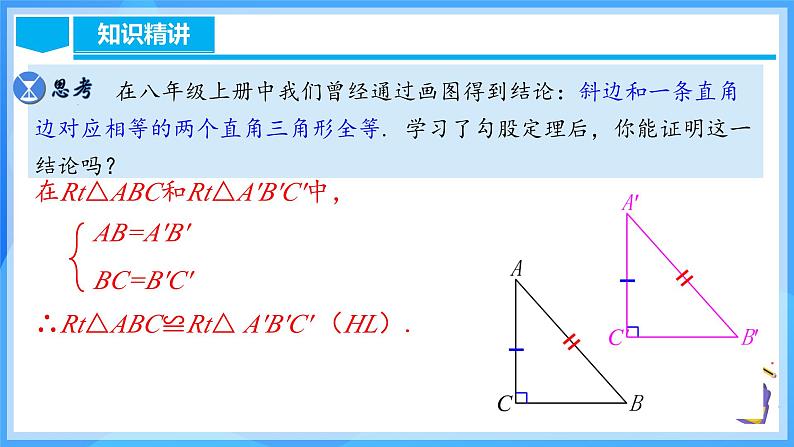
在八年级上册中我们曾经通过画图得到结论：斜边和一条直角边对应相等的两个直角三角形全等. 学习了勾股定理后，你能证明这一结论吗？
在Rt△ABC和Rt△A′B′C′中，
∴Rt△ABC≌Rt△ A′B′C′ （HL）.
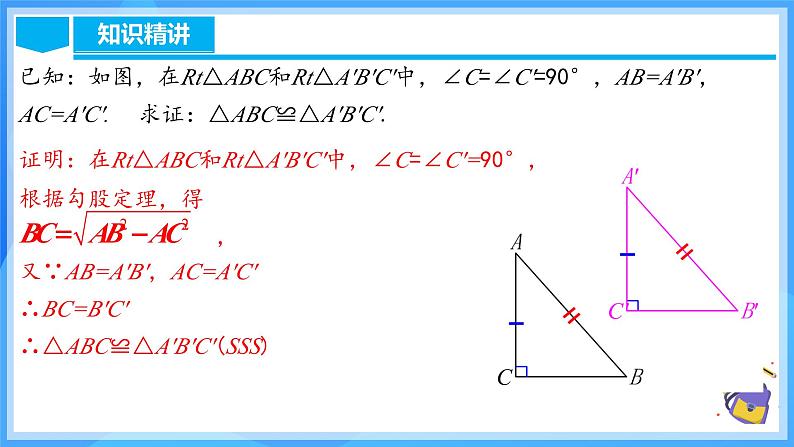
已知：如图，在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，AB=A′B′，AC=A′C′. 求证：△ABC≌△A′B′C′.
证明：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，根据勾股定理，得 ， 又∵AB=A′B′，AC=A′C′ ∴BC=B′C′ ∴△ABC≌△A′B′C′(SSS)
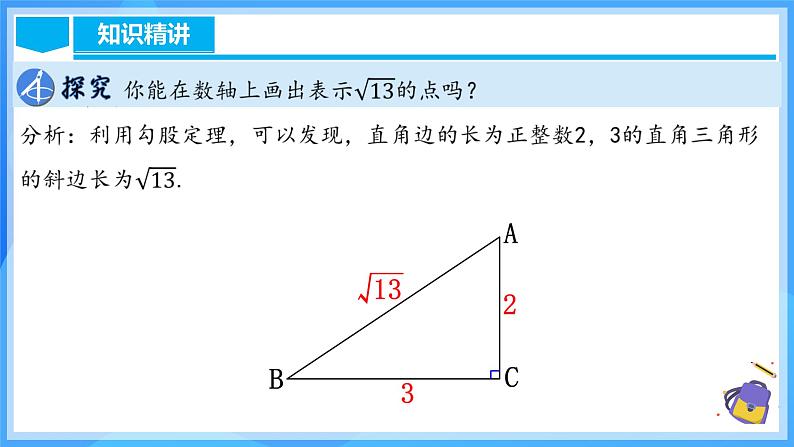
利用勾股定理表示无理数的方法:
（1）利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
（2）以原点为圆心，以无理数斜边长为半径画弧与数轴存在交点，在原点左边的点表示是负无理数，在原点右边的点表示是正无理数.
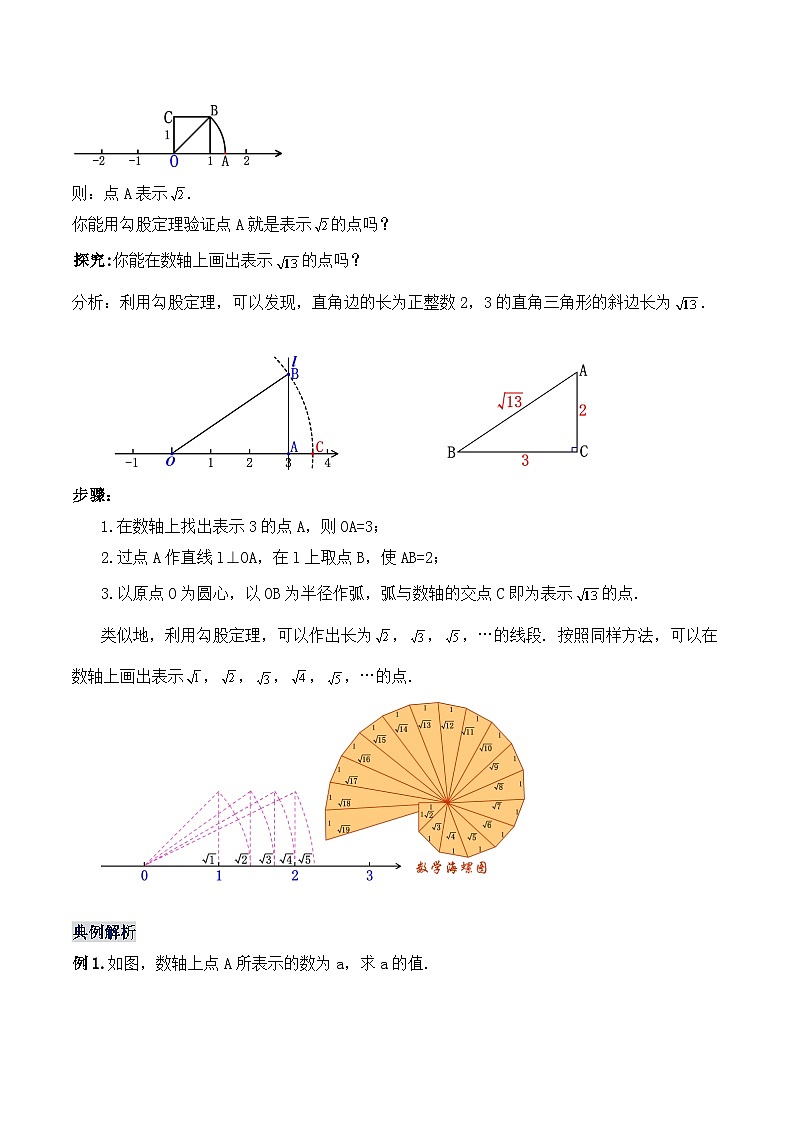
例1.如图，数轴上点A所表示的数为a，求a的值.
解：∵图中的直角三角形的两直角边为1和2，∴斜边长为 ，即－1到A的距离是 ，∴点A所表示的数为 .
【点睛】求点表示的数时注意画弧的起点不从原点起，因而所表示的数不是斜边长.
例2.在如图所示的6×8的网格中，每个小正方形的边长都为1，写出格点△ABC各顶点的坐标，并求出此三角形的周长．
解：由题图得A(2,2),B(-2,-1),C(3,-2).由勾股定理得∴△ABC的周长为
【点睛】勾股定理与网格的综合求线段长时，通常是把线段放在与网格构成的直角三角形中，利用勾股定理求其长度.
例3.如图，在2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，求AB边上的高.
解：如图，过点C作CD⊥AB于点D.
【点睛】此类网格中求格点三角形的高的题，常用的方法是利用网格求面积，再用面积法求高.
例4.如图，折叠长方形ABCD的一边AD，使点D落在BC边的F点处，若AB=8cm，BC=10cm，求EC的长.
解：在Rt△ABF中,由勾股定理得 BF2=AF2－AB2=102－82=36，∴BF=6cm.∴CF=BC－BF=4.设EC=xcm，则EF=DE=(8－x)cm ，在Rt△ECF中,根据勾股定理得 x2+42=(8－x)2，解得 x=3.即EC的长为3cm.
折叠问题中结合勾股定理求线段长的方法:(1)设一条未知线段的长为x(一般设所求线段的长为x)；(2)用已知线数或含x的代数式表示出其他线段长；(3)在一个直角三角形中应用勾股定理列出一个关于x的方程；(4)解这个方程，从而求出所求线段长.
例5.如图，四边形ABCD中∠A=60°，∠B=∠D=90°，AB=2，CD=1，求四边形ABCD的面积．
解：如图，延长AD、BC交于E．∵∠B=90°，∠A=60°，∴∠E=90°－60°=30°，在Rt△ABE和Rt△CDE中，∵AB=2，CD=1，∴AE=2AB=2×2=4，CE=2CD=2×1=2，由勾股定理得
3.如图，在平面直角坐标系中，点P的坐标为(-4,3),以点B(-1，0)为圆心，以BP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于( )A.-7和-6之间 B.-6和-5之间C.-5和-4之间 D.-4和-3之间
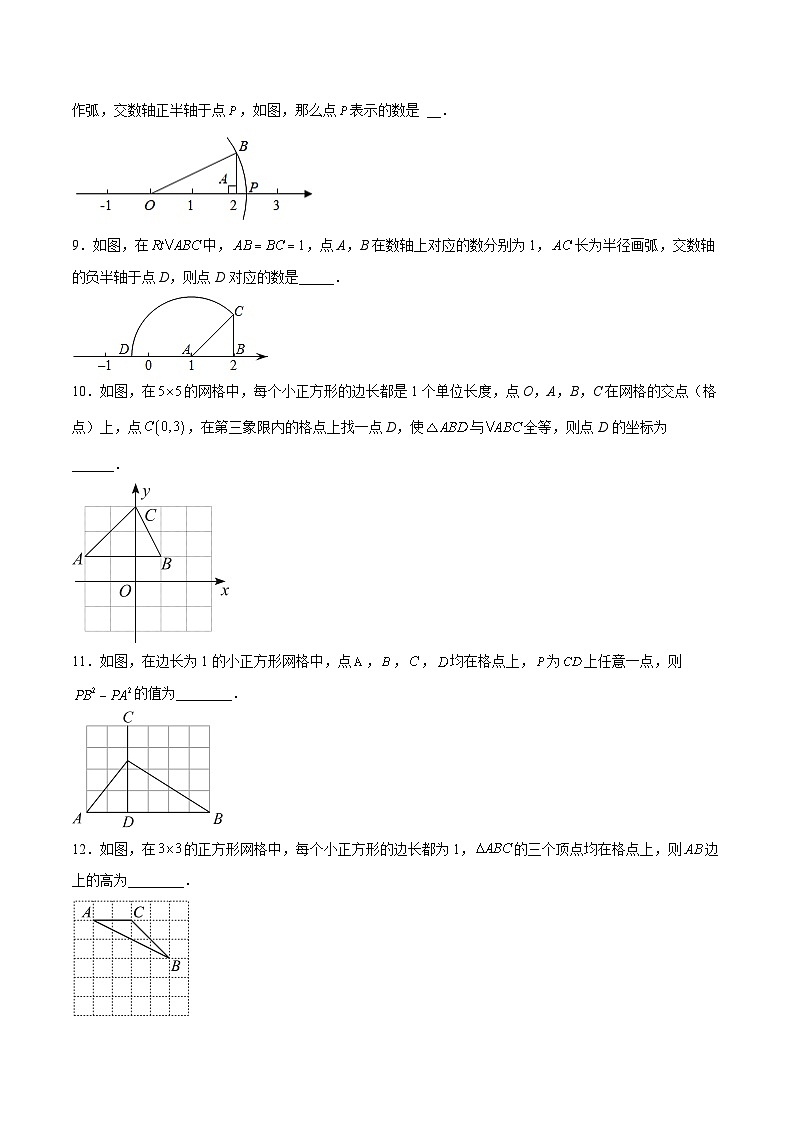
5.(1)如图①,把一个边长为2的正方形放在数轴上，以正方形的对角线为半径画弧交数轴于点A，则点A对应的数是______.(2)如图②，点P是以AB为半径的圆弧与数轴的交点，则数轴上点P表示的数是__________.
6.如图，已知长方形ABCD沿着直线BD折叠，使点C落在C'处，DC'交AB于E，AD=4, AB=8，则DE的长为_______.
解:如图所示，△ABC为所求.