初中数学人教版（2024）八年级下册18.1.1 平行四边形的性质评优课教学作业ppt课件

这是一份初中数学人教版（2024）八年级下册18.1.1 平行四边形的性质评优课教学作业ppt课件，文件包含1811平行四边形的性质1含动画演示pptx、1811平行四边形的性质1教学设计docx、1811平行四边形的性质1分层作业原卷版docx、1811平行四边形的性质1分层作业解析版docx、1811平行四边形的性质1导学案docx等5份课件配套教学资源，其中PPT共37页， 欢迎下载使用。
1.理解并掌握平行四边形的概念及掌握平行四边形的定义和对边相等、对角相等的两条性质.（重点）2.根据平行四边形的性质进行简单的计算和证明.（难点） 3.经历“实验—猜想—验证—证明”的过程,发展学生的思维水平.
这些生活中常见的平行四边形，你有注意到吗？
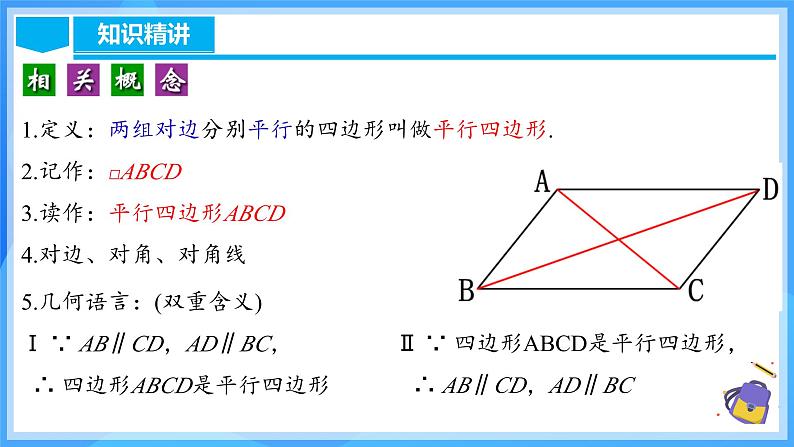
1.定义：两组对边分别平行的四边形叫做平行四边形.2.记作：□ABCD3.读作：平行四边形ABCD4.对边、对角、对角线
Ⅱ ∵ 四边形ABCD是平行四边形， ∴ AB∥CD，AD∥BC
5.几何语言：(双重含义)Ⅰ ∵ AB∥CD，AD∥BC， ∴ 四边形ABCD是平行四边形
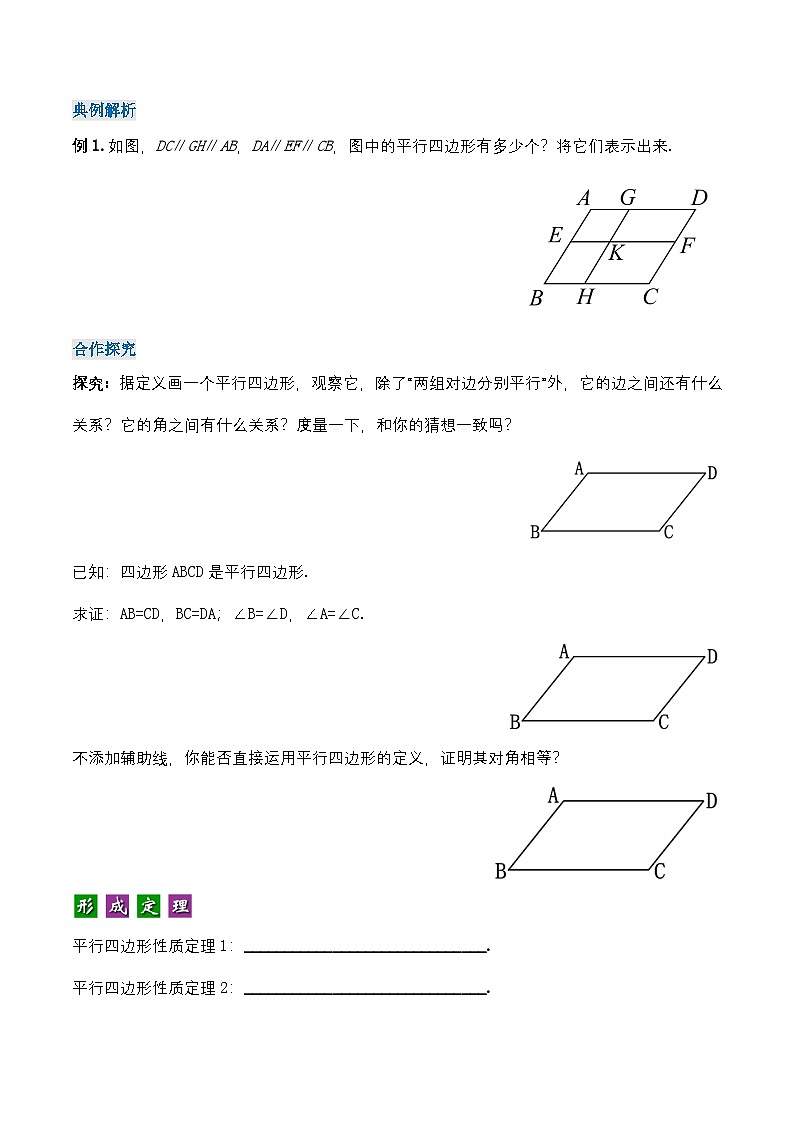
例1.如图，DC∥GH∥AB，DA∥EF∥CB，图中的平行四边形有多少个？将它们表示出来.
解：∵DC∥GH∥AB，DA∥EF∥CB，∴根据平行四边形的定义可以判定图中共有9个平行四边形，即□ AEKG，□ ABHG，□ AEFD，□ GKFD，□ BEKH，□ CHKF，□ BEFC，□ CDGH，□ ABCD.
【点睛】用定义判定平行四边形，即看四边形两组对边是否分别平行.
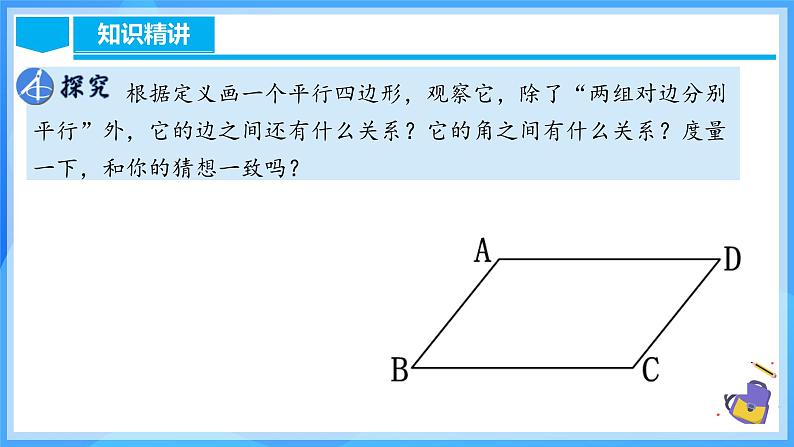
根据定义画一个平行四边形，观察它，除了“两组对边分别平行”外，它的边之间还有什么关系？它的角之间有什么关系？度量一下，和你的猜想一致吗？
平行四边形的对边相等；平行四边形的对角相等.
已知：四边形ABCD是平行四边形.  求证：AB=CD，BC=DA；∠B=∠D，∠A=∠C.
证明：连接AC∵ 四边形ABCD是平行四边形∴ AD∥BC，AB∥CD∴ ∠1=∠2，∠3=∠4又 AC是△ABC和△CDA的公共边∴ △ABC≌△CDA (ASA)∴ AB=CD，BC=DA，∠B=∠D又 ∵∠1=∠2，∠3=∠4∴ ∠1+∠4=∠2+∠3即 ∠BAD=∠DCB
证明：  ∵ 四边形ABCD是平行四边形  ∴ AD∥BC，AB∥CD  ∴ ∠B+∠A=180°，∠B+∠C=180°  ∴ ∠A=∠C  同理，∠B=∠D
平行四边形性质定理1：平行四边形的对边平行且相等;平行四边形性质定理2：平行四边形的对角相等.
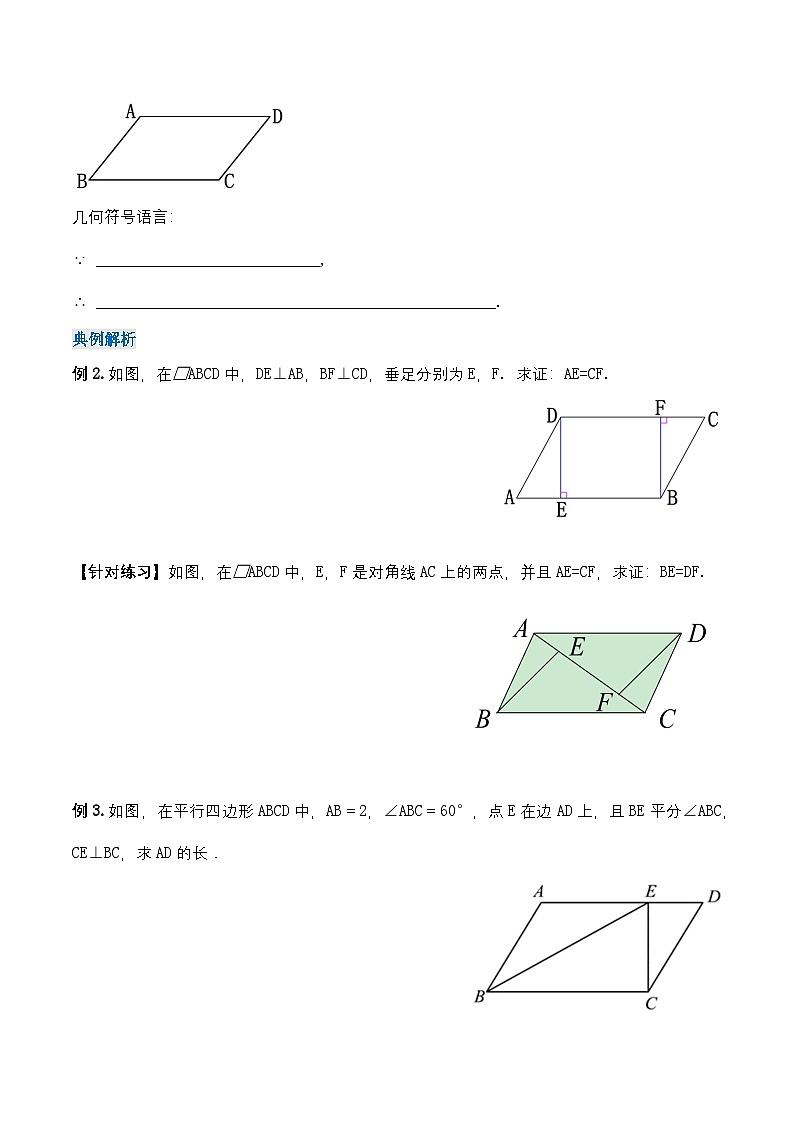
例2.如图，在□ ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F. 求证：AE=CF.
证明：∵ 四边形ABCD是平行四边形∴ ∠A=∠C，AD=CB∵ DE⊥AB，BF⊥CD∴ ∠AED=∠CFB=90°∴ △ADE≌△CBF (AAS)∴ AE=CF
证明：∵四边形ABCD是平行四边形，∴ AB=CD，AB∥CD∴∠BAE=∠DCF.又∵AE=CF，∴ △ABE≌△CDF.∴BE=DF.
如图，在□ ABCD中，E，F是对角线AC上的两点，并且AE=CF，求证：BE=DF.
例3.如图，在平行四边形ABCD中，AB＝2，∠ABC＝60°，点E在边AD上，且BE平分∠ABC，CE⊥BC，求AD的长．
∵AD∥BC∴∠AEB=∠CBE∴∠AEB=∠ABE∴AE＝AB=2．∴AD＝AE+DE=2+1=3
1.两点间的距离： ------连接两点的线段的长度.2.点到直线的距离： ------直线外一点到这条直线的垂线段的长度.
由平行四边
如图，a∥b，c∥d，c，d与a，b分别相交于A，B，C，D四点.
形的概念和性质可知，四边形ABDC是平行四边形，AB=CD.也就是说，两条平行线之间的任何两条平行线段都相等.
如果两条直线平行，那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线中，一条直线上任意一点到另一条直线的距离，叫做两条平行线间的距离.两条平行线间的距离处处相等.
点到直线的垂线段的长度
两条平行线中，从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
例4.如图，AB∥CD，BC⊥AB，若AB=4cm，S△ABC=12cm2，求△ABD中AB边上的高．
如图，剪两张对边平行的的纸条，随意交叉叠放在一起，重合的部分构成了一个四边形.转动其中一张纸条，线段AD和BC的长度有什么关系？为什么？
解：AD=BC.理由：两条平行线之间的任何两条平行线段都相等.
1.如图，在△ABC中，D, E, F分别在△ABC的三边上，且DE//BC， DF//AC,EF//AB,则图中平行四边形有( )A. 4个 B.3个 C.2个 D.1个2.已知□ ABCD的周长为32，AB=6, 则BC等于( )A.10 B.12 C.24 D.283.在□ ABCD中， ∠A:∠B:∠C:∠D的值可以是( )A.1:2:3:4 B.1:2:2:1 C.1:1:2:2 D. 2:1:2:1
4.如图，在□ ABCD中，AC的垂直平分线交AD于点E，连接CE.若□ ABCD的周长为32，则△CDE的周长为( )A.8 B.10 C.12 D. 165.如图,已知l1// l2, AB//CD, CE⊥l2，FG⊥l2,下列说法错误的是( )A.l1与l2之间的距离是线段FG的长度B.线段CD的长度就是l1与l2两条平行线间的距离C. AC=BDD. CE=FG
6. □ ABCD中，若∠B+∠D=260°，则∠A=______.7.将□ OABC放置在如图所示的平面直角坐标系中，点O为坐标原点.若点A的坐标为(3，0)，点C的坐标为(1，2),则点B的坐标为_________.
8.如图，□ ABCD的周长为20, AE平分∠BAD, CE=2， 则CD的长度为_____.9.如图，已知直线l1//l2， BC=3cm，S△ABC=3cm2， 则△BCD的边BC上的高是_____cm.
10.已知□ ABCD中，AE⊥BD，CF⊥BD,垂足为E、F,求证：BE=DF.
证明:∵四边形ABCD是平行四边形∴AB//CD，AB=CD∴∠ABD=2∠CDB∵AE⊥BD, CF⊥BD∴∠AEB=∠CFD=90°∴△ABE≌△CDF (AAS)∴BE=DF
11.已知,如图，在□ ABCD中，AE平分∠BAD交CD于点E, BF平分∠ABC交CD于点F，求证: DF=CE.
证明:∵四边形ABCD是平行四边形∴AB // CD，AD=BC∴∠BAE=∠DEA，∠ABF=∠CFB∵AE平分∠BAD,BF平分∠ABC∴∠BAE=∠DAE，∠ABF=∠CBF∴∠DEA=∠DAE，∠CFB=∠CBF∴AD=DE，BC=CF
∴DE=CF∴DE-EF=CF-EF即DF=CE .