数学八年级下册18.1.2 平行四边形的判定完整版教学作业课件ppt

这是一份数学八年级下册18.1.2 平行四边形的判定完整版教学作业课件ppt，文件包含1813平行四边形的判定1pptx、1813平行四边形的判定1教学设计docx、1813平行四边形的判定1分层作业原卷版docx、1813平行四边形的判定1分层作业解析版docx、1813平行四边形的判定1导学案docx等5份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
1.经历平行四边形判定定理的猜想与证明过程，体会类比思想及探究图形判定的一般思路；（重点）2.掌握平行四边形的三个判定定理，能根据不同条件灵活选取适当的判定定理进行推理论证.（难点）
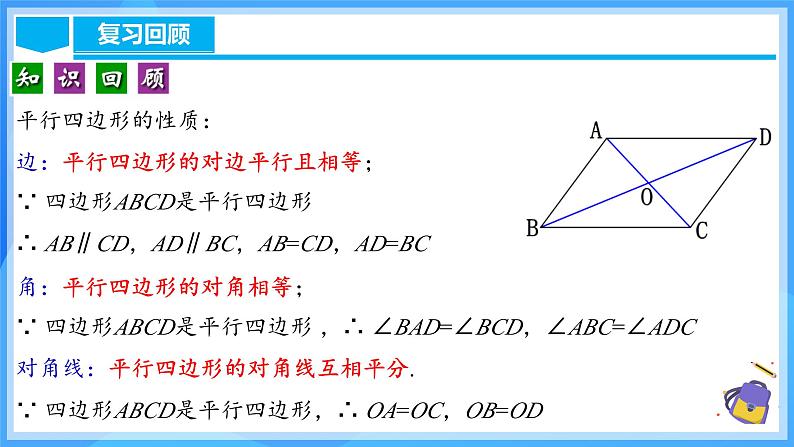
平行四边形的性质：边：平行四边形的对边平行且相等；∵ 四边形ABCD是平行四边形∴ AB∥CD，AD∥BC，AB=CD，AD=BC 角：平行四边形的对角相等；∵ 四边形ABCD是平行四边形 ，∴ ∠BAD=∠BCD，∠ABC=∠ADC对角线：平行四边形的对角线互相平分.∵ 四边形ABCD是平行四边形，∴ OA=OC，OB=OD
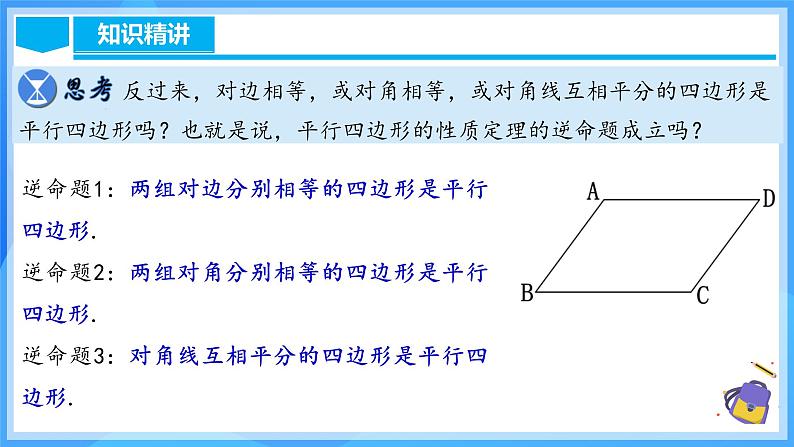
反过来，对边相等，或对角相等，或对角线互相平分的四边形是平行四边形吗？也就是说，平行四边形的性质定理的逆命题成立吗？
逆命题1：两组对边分别相等的四边形是平行四边形.逆命题2：两组对角分别相等的四边形是平行四边形.逆命题3：对角线互相平分的四边形是平行四边形.
逆命题1：两组对边分别相等的四边形是平行四边形.
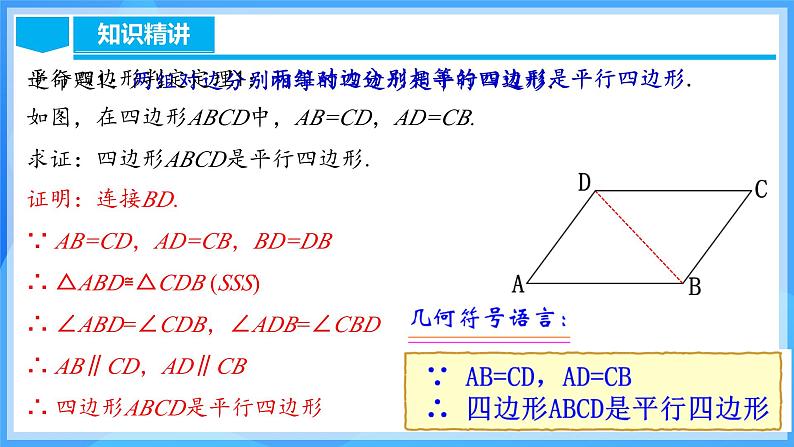
证明：连接BD.∵ AB=CD，AD=CB，BD=DB∴ △ABD≌△CDB (SSS)∴ ∠ABD=∠CDB，∠ADB=∠CBD∴ AB∥CD，AD∥CB∴ 四边形ABCD是平行四边形
如图，在四边形ABCD中，AB=CD，AD=CB.求证：四边形ABCD是平行四边形.
平行四边形判定定理1：两组对边分别相等的四边形是平行四边形.
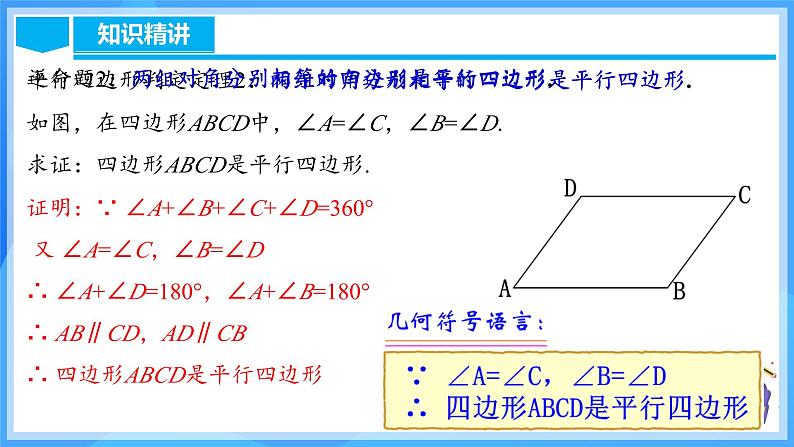
平行四边形判定定理2：两组对角分别相等的四边形是平行四边形.
如图，在四边形ABCD中，∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.
证明：∵ ∠A+∠B+∠C+∠D=360° 又 ∠A=∠C，∠B=∠D∴ ∠A+∠D=180°，∠A+∠B=180°∴ AB∥CD，AD∥CB∴ 四边形ABCD是平行四边形
逆命题2：两组对角分别相等的四边形是平行四边形.
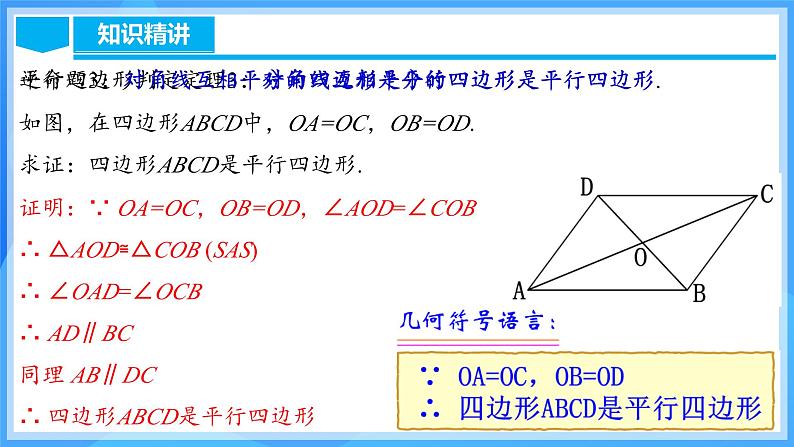
平行四边形判定定理3：对角线互相平分的四边形是平行四边形.
如图，在四边形ABCD中，OA=OC，OB=OD.求证：四边形ABCD是平行四边形.
逆命题3：对角线互相平分的四边形是平行四边形.
证明：∵ OA=OC，OB=OD，∠AOD=∠COB∴ △AOD≌△COB (SAS)∴ ∠OAD=∠OCB∴ AD∥BC同理 AB∥DC∴ 四边形ABCD是平行四边形
例1.如图，以△ABC的各边向同侧作正三角形，即等边△ABD、等边△ACE、等边△BCF，连接DF，EF.求证：四边形AEFD是平行四边形．
证明：∵△ABD和△BCF是等边三角形，∴∠DBF＋∠ABF＝∠ABC＋∠ABF＝60°， ∴∠DBF＝∠ABC.又∵BD＝BA，BF＝BC，∴△ABC≌△DBF(SAS)，∴AC＝DF.同理可证△ABC≌△EFC，∴EF＝AD，∴四边形AEFD是平行四边形．
如图，将□ ABCD的四边DA，AB，BC，CD分别延长至点E，F，G，H，使得AE=CG，BF=DH，连接EF，FG，GH，HE.求证:四边形EFGH为平行四边形.
证明:∵四边形ABCD是平行四边形∴AB=CD，∠BCD=∠BAD∴∠HCG＝∠FAE.∵BF＝DH，∴AF＝CH.又∵AE＝CG，∴△FAE≌△HCG(SAS)．∴EF＝GH.同理可得EH＝GF，∴四边形EFGH为平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°，∴∠D＝180°－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB，∴∠DAB＝∠1＋∠2＝125°.∵∠DCB＋∠DAB＋∠D＋∠B＝360°，∴∠DCB＝∠DAB＝125°.又∵∠D＝∠B＝55°，∴四边形ABCD是平行四边形．
例2.如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
如图，在□ ABCD中，∠DAB＝60°，点E，F分别在CD，AB的延长线上，且AE＝AD，CF＝CB.求证：四边形AFCE是平行四边形.
证明：∵四边形ABCD是平行四边形，∴DC∥AB，∠DCB＝∠DAB＝60°.∴∠ADE＝∠CBF＝60°.∵AE＝AD，CF＝CB，∴△AED，△CFB都是等边三角形．∴∠AEC＝∠BFC＝60°.又∵AF∥CE，∴∠EAF＝∠FCE＝120°.∴四边形AFCE是平行四边形．
例3.如图，□ ABCD的对角线AC、BD相交于点O，E、F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵ 四边形ABCD是平行四边形∴ AO=CO，BO=DO∵ AE=CF∴ AO-AE=CO-CF即 EO=FO又 BO=DO∴ 四边形BFDE是平行四边形
变式1：若E、F继续移动至OA、OC的延长线上，仍使AE=CF，则结论还成立吗?为什么?
解:四边形BFDE是平行四边形，理由如下:∵四边形ABCD是平行四边形∴AO=CO，BO=DO∵AE=CF ∴AO+AE=CO+CF即EO=FO又∵BO=DO∴四边形BFDE是平行四边形
变式2:问题中AE=CF，过点O作一直线分别交AB、CD于G、H，则四边形GFHE是平行四边形吗?为什么?
解:四边形GFHE是平行四边形，理由如下:∵四边形ABCD是平行四边形∴OA=OC，OB=OD∵AE=CF∴OA-AE=OC-CF，即OE=OF∵AB//CD ∴∠GBO=∠HDO又∵∠BOG=∠DOH ∴△BOG≌△DOH (ASA)∴OG=OH又∵OE=OF ∴四边形GFHE是平行四边形
1.下面给出四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是( )A.1:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:32.如图，在四边形ABCD中，AB=CD，BC=AD.若∠D=120°,则∠C的度数为( )A.60° B.70° C.80° D.90°
3.如图，在□ ABCD中，对角线AC、BD交于点O，E、F是对角线AC上的两点，给出下列四个条件:①AE=CF;②DE=BF;③∠ADE= ∠CBF;④∠ABE= ∠CDF.其中不能判定四边形DEBF是平行四边形的有( )A.0个 B.1个 C.2个 D.3个
4.四边形ABCD中，AB=9cm，BC=6cm，CD=9cm，当AD=____cm时，四边形ABCD是平行四边形.5.如图，在□ ABCD中，点E，F分别在边AD，BC上，且BE//DF,若AE=5，则CF=_____.6.如图，线段AB，CD相交于点O，且图上各点把线段AB,CD四等分，这些点可以构成平行四边形的个数是_____.
7.如图，在□ ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，求证:四边形KLMN为平行四边形.
证明:∵四边形ABCD是平行四边形∴AD=BC，AB=CD∠A=∠C，∠B=∠D∵AK=CM，BL=DN∴AB-AK=CD-CM，BC-BL=AD-DN 即BK=DM，CL=AN∴△AKN≌△CML，△BKL≌△DMN (SAS)∴KN=ML，KL=MN∴四边形KLMN是平行四边形
8.如图，在□ ABCD中，点E是边AD的中点，连接CE并延长交BA的延长线于点F，连接AC，DF.求证：四边形ACDF是平行四边形．
证明：∵四边形ABCD是平行四边形，∴AB∥CD.∴∠FAE＝∠CDE.∵E是AD的中点，∴AE＝DE.又∵∠FEA＝∠CED，∴△FAE≌△CDE(ASA)．∴EF＝EC.又∵AE＝DE，∴四边形ACDF是平行四边形．
9.如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE.(1)求证：AE＝BC；
证明：∵AB∥CD，∠B＝45°，∴∠C＋∠B＝180°∴∠C＝135°.∵DE＝DA，AD⊥CD，∴∠E＝45°.∵∠E＋∠C＝180°，∴AE∥BC.又AB∥CE.∴四边形ABCE是平行四边形，∴AE＝BC.
9.如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE.(2)若AB＝3，CD＝1，求四边形ABCE的面积．
解：∵四边形ABCE是平行四边形，∴AB＝CE＝3.∴AD＝DE＝CE－CD＝2.∴四边形ABCE的面积为3×2＝6.
10.如图，AC是平行四边形ABCD的一条对角线，BM⊥AC于M，DN⊥AC于N，四边形BMDN是平行四边形吗？说说你的理由．
解：四边形BMDN是平行四边形．理由如下：连接BD交AC于O．∵BM⊥AC于M，DN⊥AC于N，∴∠AND=∠CMB=90°．∵四边形ABCD是平行四边形，∴OB=OD，AO=CO，AD=BC，AD∥BC，∴∠DAN=∠BCM,∴△ADN≌△CBM，∴AN=CM，∴OA-AN=OC-CM，即ON=OM,∴四边形BMDN是平行四边形．
平行四边形判定定理1：两组对边分别相等的四边形是平行四边形.平行四边形判定定理2：两组对角分别相等的四边形是平行四边形.平行四边形判定定理3：对角线互相平分的四边形是平行四边形.