初中数学人教版（2024）八年级下册18.2.2 菱形优秀教学作业课件ppt

这是一份初中数学人教版（2024）八年级下册18.2.2 菱形优秀教学作业课件ppt，文件包含1823菱形的性质含动画演示pptx、1823菱形的性质教学设计docx、1823菱形的性质分层作业原卷版docx、1823菱形的性质分层作业解析版docx、1823菱形的性质导学案docx等5份课件配套教学资源，其中PPT共30页， 欢迎下载使用。
1.了解菱形的概念及其与平行四边形的关系.2.探索并证明菱形的性质定理.（重点）3.应用菱形的性质定理解决相关计算或证明问题.（难点）
前面我们学习了平行四边形和矩形，知道了矩形是由平行四边形角的变化得到，如果平行四边形有一个角是直角时，就成为了矩形.
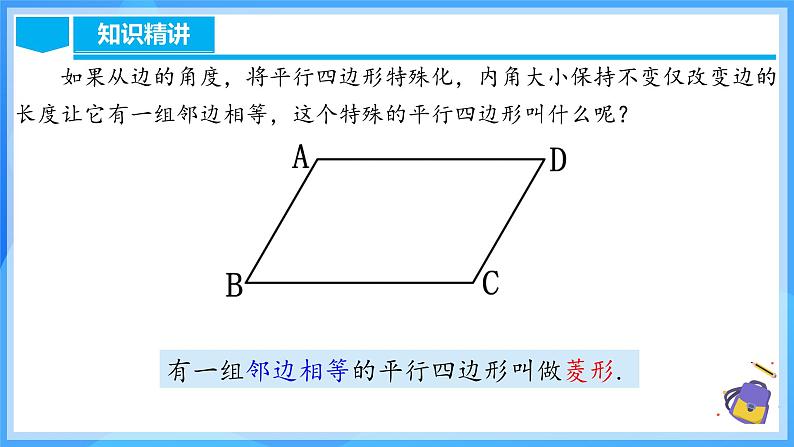
如果从边的角度，将平行四边形特殊化，内角大小保持不变仅改变边的长度让它有一组邻边相等，这个特殊的平行四边形叫什么呢？
有一组邻边相等的平行四边形叫做菱形.
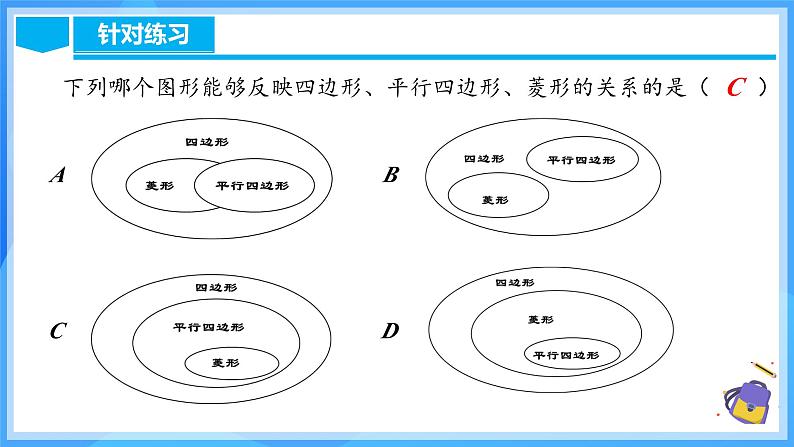
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是（ ）
将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开后你知道它是什么图形吗？
从中你能得到菱形的哪些性质？
菱形是轴对称图形，它的对角线所在的直线就是它的对称轴. 菱形还有以下性质： 菱形的四条边都相等； 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.
∵ 四边形ABCD是菱形∴ AB=BC=CD=AD，AC⊥BD AC平分∠BAD，AC平分∠BCD BD平分∠ABC，BD平分∠ADC
求证：菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.已知：如图，菱形ABCD的对角线相交于O点.求证：AC⊥BD，AC平分∠BAD和∠BCD，BD平分∠ABC和∠ADC.
证明：∵ 四边形ABCD是菱形∴ AB=AD，OB=OD∴ AC⊥BD，AC平分∠BAD (等腰三角形的三线合一)同理，AC平分∠BCD，BD平分∠ABC和∠ADC.
如图，比较菱形的对角线和平行四边形的对角线，我们发现，菱形的对角线把菱形分成四个全等的三角形，而平行四边形通常只被分成两对全等的三角形.
例1.如图，在菱形ABCD中，对角线AC、BD相交于点O，BD＝12cm，AC＝6cm，求菱形的周长．
四边形ABCD是菱形，对角线AC，BD相交于点O，且AB=5，AO=4.求AC和BD的长.
例2.如图，菱形花坛ABCD的边长为20m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长.
已知菱形的两对角线的长分别是6和8，求菱形的周长和面积.
例3.如图，E为菱形ABCD边BC上一点，且AB=AE，AE交BD于O，且∠DAE=2∠BAE，求证：OA=EB.
证明：∵四边形ABCD为菱形，∴AD∥BC，AD=BA， ∠ABC＝∠ADC＝2∠ADB ，∴∠DAE＝∠AEB，∵AB=AE,∴∠ABC＝∠AEB， ∴∠ABC=∠DAE， ∵∠DAE＝2∠BAE，∴∠BAE＝∠ADB. 又∵AD＝BA ，∴△AOD≌△BEA ，∴AO＝BE .
如图，在菱形ABCD中，CE⊥AB于E， CF⊥AD于F.求证:AE=AF.
证明:连接AC.∵四边形ABCD是菱形∴AC平分∠BAD,即∠EAC=∠FAC∵CE⊥AB,CF⊥AD∴∠AEC=∠AFC=90°又AC=AC∴△ACE≌△ACF (AAS)∴AE=AF
【点睛】菱形的面积计算有如下方法：(1)一边长与两对边的距离(即菱形的高)的积；(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍)；(3)两条对角线长度乘积的一半．
例4.如图，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．求：（1）两条对角线的长度；（2）菱形的面积．
【点睛】菱形中的相关计算通常转化为直角三角形或等腰三角形，当菱形中有一个角是60°时，菱形被分为以60°为顶角的两个等边三角形.
6.菱形的周长是8,则菱形的一边长是______.7.菱形的面积为24，一对角线长为6，则另一对角线长为_____，边长为_____.8.如图，一活动菱形衣架中，菱形的边均为16cm,若墙上钉子间的距离AB=BC=16cm，则∠1=______度.
9.如图，菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB 上，且BE=BO，则∠EOA=_____度.
10.如图，在边长为2的菱形ABCD中，∠ABC=120°，E，F分别为AD，CD上的动点，且AE+CF=2， 则线段EF长的最小值是______.
11.如图，在菱形ABCD中，E、F分别是BC、CD上的点，且BE=DF.求证:∠AEF=∠AFE.
证明:∵四边形ABCD是菱形∴AB=AD，∠B=∠D∵BE=DF∴△ABE≌△ADF(SAS)∴AE=AF∴∠AEF=∠AFE
12.如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，求证:∠DHO=∠DCO.
证明:∵四边形ABCD是菱形∴AC⊥BD,AB // CD,OB=OD∴∠DCO+∠CDO=90°,∠CDO=∠HBO∵DH⊥AB∴OH是Rt△BDH斜边BD上的中线∴OH=OB∴∠OHB=∠HBO ∴∠OHB=∠CDO∵∠DHO+∠OHB=90° ∴∠DHO=∠DCO
菱形是轴对称图形，它的对角线所在的直线就是它的对称轴. 菱形还有以下性质： 菱形的四条边都相等； 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.