初中数学人教版（2024）八年级下册18.2.2 菱形优秀教学作业课件ppt

这是一份初中数学人教版（2024）八年级下册18.2.2 菱形优秀教学作业课件ppt，文件包含1824菱形的判定含动画演示pptx、1824菱形的判定教学设计docx、1824菱形的判定分层作业原卷版docx、1824菱形的判定分层作业解析版docx、1824菱形的判定导学案docx等5份课件配套教学资源，其中PPT共33页， 欢迎下载使用。
1.经历菱形判定定理的探究过程，掌握菱形的判定定理．（重点）2.会用这些菱形的判定方法进行有关的证明和计算. （难点）
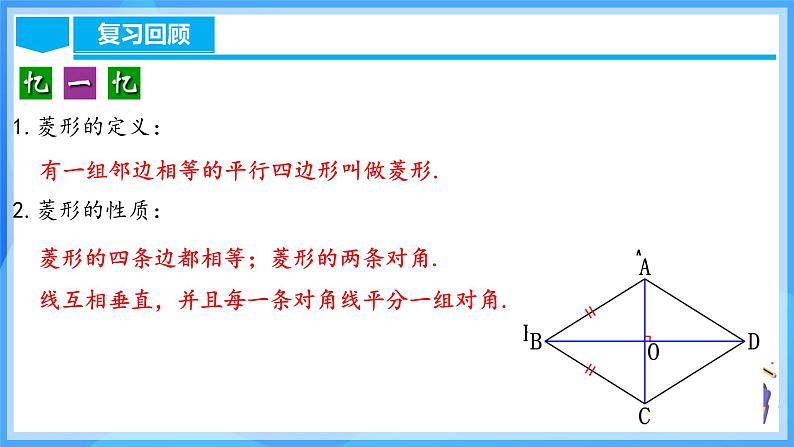
1.菱形的定义：2.菱形的性质：
有一组邻边相等的平行四边形叫做菱形.
菱形的四条边都相等；菱形的两条对角.线互相垂直，并且每一条对角线平分一组对角.
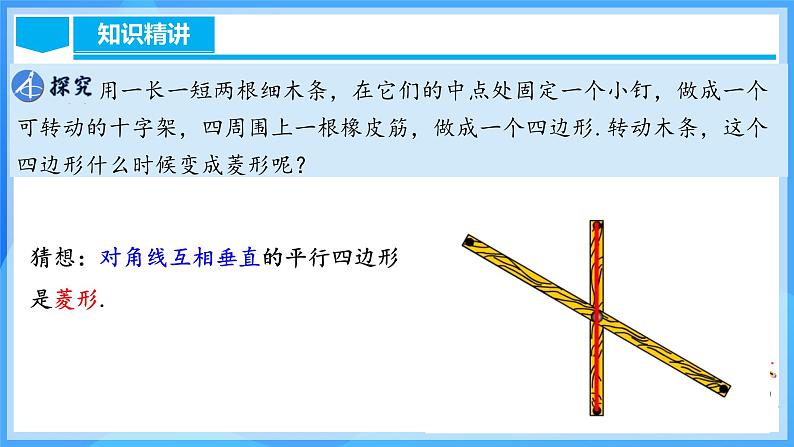
用一长一短两根细木条，在它们的中点处固定一个小钉，做成一个可转动的十字架，四周围上一根橡皮筋，做成一个四边形.转动木条，这个四边形什么时候变成菱形呢？
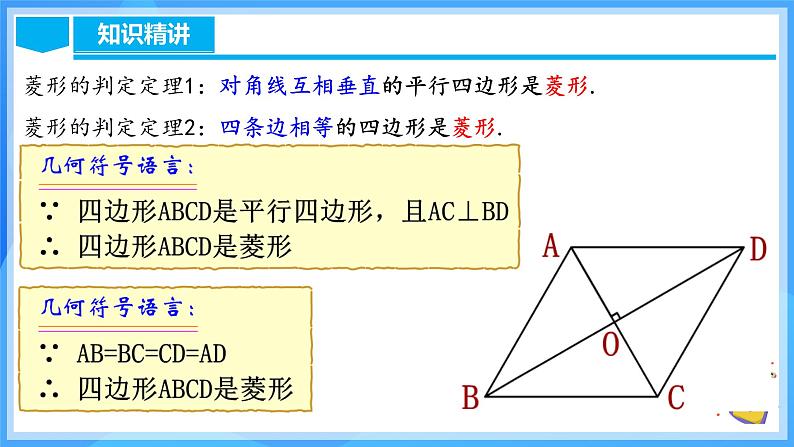
猜想：对角线互相垂直的平行四边形是菱形.
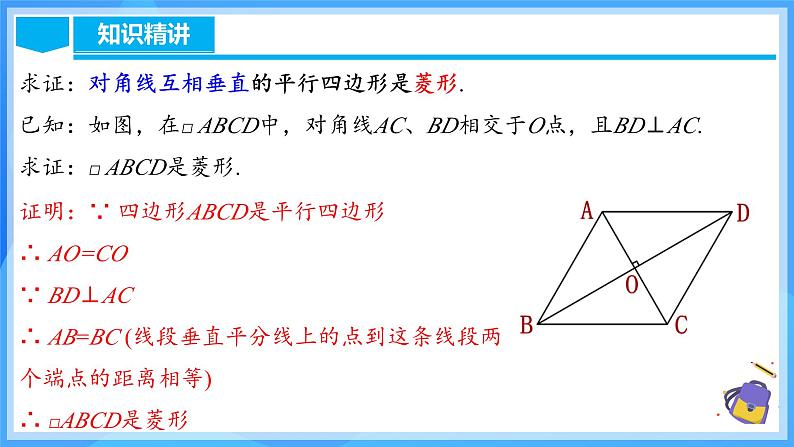
求证：对角线互相垂直的平行四边形是菱形.已知：如图，在□ ABCD中，对角线AC、BD相交于O点，且BD⊥AC.求证：□ ABCD是菱形.
证明：∵ 四边形ABCD是平行四边形∴ AO=CO∵ BD⊥AC∴ AB=BC (线段垂直平分线上的点到这条线段两个端点的距离相等)∴ □ABCD是菱形
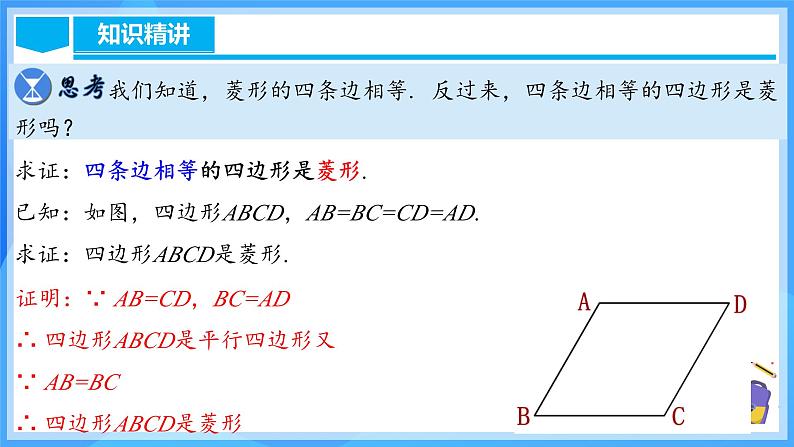
我们知道，菱形的四条边相等. 反过来，四条边相等的四边形是菱形吗？
求证：四条边相等的四边形是菱形.已知：如图，四边形ABCD，AB=BC=CD=AD.求证：四边形ABCD是菱形.
证明：∵ AB=CD，BC=AD∴ 四边形ABCD是平行四边形又∵ AB=BC∴ 四边形ABCD是菱形
菱形的判定定理1：对角线互相垂直的平行四边形是菱形.菱形的判定定理2：四条边相等的四边形是菱形.
例1.如图，□ ABCD的两条对角线AC、BD相交于点O，AB=5，AO=4，BO=3.求证：四边形ABCD是菱形.
证明：∵ AB=5，AO=4，BO=3∴ AB2=AO2+BO2        ∴ △OAB是直角三角形∴ AC⊥BD∴ □ ABCD是菱形
例2.如图，两张等宽的纸条交叉叠放在一起，重合的四边形ABCD是一个菱形吗？为什么？
解：四边形ABCD是菱形.理由如下：∵ AB∥CD，AD∥BC∴ 四边形ABCD是平行四边形过点A分别作BC，CD边上的高AE，AF，则AE=AF.∵ S□ABCD=BC×AE=CD×AF∴ BC=CD∴ 四边形ABCD是菱形
例3. 如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证：四边形AFCE是菱形．
证明: ∵四边形ABCD是矩形,∴AE∥FC，∴∠1=∠2.∵EF垂直平分AC，∴AO = OC . ∵∠AOE =∠COF，∴△AOE≌△COF，∴EO =FO.∴四边形AFCE是平行四边形.∵EF⊥AC∴ 四边形AFCE是菱形.
证明：∵ AD是角平分线， ∴∠1= ∠2,又∵AE=AC,AD=AD,∴ △ACD≌ △AED (SAS).同理△ACF≌△AEF(SAS) .∴CD=ED, CF=EF.又∵EF=ED,∴CD=ED=CF=EF,∴四边形ABCD是菱形.
如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.求证：四边形CDEF是菱形.
(1)求证：四边形EBFD为菱形；
1.平行四边形ABCD中，AC，BD是两条对角线，如果添加一个条件，即可推出平行四边形ABCD是菱形，以下哪个条件不符合要求( )A. AC⊥BD B. AC=BD C. AB=BC D. BC=CD2.顺次连接四边形ABCD各边的中点所得的四边形是菱形，则四边形ABCD一定是( )A.菱形 B.对角线互相垂直的四边形C.矩形 D.对角线相等的四边形
3.如图，AD是△ABC的中线，四边形ADCE是平行四边形，增加下列条件，能判定□ ADCE是菱形的是( )A.∠BAC=90° B.∠DAE=90° C. AB=AC D. AB=AE
5.如图，将等边三角形ABC沿射线BC向右平移到△DCE的位置，连接AD，BD，则下列结论:①AD=BC；②BD，AC互相平分；③四边形ACED是菱形.其中正确的是___________.
8.如图，在△ABC中，AD平分∠BAC，DF//AB，DE//AC.求证:四边形AEDF是菱形.
证明:∵DF//AB，DE//AC∴四边形AEDF是平行四边形∵AD平分∠BAC∴∠1=∠2∵DF//AB∴∠1=∠3∴∠2=∠3∴AF=DF∴四边形AEDF是菱形
9.如图，在矩形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点.求证:四边形EFGH是菱形.
证法一:∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=90°， AD=BC， AB=CD∵E、F、G、H分别是AB、BC、CD、AD的中点∴AH=DH=BF=CF，AE=BE=CG=DG∴△AHE≌△BFE≌△CFG≌△DHG (SAS)∴HE=EF=FG=GH∴四边形EFGH是菱形
10.如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE//AB交MN于E，连接AE、CD.(1)求证: AD=CE;(2)填空:四边形ADCE的形状是_______，并说明理由.
(1)证明:∵CE//AB∴∠DAO=∠ECO∵MN是AC的垂直平分线∴∠AOD=∠COE=90° ,AO=CO∴△AOD≌△COE (ASA)∴AD=CE
(2)理由:由(1)得AD=CE且AD//CE∴四边形ADCE是平行四边形又∵AC⊥DE∴四边形ADCE是菱形
11.如图，四边形ABCD是菱形，∠BAD=60°， 点H为对角线AC的中点，点E在AB的延长线上，CE⊥AB，点F在AD的延长线上，CF⊥AD.(1)求证:四边形CEHF是菱形;
11.如图，四边形ABCD是菱形，∠BAD=60°， 点H为对角线AC的中点，点E在AB的延长线上，CE⊥AB，点F在AD的延长线上，CF⊥AD.(2)若四边形CEHF的面积为18,求菱形ABCD的面积.