（寒假）新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直（2份，原卷版+教师版）

这是一份（寒假）新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直（2份，原卷版+教师版），文件包含寒假新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直原卷版doc、寒假新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直原卷版pdf、寒假新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直教师版doc、寒假新高考数学一轮复习考点精讲+随堂检测08空间中的平行与垂直教师版pdf等4份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。

考点01判断平行，垂直的有关命题
【例1】已知是两条不重合的直线，是两个不重合的平面，下列结论正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】C
【详解】对于A，，则可能平行、可能相交且不垂直，故A不正确；
对于B，，则可能平行、可能相交且不垂直、可能异面且不垂直，故B不正确；
对于C，若，根据线面垂直的性质定理可知，故C正确；
对于D，若，则或异面，故D不正确．故选：C．
【变式1】已知平面，直线，若且，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【详解】如下图且，，则l//a，此时，，所以，充分性不成立；

若，因为，所以，必要性成立，

故 “”是“”的必要不充分条件.故选：B.
【变式2】已知是两条不同的直线，，是两个不重合的平面，则有下列命题
①，，； ②，，；
③，，； ④，.
其中正确命题的个数为（ ）
A．0B．1C．2D．3
【答案】B
【详解】①若，，，则直线没有交点，异面或，故①不正确；
②若，，，当均与，的交线平行时，可得，故②不正确；
③若，，则，又，则，故③正确；
④若，，则或，故④不正确.其中正确命题的个数为.故选：B.
考点02平行的判定定理
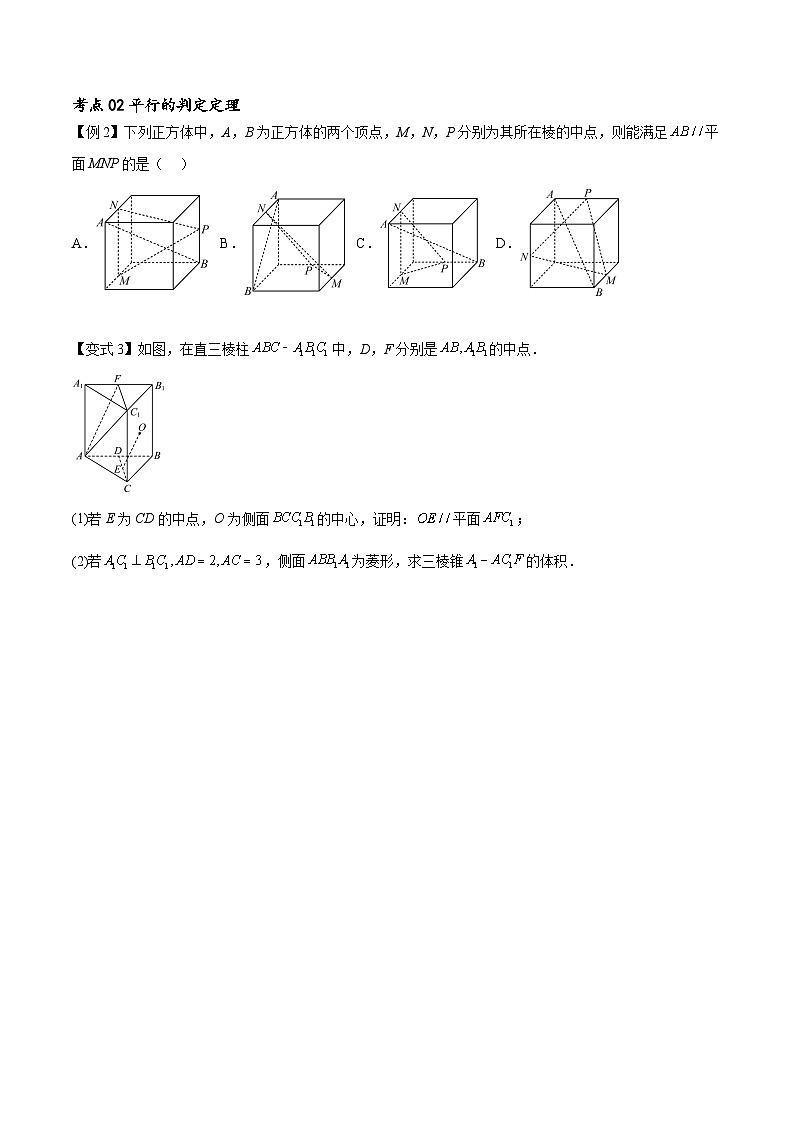
【例2】下列正方体中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，则能满足平面MNP的是（ ）
A． B． C． D．
【答案】C
【详解】对于A：连接，由图可知，与平面相交，故不满足平面，故A错误；

对于B：如图所示，分别是所在棱的中点，连接，则平面MNP和平面为同一平面，因为，因为与平面相交，所以不满足平面，故B错误；

对于C：连接，交与点，连接，因为，分别为中点，所以，由线面平行的判定定理可知，平面，故C正确；

对于D：分别是所在棱的中点，连接，，平面与平面为同一平面，取的中点为，连接，由中位线定理可知，，因为与平面相交，所以不满足平面，故D错误；

故选：C
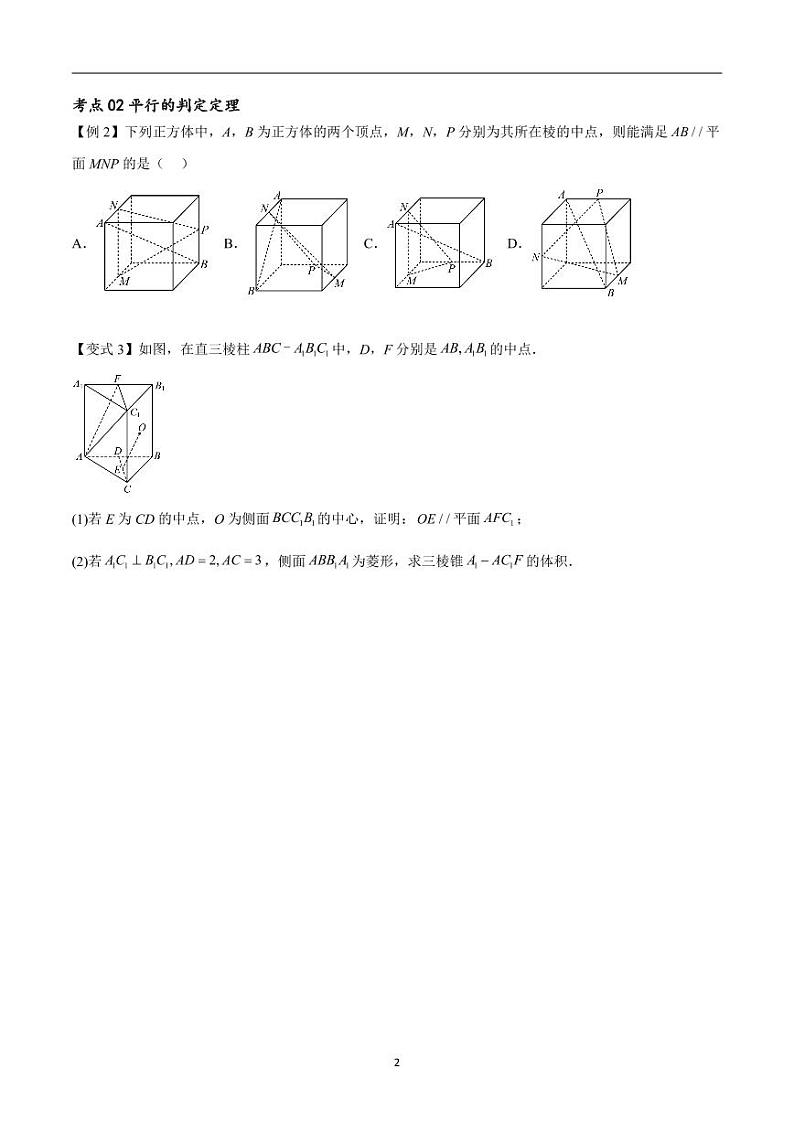
【变式3】如图，在直三棱柱中，D，F分别是的中点．

(1)若E为CD的中点，O为侧面的中心，证明：平面；
(2)若，侧面为菱形，求三棱锥的体积．
【答案】(1)证明见解析；(2)
【分析】（1）连接，，证得，进而证得，结合线面平行的判定定理，即可得证；
（2）根据题意，结合，利用锥体的体积公式，即可求解.
【详解】（1）证明：连接，．因为O为侧面的中心，且侧面为矩形，
所以O是的中点．因为为的中点，所以，
因为 分别是，的中点，且 且
所以，所以四边形是平行四边形，所以，
又因为，所以，平面，平面，所以平面.
（2）解：因为，且是的中点，且侧面为菱形，所以，
因为，所以，所以的面积，
在直三棱柱中，底面，所以.

考点03补全平行的条件
【例3】如图，在四棱锥中，底面，底面是矩形，.

(1)求点到平面的距离.
(2)若是的中点，是上靠近点的三等分点，棱上是否存在一点使平面？证明你的结论并求的长.
【答案】(1)；(2)存在满足条件的点，且点为线段上靠近点的三等分点.证明见解析，.
【分析】（1）法一：根据垂直关系分别求出以及，利用等体积转化法可求出点到平面的距离；法二：由条件可证明平面，从而点到平面的距离即为所求，在等腰直角中可求出结果；
（2）取点为线段上靠近点的三等分点，可证明平面平面，从而平面，结合三等分点即可求出结果.
【详解】（1）方法一：如图，连接，因为平面，
所以.
因为平面，平面，所以，
又平面PCD，所以平面，平面，
所以.设点到平面的距离为，则.
又因为，所以可得，得，即点到平面的距离为.
方法二：因为平面，所以平面，
所以点到平面的距离即点到平面的距离.作，垂足为.
同方法一可知平面，所以平面平面，且交线为，
又平面，所以平面，点到平面的距离即.
在等腰直角中，，所以，即点到平面的距离为.

（2）存在满足条件的点，且点为线段上靠近点的三等分点.
证明如下：连接交于点，连接.
因为点是的三等分点，所以为的中点，为的中点.
在矩形中，为的中点，所以，平面，所以平面，
因为点为的中点，所以，平面，
所以平面DEF ，又因为平面，所以平面平面，
又因为平面，所以平面，因为，所以.
考点04平行的性质定理
【例4】如图，在四棱锥中，底面ABCD为平行四边形，M为PA的中点，E是PC靠近C的一个三等分点．

(1)若N是PD上的点，平面ABCD，判断MN与BC的位置关系，并加以证明．
(2)在PB上是否存在一点Q，使平面BDE成立？若存在，请予以证明，若不存在，说明理由．
【答案】(1)，证明见解析
(2)存在，证明见解析
【分析】（1）．利用线面平行的性质定理可得答案；
（2）当Q是PB的中点时，平面BDE成立．由线面平行的判定定理可得平面BDE、平面BDE，再由面面平行的判定定理和性质定理答案.
【详解】（1），理由如下，
因为平面ABCD，平面PAD，平面平面，∴．
又因为，∴；
（2）当Q是PB的中点时，平面BDE成立，理由如下，
取PE的中点F，连接QF，又Q为PB的中点，∴．∵平面BDE，平面BDE，
∴平面BDE，连接AC交BD于点O，则O为AC的中点，又E是PC靠近C的一个三等分点，
∴E为CF的中点，∴，∵平面BDE，平面BDE，∴平面BDE，
又，∴平面平面BDE，
∵平面AQF，∴平面BDE．

考点05垂直的判定定理
【例5】如图，中，，是正方形，平面平面，若、分别是、的中点．

(1)求证：∥平面;
(2)求证：平面平面．
【分析】（1）取的中点，连接，，则由三角形中位线定理得∥，∥，再结合正方形的性质可得∥，则∥平面，由理∥平面，从而可证得平面∥平面，进而可证得结论；（2）由已知面面垂直可得平面，则，再由结合勾股定理逆定理可得，再由面线垂直和面面垂直的判定定理可证得结论.
【详解】（1）证明：如图，取的中点，连接，．
，分别是和的中点，∥，∥．
又四边形为正方形，∥，从而∥．
平面，平面，∥平面，
同理∥平面，又，平面，平面∥平面，
平面，则∥平面;

（2）为正方形，．
又平面平面，且平面平面，面，平面，
∵平面，∴，设，，，
∴，∴．又，，平面，
平面，而平面，∴平面平面．
考点06补全垂直的条件
【例6】在四棱锥中，是等边三角形，且平面平面，，．

(1).在AD上是否存在一点M，使得平面平面，若存在，请证明；若不存在，请说明理由；
(2).若的面积为，求三棱锥的体积．
【答案】(1)存在；证明见解析；(2)
【分析】（1）由题可得，即在上找一点M，使平面即可；
（2）设，由题目条件及的面积为，可得，即可得三棱锥的体积.
【详解】（1）存在，当M为的中点时，平面平面．
证明：取AD的中点M，连接，由是等边三角形，可得，
由平面平面，平面，平面平面，可得平面，
由平面，可得平面平面．
（2）设，可得，
则，由，可得，
由.
所以三棱锥P－ABC的体积为．
.
【变式5】如图，已知四棱锥的底面为等腰梯形，，与相交于点O，且顶点P在底面上的射影恰为O点．又．
(1)求异面直线与所成角的余弦值；
(2)求二面角的大小；
(3)设点M在棱上，且，问为何值时，平面．
【答案】(1)；(2)45°；(3)见解析.
【分析】（1）由已知得到PO⊥平面ABCD，利用线面垂直的性质得到PO⊥BD，过D做DE∥BC交于AB于E，连接PE，则∠PDE或其补角为异面直线PD与BC所成的角，利用平面几何即可得解；
（2）连接OE，由为等腰梯形，所以，且为中点，所以，又平面，∠PEO为二面角P﹣AB﹣C的平面角，然后求值即可；
（3）连接MD，MB，MO，利用PC⊥平面BMD，得到PC⊥OM，Rt△POC中求的PM＝，MC＝．
【详解】（1）∵PO⊥平面ABCD，∴PO⊥BD，又，
由平面几何可得：，过D做DE∥BC交于AB于E，连接PE，
则∠PDE或其补角为异面直线PD与BC所成的角，
∵四边形ABCD是等腰梯形，∴OC＝OD＝1，OB＝OA＝2，OA⊥OB，∴
又AB∥DC∴四边形EBCD是平行四边形．∴，∴E是AB的中点，且，
又，∴PEA为直角三角形，∴
在△PED中，由余弦定理得
故异面直线PD与BC所成的角的余弦值为；
（2）连接OE，由为等腰梯形，所以，且为中点，
所以，又平面，∠PEO为二面角P﹣AB﹣C的平面角，
∴sin∠PE0＝，∴∠PEO＝45°，∴二面角P﹣AB﹣C的平面角的大小为45°；
（3）连接MD，MB，MO，∵PC⊥平面BMD，OM⊂平面BMD，∴PC⊥OM，
在Rt△POC中，PC＝PD＝，OC＝1，PO＝，∴PM＝，MC＝，∴，
故λ＝时，PC⊥平面BMD．
考点07垂直的性质定理
【例7】如图，在三棱柱中，，分别为棱BC，的中点.

(1)求证: ∥平面；
(2)若平面平面，，，点满足，且，求实数的值.
【答案】(1)证明见解析；(2)3
【分析】（1）连接MN，则可得为平行四边形，再结合棱柱的性质可得四边形为平行四边形，则∥，再由线面平行的判定定理可得结论；
（2）取AB的中点，连接，则，再由面面垂直的性质可得平面ABC，则，连接，则，由线面垂直的判定可得平面，则，从而可得∥，进而可得结果.
【详解】（1）连接MN，因为，分别为棱BC，的中点，所以，
因为∥，，所以∥，，所以四边形为平行四边形，
所以∥，，又∥，，
所以∥，，所以四边形为平行四边形，
所以∥，又因为平面，平面，所以∥平面.
（2）解：取AB的中点，连接，因为，所以，
因为平面平面，平面平面，平面，所以平面ABC.
因为平面ABC，所以.连接，因为∥，，所以.
又，平面，所以平面.
因为平面，所以.又因为，所以，所以∥，
所以为MB的中点，即，所以.

考点08平行，垂直的综合应用
【例8】如图所示，在多面体中，四边形是正方形，是等边三角形，，且，，分别是，的中点.

(1)证明：平面平面；
(2)若平面平面，求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】（1）根据条件可以证明平面，平面，进而可以证明平面平面；
（2）利用条件可以求出到平面的距离，进而利用体积公式可以求出结果.
【详解】（1）因为，，是的中点，所以，且，
所以四边形是平行四边形，从而.
因为平面，平面，所以平面.
同理平面，又，所以平面平面.
（2）设的中点为，连接，则.

因为平面平面，
平面平面，平面，所以平面，
因为，平面，所以平面，
所以到平面的距离为，所以.
空间中的平行与垂直 随堂检测
1.设是两条不同的直线，是两个不同的平面，则下列结论中正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】D
【详解】对于A，若，则或，错误；
对于B，若，的位置关系不确定，可以平行、相交、异面直线，错误；
对于C，若，则或者相交，错误；
对于D，若，可得的方向向量分别是的法向量，因为，所以的法向量垂直，所以的方向向量垂直，则，正确.故选：D.
2.在直三棱柱中，是的中点．

(1)求证：//平面；
(2)求三棱锥的体积；
【答案】(1)证明见解析;(2)5
【分析】（1）借助题设条件运用线面平行的判定定理；（2）依据题设运用体积转换法进行探求．
【详解】（1）设，连接，由直三棱柱性质可知，侧面为矩形，

∴为中点， 又∵为中点，∴在中，，
又∵平面，平面，∴平面．
（2）由题，∴，即，
又由直三棱柱可知，侧棱底面，∴.
所以三棱锥的体积为5
3.如图，在四棱锥中，底面是正方形，底面ABCD，，点M是SD的中点，且交SC于点N.

(1)求证：平面ACM；
(2)求证：；
(3)求证：平面平面AMN.
【分析】（1）连结交于，连结，由的中位线定理，得，由此能证明结论；
（2）由线面垂直的判定定理可得平面，由线面垂直的性质可证得结论；
（3）由，，得平面，从而，由等腰三角形性质得，从而平面，进而，由证得面面垂直．
【详解】（1）连结交于，连结，

是正方形，是的中点．是的中点，是的中位线．．
又平面，平面，平面．
（2）是正方形，底面，底面，，
又平面，平面
平面，
（3）底面，底面，，
由正方形可得，又平面
平面，且平面，．
又，是的中点，．
又平面，平面．
平面，．由已知，
又平面，平面．
又平面，平面平面．