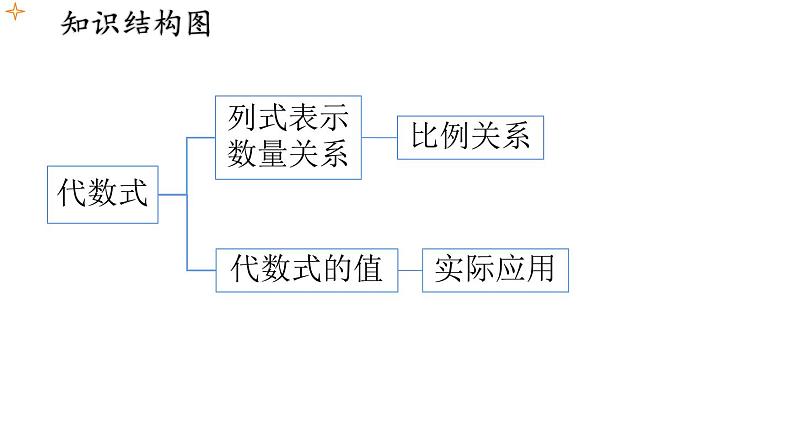
第三章 代数式 小结与复习 课件

这是一份第三章 代数式 小结与复习 课件，共20页。
人教版七年级(上)第三章 代数式小结与复习一、代数式1. 概念：用 把数或表示数的 连接起来 的式子，我们称为代数式.2. 书写规范： (1) 在含有字母的式子中如果出现乘号，通常将乘号 写作“·”或_________； (2) 除号用 代替； (3) 后面带单位的相加或相减的式子要 .运算符号省略不写分数线字母用括号括起来二、反比例关系 反比例关系：两个相关联的量，一种量变化，另一种量也随着变化，且这两个量中的 一定，这两个量就叫作 ，它们之间的关系叫作反比例关系.乘积成反比例的量三、代数式的值 1. 概念：一般地，用数值代替代数式中的字母，按照代数式中的运算关系计算得出结果，叫作代数式的值.2. 有些同类事物中的某种数量关系常常可以用公式来描述.例1 在 2x2，S = πr2，ab，a > 0，0， ，1 + 2 中，是代数式的有 ( )A. 5 个 B. 4 个 C. 3 个 D. 2 个√√√√√A代数式是用运算符号把数或表示数的字母连接起来的式子，注意不能含有 =、、≤、≥、≈、≠ 等符号.S = πr2，a > 0 中含有 = 和 >，不是代数式.下列各式中，符合代数式书写规则的是 ( )A. x×5 B. xy C. mn2 D. m÷nBA. 省略乘号，数字写在字母前面C. 数字写在字母前面D.除号用分数线代替5x2mn1.用代数式表示：(1)比a的3倍小4的数.(2)a的一半与b的和的平方.3a-4.2.说出下列各组代数式的意义有什么不同?(1)3x-4与3(x-4);(2)a2-b2与(a-b)2 .解：(1)3x-4的意义是x的3倍与4的差 3(x-4)的意义是x与4的差的3倍.(2) a2-b2的意义是a的平方与b的平方的差 或者a与b的平方的差， (a-b)2的意义是a与b的差的平方.例2 河上游的码头甲与下游的码头乙相距 s km，轮船在静水中的速度为 x km/h，水流的速度为 y km/h，则轮船从甲码头到乙码头往返一次航行所需时间 t = .顺水时逆水时船的速度＝船在静水中的速度＋水流速度船的速度＝船在静水中的速度－水流速度行船问题分析：长方形的周长为 20 米，其中一边长 x 米，则面积为 ( ) 平方米.A. x(20 - x) B. x(10 - x)C. x(20 - 2x) D. x(10 - 2x)Bxx 三个连续的偶数，中间的数是 a，则 a 的前边和后边分别是 _____ 和 _____.a - 2a + 2例3 （1）某校同学共同订购校服，小优发现随 的变化而变化，在变化过程中这两个量的 不变，即 不变，所以购买校服的总价和所订份数成 比例.（2）长方形的面积一定时，长与宽成 比例；长一定时，面积与宽成 比例.所订份数校服的总价比值单价正反正4. 观察并填写下表，然后回答问题.(1) 表中 和 是两种相关联的量；且这两种量中相对应的两个数的乘积都 ，这个积表示 ；(2) 因为 一定，所以 和 成反比例.方砖面积方砖数量相等铺地面积铺地面积方砖面积方砖数量6030156012660例4 若 a = 4，b = -2，求代数式 a - ab 的值.解：当 a = 4，b = -2 时，a - ab = 4 - 4×(-2) = 12.变式 若 |a| = 4，b = -2，则代数式 a - ab 的值为 .分析：|a| = 4→ a = ±4a - ab = (-4) - (-4)×(-2) = -12.±125. 已知：|x| = 3，|y| = 5，且 x < y，求 x - y 的值.解：因为 |x| = 3，|y| = 5，所以 x = ±3，y = ±5.因为 x < y，所以 x = ±3，y = 5.①当 x = 3，y = 5 时，②当 x = -3，y = 5 时，x - y = 3 - 5 = -2.x - y = (-3) - 5 = -8.综上所述，x - y 的值为 -2 或 -8.例5 某学校办公楼前有一块长为 m，宽为 n 的长方形空地，在中心位置留出一个半径为 a 的圆形区域建一个喷泉，两边是两块长方形的休息区，阴影部分为绿地.(1) 用含字母 a、b、m、n 的式子表示绿地面积；解：由图可知长方形空地面积为：mn，喷泉面积为：πa2，休息区面积为：2ab，所以绿地面积为：mn - πa2 - 2ab.(2) 当 m = 5，n = 4，a = 1，b = 2 时，绿地面积是多少 ( π 取 3 ) ?解：当 m = 5，n = 4，a = 1，b = 2 时，绿地面积为：mn - πa2 - 2ab=5×4 - 3×12 - 2×1×2 = 13.6. 如图，在一个长方形空地的四角都设计一块半径相同的四分之一圆形的花坛，其余地方铺草坪，若圆形的半径为 r 米，空地的长为 a 米，宽为 b 米.(1) 请列式表示草坪的面积；解：空地面积分别为 ab m2，花坛面积为：πr2 m2，所以草坪面积为：(ab - πr2) m2.(2) 若空地的长为 150 米，宽为 80 米， 圆形花坛的半径为 10 米，铺草坪每平方米需 20 元，花坛每平方米需 50 元，则完成这个设计一共需要多少元 ( π 取 3 )？花坛面积为：3×102 = 300 m2，解：当 a = 150，b = 80， r = 10 时，草坪面积为：150×80 - 3×102 = 11 700 m2.所以一共需要：11 700×20 + 300×50 = 249 000 (元).例6 如图，用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律，猜想第 10 个图中小正方形的个数为 .第 1 个图第 2 个图第 3 个图第 4 个图…2 + 3×13 + 4×24 + 5×35 + 6×411 + 12×102×3 - 13×4 - 14×5 - 15×6 - 111×12 - 11317. 用棋子摆出如图所示的一组 “口” 字，按照这种方法摆下去，则摆第 n 个 “口” 字需用棋子 ( )A. 4n 枚 B. n2 枚C. (4n - 4) 枚 D. (4n + 4) 枚A