湘教版（2024）七年级上册（2024）3.4 一元一次方程的应用课文配套ppt课件

这是一份湘教版（2024）七年级上册（2024）3.4 一元一次方程的应用课文配套ppt课件，文件包含34第1课时和差倍分问题pptx、34第1课时和差倍分问题docx等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
1. 分析实际问题中的数量关系，建立方程模型，解决实际问题.2. 领悟数学来源于生活，服务于生活，会用方程的思想解决实际生活中的问题.重点：找出等量关系，解决实际问题.难点：根据等量关系列出正确的一元一次方程.
探究 某文艺团体为“希望工程”募捐组织了一场义演，共售出 1000 张票，筹得票款 69500 元，其中成人票 80 元一张，学生票是 50 元一张，成人票与学生票各售出多少张？
某文艺团体为“希望工程”募捐组织了一场义演，共售出 1000 张票，筹得票款 69500 元，成人票与学生票各售出多少张？
成人票 80元/张
学生票 50元/张
成人票数＋__________＝1000 张；　 ①__________＋学生票款＝__________．②
分析题意可得此题中的等量关系有：
设售出的学生票为 x 张，填写下表：
根据等量关系②，可列出方程： .
解得 x＝ .
因此，售出学生票 张，成人票 张
成人票款＋学生票款＝69500元
50x + 80(1000－x) = 69500
可不可以设其他未知量？
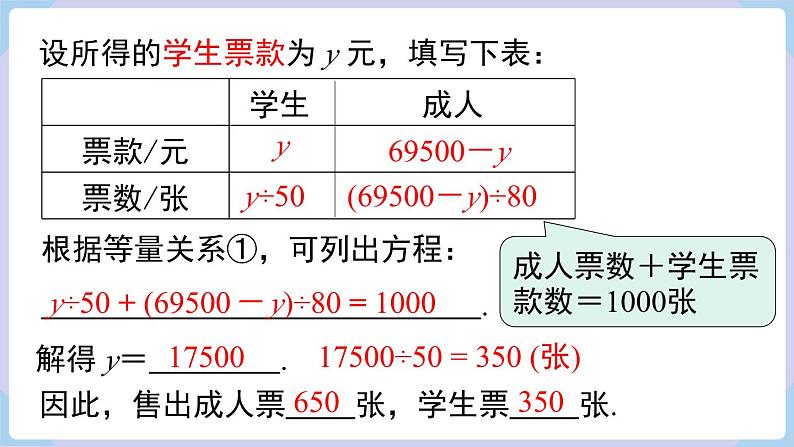
设所得的学生票款为 y 元，填写下表：
根据等量关系①，可列出方程： .
解得 y＝ .
因此，售出成人票 张，学生票 张.
(69500－y)÷80
y÷50 + (69500－ y)÷80 = 1000
成人票数＋学生票款数＝1000张
17500÷50 = 350 (张)
1. 当问题中含有两个未知量、两个等量关系时，可以把其中一个未知量设为未知数，另一个未知量 (根据其中一个等量关系) 用含未知数的代数式表示，而另一个等量关系则用来列方程.
2. 可以采用列表格的方法搞清较复杂问题中的各个量之间的关系.
例1 某房间里有 4 条腿的椅子和 3 条腿的凳子共 16 把，如果椅子腿数与凳子腿数的和为 60，试问：有几张椅子和几把凳子？
【分析】本问题中涉及的等量关系有： 椅子数 + 凳子数 = 16，椅子腿数 + 凳子腿数 = 60.
解：设有 x 张椅子，则有 (16 - x) 把凳子.
根据题意，得 4x + 3(16 - x) = 60.
移项、合并同类项，得 x = 12.
因此，凳子有 16 - 12 = 4 (把).
答：有 12 张椅子，4 把凳子.
去括号，得 4x + 48 - 3x = 60，
例2 某校七年级甲班有 45 人，乙班有 39 人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛，如果从甲班抽调的人比乙班多 1 人，那么甲班剩余人数恰好是乙班剩余人数的 2 倍. 请问：从甲、乙两班各抽调了多少人参加歌咏比赛?
【分析】本问题中涉及的等量关系有： (1) 甲班抽调的人数－乙班抽调的人数＝1； (2) 抽调后甲班剩余人数＝乙班剩余人数×2.
解：设从甲班抽调了 x 人，那么从乙班抽调了(x－1)人. 根据题意，得
45－x＝2[39－(x－1)].
解得 x＝35.
于是，x－1＝35－1＝34.
答：从甲班抽调了 35 人，从乙班抽调了 34 人参加歌咏比赛.
1. 一只轮船载重量为 300 吨，容积为 1000 立方米. 现有甲、乙两种货物待装，已知甲种货物每吨体积 7 立方米，乙种货物每吨体积 2 立方米，问怎样安排货运，才能充分利用船的载重量与容积？
解：设甲种货物运载 x 吨，则乙种货物为 (300 - x) 吨，甲种货物所占容积为 7x 立方米，乙种货物所占容积为 2(300 - x) 立方米，总容积为 1000 立方米.
根据题意，得 7x + 2(300 - x) = 1000.
解方程，得 x = 80. 300 - x = 220.
答：甲种货物装运 80 吨，乙种货物装运 220 吨.
例2 三个作业队共同使用水泵排涝，如果三个作业队排涝的土地面积之比为 4∶5∶6，而这一次装运水泵和耗用的电力费用共计 120 元，三个作业队按土地面积比各应负担多少元？
【分析】各个作业队应负担费用与排涝的土地面积成正比，且三个作业队各自应负担费用之和等于 120 元.由于共有土地 4 + 5 + 6 = 15 份，因而 120 元可由15份共同分担.
解：设每份土地排涝分担费用为 x 元，那么三个作业队应负担费用分别为 4x 元，5x 元，6x 元.
依据题意，得 4x + 5x + 6x = 120.
解方程，得 x = 8.
4x = 32，5x = 40，6x = 48.
答：三个作业队各应负担 32 元、40 元、48 元.
2. 质量为 45 克的某种三色冰淇淋中，咖啡色、红色和白色配料的比为 1∶2∶6，这种三色冰淇淋中，咖啡色、红色和白色配料分别是多少?
解：设咖啡色配料为 x 克，那么红色配料为 2x 克，白色配料为 6x 克.
依据题意，得 x + 2x + 6x = 45.
解方程，得 x = 5.
2x = 10，6x = 30.
答：咖啡色、红色和白色配料分别为 5克、10克、30克.
比例问题：就是把一个数按照一定的比分成若干份.一般需间接设元，设每一份为 x，再根据各部分之和等于总体列出方程.
例3 某车间有 29 名工人生产螺栓和螺母，每人每小时平均能生产螺栓 15 个或螺母 21 个，应如何分配生产螺栓和螺母的工人，才能使螺栓和螺母正好配套(两个螺栓配三个螺母) ?
【分析】本题有两个等量关系值得关注，一是总人数：生产螺母人数＋生产螺栓人数＝29；二是零件的配套关系：螺栓数∶螺母数＝2∶3.
解：设安排 x 人生产螺栓，则 (29－x) 人生产螺母． 根据题意得 解得 x＝14. 29－x＝15.答：安排 14 人生产螺栓，15 人生产螺母才能使螺栓 和螺母正好配套．
3. 七年级 (1) 班 43 人参加运土劳动，共有 30 根扁担，可两人用一根扁担抬土，也可一人用一根扁担挑土.
(1) 要安排多少人抬土，多少人挑土，可使扁担和人数 相配不多不少？
(2) 如果参加劳动的人数不变，扁 担数为 20 根可以吗？为什么？
答案：(1) 要安排 26 人抬土，17 人挑土.
(2) 不可以. 因为挑土人数不能为负数.
注意检验，结果要符合实际意义！
运用一元一次方程模型解决实际问题的步骤有哪些？
方法：采用间接设元法，通常设每一份为 x.
1.设未知数；2.找等量关系；3.列方程；4.解方程；5.检验作答
方法：设其中一个未知量为 x，用含 x 的代数式表示另一个未知量
1. 甲、乙二人按照 2∶5 的比例投资开办了一家公司，约定除去各项支出外，所得利润按投资比例分成，第一个月盈利 3500 元，那么甲得 ，乙分别应得 .
2. 一个两位数，个位数字和十位数字的和为 7，如果把十位数字和各位数字对调，所得新数比原数大 45，则原两位数是 .
3. 父子两人今年年龄之和为 40 岁，已知两年前父亲年龄是儿子年龄的 8 倍，请问两年前父子各几岁？