人教版2024-2025学年九年级上学期期末质量监测数学试卷（含答案）

这是一份人教版2024-2025学年九年级上学期期末质量监测数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
考试时间120分钟，试卷满分120分.
考生注意：请在答题卡各题目规定答题区内作答，答在本试卷上无效.
第一部分 选择题(共30分)
一、选择题(本题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的)
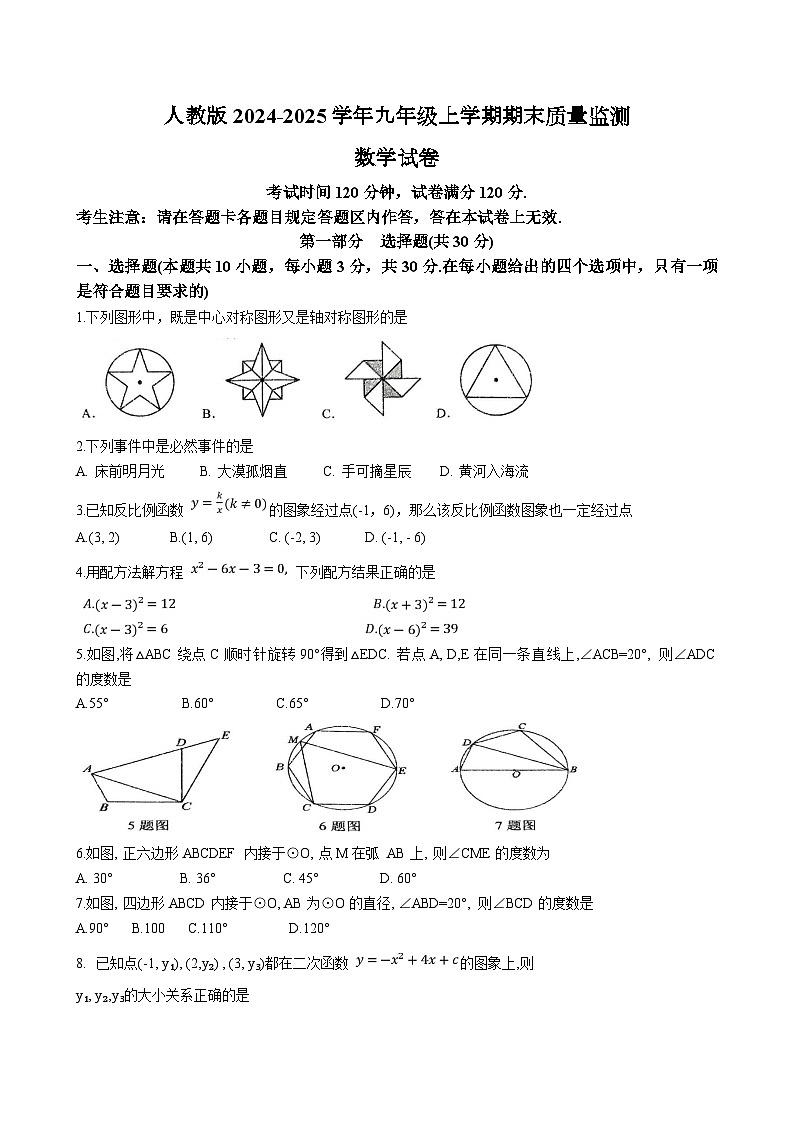
1.下列图形中，既是中心对称图形又是轴对称图形的是
2.下列事件中是必然事件的是
A. 床前明月光 B. 大漠孤烟直 C. 手可摘星辰 D. 黄河入海流
3.已知反比例函数 的图象经过点(-1，6)，那么该反比例函数图象也一定经过点
A.(3, 2) B.(1, 6) C. (-2, 3) D. (-1, - 6)
4.用配方法解方程 下列配方结果正确的是


5.如图,将△ABC绕点C顺时针旋转90°得到△EDC. 若点A, D,E在同一条直线上,∠ACB=20°, 则∠ADC 的度数是
A.55° B.60° C.65° D.70°
6.如图, 正六边形ABCDEF 内接于⊙O, 点M在弧 AB上, 则∠CME的度数为
A. 30° B. 36° C. 45° D. 60°
7.如图, 四边形ABCD内接于⊙O, AB为⊙O的直径, ∠ABD=20°, 则∠BCD的度数是
A.90°B.100C.110° D.120°
已知点(-1, y₁), (2,y₂) , (3, y₃)都在二次函数 的图象上,则
y₁, y₂,y₃的大小关系正确的是


9.近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动. 某款燃油汽车今年3月份售价为23万元，5月份售价为16万元. 设该款汽车这两个月售价的月均下降率是x，则所列方程正确的是

D. 23(1-2x)=16
10.我们定义一种新函数：形如y )的函数叫做“鹊桥”函数. 小丽同学画出了“鹊桥”函数. 的图象(如图所示)，并写出下列五个结论：其中正确结论的个数是
①图象与坐标轴的交点为 ( - 1, 0), (3, 0) 和 (0, 3);
②图象具有对称性，对称轴是直线x=1；
③当-1≤x≤1 或x≥3 时, 函数值y随x值的增大而增大;
④当x=-1或x=3时, 函数的最小值是0;
⑤当x=1时，函数的最大值是4
A. 4个 B. 3个 C. 2个 D. 1个
第二部分非选择题(共90分)
二、填空题：(本题共5小题，每小题3分，共15分)
11.已知x=1是一元二次方程. 的一个根，则另一个根为 ▲ .
12.在2×1的正方形网格格点上放三枚棋子，按如图所示的位置已放置了两枚棋子，若第三枚棋子随机放在其他格点上，则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 .
13.若正方形的边长为6，则其外接圆的半径为 ▲ .
14.小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m，水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为 其中x(m)是水柱距喷水头的水平距离，y(m)是水柱距地面的高度，则抛物线的表达式为
15.如图，在平面直角坐标系中，经过点A 的双曲线 同时经过点 B，且点A在点 B 的左侧, 点 A 的横坐标为1, ∠AOB=∠OBA=45°, 则k的值为 ▲ .
三、解答题：(本题共8小题，共75分.解答应写出文字说明、演算步骤或推理过程)
16.解下列方程: (每小题5分, 共 10分)

17.(本小题8分)二十四节气是中国古代一种用来指导农事的补充历法，在国际气象界被誉为“中国的第五大发明”，并位列联合国教科文组织人类非物质文化遗产代表作名录. 小明和小亮对二十四节气非常感兴趣，在课间玩游戏时，准备了四张完全相同的不透明卡片，卡片正面分别写有“A. 惊蛰” “B. 夏至” “C. 白露” “D. 霜降”四个节气，两人商量将卡片背面朝上洗匀后，从中随机抽取一张，并讲述所抽卡片上的节气的由来与习俗.
(1) 小明从四张卡片中随机抽取一张卡片，抽到“A. 惊蛰”的概率是 ；
(2) 小明先从四张卡片中随机抽取一张，小亮再从剩下的卡片中随机抽取一张，请用列表或画树状图的方法，求两人都没有抽到“B. 夏至”的概率.
18.(本小题8分) 如图，在平面直角坐标系中， 的顶点坐标分别为 (每个小方格都是边长为1个单位长度的正方形).
(1) 请画出 关于原点对称的 并写出 的坐标；
(2) 请画出 绕点B逆时针旋转 后的 ，并求出边AB扫过的面积.
19. (本小题8分) 如图，反比例函数 与一次函数 的图象交于点A (1, 3), 点B (n, 1), 一次函数. 与y轴相交于点 C.
(1) 求反比例函数和一次函数的表达式；
(2) 连接OA、OB, 求 的面积；
(3) 请直接写出关于x的不等式 的解集.
20.(本小题8分) 某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系：当销售单价为22元时，销售量为36本； 当销售单价为24元时，销售量为32本.
(1) 求出y与x的函数关系式并写出自变量的取值范围；
(2)当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大? 最大利润是多少?
21. (本小题8分)如图①，独轮车俗称“手推车”，又名辇、鹿车等，是交通运输工具史上的一项重要发明，至今在我国农村和一些边远地区仍然广泛使用. 如图②所示为从独轮车中抽象出来的几何模型. 在 中，以 的边AB为直径作⊙O, 交 AC于点 P, ∠A=∠C, 且PD⊥BC, 垂足为点 D.
(1) 求证: PD是⊙O 的切线;
(2) 若 求弧BP的长.
22. (本小题12分)
如图, △ABC与△CDE 是等边三角形, 连接AD, 取AD的中点P, 连接BP 并延长至点 M, 使 PM=BP, 连接 AM, EM, AE, 将 绕点 C 顺时针旋转.
【特例感知】
(1) 如图①, 当点D在BC上, 点E在AC上时, 则 的形状为 ；
【类比迁移】
(2) 当△CDE绕点C顺时针旋转至图②的位置时，此时点 E在线段BC的延长线上，请判断△AEM 的形状，并说明理由；
【方法运用】
(3) 若 将△CDE 由图①位置绕点 C 顺时针旋转( 当 时，请直接写出α的值.
23.(本小题13分)
我们把函数图象上横坐标与纵坐标互为相反数的点定义为这个函数图象上的“互反点”.例如二次函数 的图象上，存在一点 P(-1，1)，则点 P为二次函数 图象上的“互反点”.
(1) 分别判断 的图象上是否存在“互反点”.如果存在，请求出“互反点”的坐标； 如果不存在，请说明理由.
(2) 设函数 象上的“互反点”分别为 A，B，过点 B作 轴，足为点C，当 的面积为4时，求b的值.
(3) 若二次函数 的图象上有且只有一个“互反点”(2，-2) .
①求该二次函数的表达式；
②当1≤x≤t时, 二次函数 的最小值为 最大值为0，求t 的取值范围.
九年级数学参考答案及评分标准
一、选择题：
二、填空题：11．； 12．； 13． 14．【或者】；15．
三、解答题：
16．解：（1）
或
（2）
17．解：（1）；
（2）用树状图表示所有等可能出现的结果如下：
共有12种等可能出现的结果，其中两人都没有抽到“B．夏至”（记为事件M）的有6种，．
∴两人都没有抽到“B．夏至”的概率是．
18．解：（1）如图所示，为所求；
点的坐标分别为；
（2）如图所示，为所求；
，旋转角，
∴边AB扫过的面积为扇形的面积，
∴边AB扫过的面积为．
19．解：（1）点在反比例函数图象上，
解得反比例函数的表达式为
在反比例函数的图象上
解得点B的坐标为
点在一次函数的图象上，把点
分别代入，得解得
一次函数的表达式为．
（2）点C为直线AB与轴的交点，
．
（3）根据图象可得或者
20．解：（1）设与的函数关系式为。
把与分别代入，得
解得，
．
（2）根据题意，得：，即．
解得
答：每本纪念册的销售单价是25元．
（3）由题意，可得．
．
∴抛物线的开口向下
∵对称轴是直线∴当时，y随x的增大而增大
∴当时，w最大，（元）
答：该纪念册销售单价定为28元时，能使文具店销售该纪念册所获利润最大，最大利润是192元．
21．（1）证明：连接OP，如图
，
又∵OP为半径∴PD是的切线
（2）连接PB，如图，
为等边三角形
由（1）得
∴弧BP的长．
22．解：（1）等边三角形；
（2）如图，结论：是等边三角形．
理由：设AE交BD于点O，AC交BD于点K，连接DM．
都是等边三角形，
，
即，
，
，
，
，∴四边形ABDM是平行四边形，
，
是等边三角形．
（3）的值为60°或300°．
23．解：（1）函数的图象上存在“互反点”．
根据题意，得，解得
∴函数的图象上“互反点”的坐标为
函数的图象上存在“互反点”．
根据题意，得解得，
∴函数的图象上“互反点”的坐标为．
（2）在函数中，令
解得（负值已舍去）．
在函数中，令，解得
．
解得或；或无解．
∴b的值为4或．
（3）①根据题意，把代入得，
．
∵函数图象上的“互反点”必在直线上，
∴二次函数的图象上有且只有一个“互反点”，
也就是二次函数的图象与直线有且只有
一个交点
联立方程组整理，得．
由
解得
∴该二次函数的表达式为．
②二次函数
其图象的对称轴为直线最小值为．
当时，解得或
∴二次函数图象与x轴交点的坐标为和．
∵当时，二次函数的最小值为，最大值为0．
∴t的取值范围是．
（温馨提示：方法不同可酌情给分）题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
C
A
C
D
C
D
B
A