沪教版数学七年级上册期末复习特训06 期末历年选填压轴题（第9-11章）（2份，原卷版+解析版）

这是一份沪教版数学七年级上册期末复习特训06 期末历年选填压轴题（第9-11章）（2份，原卷版+解析版），文件包含沪教版数学七年级上册期末复习特训06期末历年选填压轴题第9-11章原卷版doc、沪教版数学七年级上册期末复习特训06期末历年选填压轴题第9-11章解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
1．（2020·上海嘉定·七年级期末）如图，在正方形ABCD中，点M是边CD的中点，那么正方形ABCD绕点M至少旋转_________度与它本身重合．
【答案】360
【分析】根据旋转对称图形的定义即可得．
【解析】点M是边CD的中点，不是正方形ABCD的中心，
正方形ABCD绕点M至少旋转360度才能与它本身重合，
故答案为：360．
【点睛】本题考查了旋转对称图形，掌握理解定义是解题关键．
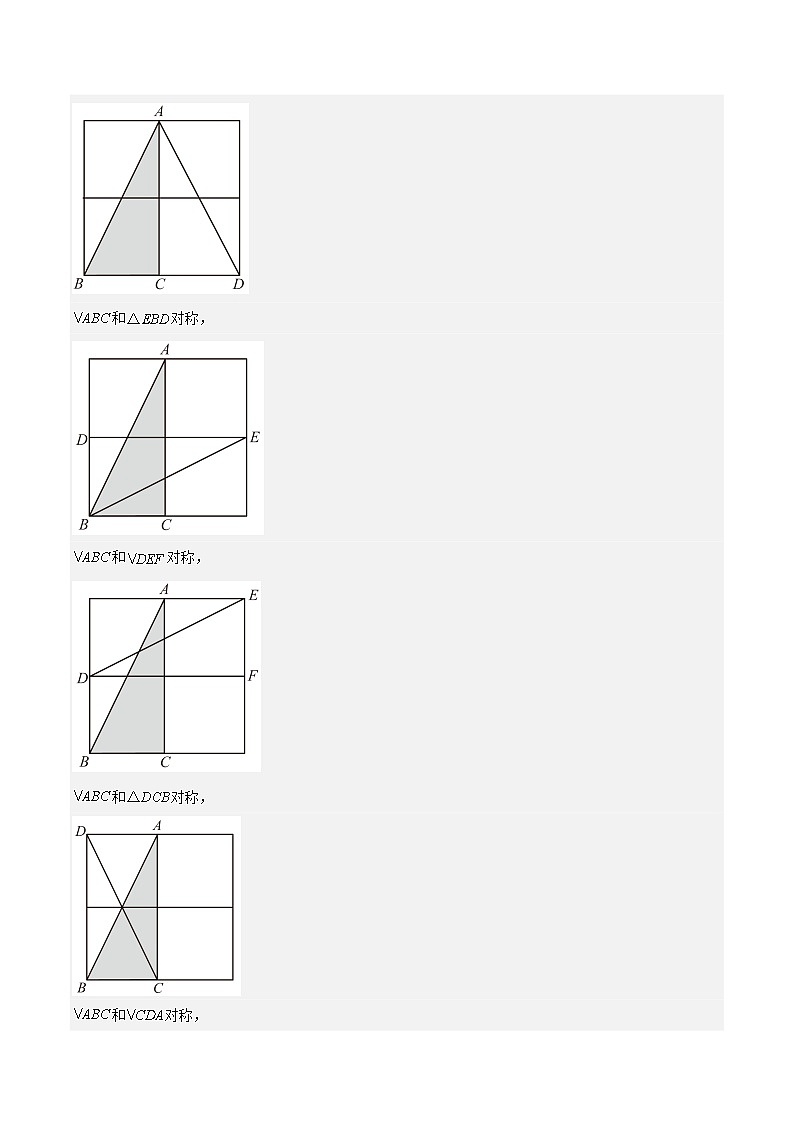
2．（2020·上海松江·七年级期末）如图，在的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的为格点三角形，在图中最多能画出______个不同的格点三角形与成轴对称．
【答案】5
【分析】画出所有与成轴对称的三角形．
【解析】解：如图所示：
和对称，
和对称，
和对称，
和对称，
和对称，
故答案是：5．
【点睛】本题考查轴对称图形，解题的关键是掌握画轴对称图形的方法．
3．（2018·上海市延安初级中学七年级期末）已知，那么的值等于___________．
【答案】
【分析】由得到a+，再将化成含的形式，再代入计算即可．
【解析】∵，
∴，即=5，
∴＝＝＝．
故答案为：．
【点睛】考查了分式的化简求值，解题关键是由得到a+和把变形成含的形式．
4．（2019·上海·上外附中七年级期末）若表示一个关于的多项式，除以整式，所得的商式和余式均为同一个多项式中的系数均为整数，则余式_____________．
【答案】x+1
【分析】由题意得，f(x)=g(x)h(x)+h(x)=h(x)[g(x)+1]，又因为=(x+1)(x2+x+2) ，这两个式子比较讨论即可得到答案.
【解析】解：由题意得，f(x)=g(x)h(x)+h(x)=h(x)[g(x)+1] ①
又∵=(x+1)(x2+x+2) ②
比较①、②可知，有下述两种情况：
（1）h(x)=x+1,g(x)+1=x2+x+2,即h(x)=x+1,g(x)=x2+x+1；
（2）h(x)= x2+x+2，g(x)+1=x+1,即h(x)= x2+x+2，g(x)=x，这里余式h(x)的次数大于除式g(x)的次数，故不合题意，
∴只有（1）成立，
故答案为x+1.
【点睛】此题主要考查了整式的除法及因式分解，正确地将进行因式分解是解决问题的关键.
5．（2020·上海市川沙中学南校七年级期末）长为5，宽为的长方形纸片（），如图那样翻折，剪下一个边长等于长方形宽度的正方形（成为第一次操作）；再把剩下的长方形如图那样翻折，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）；若在第3次操作后，剩下的图形为正方形，则的值为__________．
【答案】3或
【分析】先根据题意可知：当＜a＜20时，第一次操作后剩下的矩形的长为a、宽为5-a，第二次操作时正方形的边长为5-a，第二次操作以后剩下的矩形的两边分别为5-a、2a-5，然后分别从5-a＞2a-5与5-a＜2a-5去分析且列出一元一次方程求解即可得出正确答案．
【解析】解：由题意可知：
当＜a＜5时，
第一次操作后剩下的矩形的长为a、宽为5-a，
∴第二次操作时剪下正方形的边长为5-a，
第二次操作以后剩下的矩形的两边分别为5-a、2a-5．
此时，分两种情况：
①如果5-a＞2a-5，则a＜，
即＜a＜，
那么第三次操作时正方形的边长为2a-5．
则2a-5=(5-a)-(2a-5)，
解得a=3；
②如果5-a＜2a-5，则a＞，
即＜a＜20，
那么第三次操作时正方形的边长为5-a．
则5-a=(2a-5)-(5-a)，
解得a=．
∴当n=3时，a的值为3或．
故答案为:3或．
【点睛】本题考查的知识点有折叠的性质、矩形的性质、分类讨论思想、数形结合思想、一元一次方程的应用、一元一次不等式的应用．解题关键是 掌握数形结合思想、分类讨论思想与方程思想的应用以及注意折叠中的对应关系．
6．（2020·上海浦东新·七年级期末）已知大正方形的边长为5厘米，小正方形的边长为2厘米，起始状态如图所示. 大正方形固定不动，把小正方形以1厘米/秒的速度向右沿直线平移，设平移的时间为秒，两个正方形重叠部分的面积为平方厘米. 当时，小正方形平移的时间为_________秒．
【答案】1或6
【分析】小正方形的高不变，根据面积即可求出小正方形平移的距离．
【解析】S等于2时，重叠部分宽为2÷2=1，
①如图，小正方形平移距离为1(厘米)；时间为：1÷1=1（秒）
②如图，小正方形平移距离为5+1=6（厘米）．时间为：6÷1=6（秒）
故答案为：1或6．
【点睛】此题考查了平移的性质，要明确，平移前后图形的形状和面积不变．画出图形即可直观解答．
7．（2020·上海宝山·七年级期末）如图，已知中，、、，将沿直线BC向右平移得到，点A、B、C的对应点分别是、、，连接．如果四边形的周长为19，那么四边形的面积与的面积的比值是________．
【答案】
【分析】过点A作BC上的高，根据平移的性质可得=，且，，然后根据已知周长可得=2，从而求出，然后根据梯形的面积公式和三角形的面积公式即可求出结论．
【解析】解：过点A作BC上的高
由平移的性质可得=，且，
∴四边形为梯形
∵四边形的周长为19，
∴＋＋＋AB=19
∴＋5＋6＋＋4=19
∴2=4
∴=2
∴=2
∴=BC＋=8
∴四边形的面积与的面积的比为
故答案为：．
【点睛】此题考查的是图形的平移问题，掌握平移的性质是解题关键．
8．（2021·上海宝山·七年级期末）已知，那么的值是_____________．
【答案】9
【分析】先表示出，的值，然后代入代数式降幂计算即可．
【解析】解：∵，
∴，，
∴
=
=
=
=
=9
故答案为：9．
【点睛】本题主要考查了多项式乘多项式和求代数式的值，利用整体思想降幂是解题的关键．
9．（2021·上海浦东新·七年级期末）如图，已知直角三角形，，厘米，厘米，厘米，将沿方向平移1.5厘米，线段在平移过程中所形成图形的面积为__________平方厘米．
【答案】6
【分析】先确定BC平移后的图形是平行四边形，然后再确定平行四边的底和高，最后运用平行四边形的面积公式计算即可．
【解析】解：如图：线段在平移过程中所形成图形为平行四边形且底CE=1.5cm，高DF=AB=4cm，
所以线段在平移过程中所形成图形的面积为CE·DF=1.5×4=6cm2．
故答案为6．
【点睛】本题考查了平移的性质，根据平移的性质确定平行四边形的底和高成为解答本题的关键．
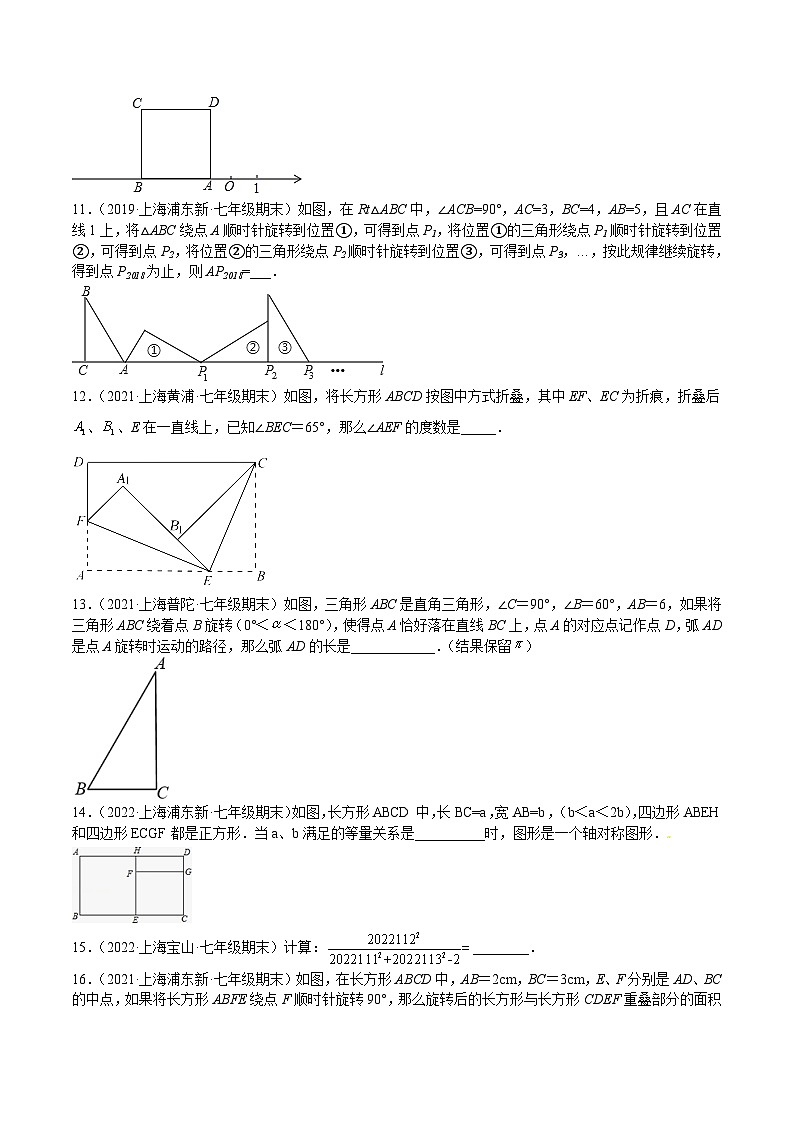
10．（2022·上海·七年级专题练习）如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为﹣1，正方形ABCD的面积为a2（a＞1）．将正方形ABCD在数轴上水平移动，移动后的正方形记为A′B′C′D′，点A、B、C、D的对应点分别为A′、B′、C′、D′，移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S．当S＝a时，数轴上点A′表示的数是_____．（用含a的代数式表示）
【答案】﹣a或a﹣2
【分析】根据正方形的面积可得边长进而可以表示点A′表示的数．
【解析】∵正方形ABCD的面积为a2（a＞1）．
∴边长为a，
当S＝a时，分两种情况：
若正方形ABCD向左平移，如图1，
A′B′＝AB＝BC＝a，
A′B＝1，
∴AA′＝AB﹣A′B＝a﹣1，
∴OA′＝OA+AA′＝1+a﹣1＝a，
∴数轴上点A′表示的数为﹣a；
如正方形ABCD向右平移，如图2，
AB′＝1，AA′＝a﹣1，
∴OA′＝（a﹣1）﹣1＝a﹣2
∴数轴上点A′表示的数为a﹣2．
综上所述，数轴上点A′表示的数为﹣a或a﹣2．
【点睛】本题考查了实数与数轴，解决本题的关键是根据正方形平移后用代数式表示线段的长度．
11．（2019·上海浦东新·七年级期末）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AB=5，且AC在直线1上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，…，按此规律继续旋转，得到点P2018为止，则AP2018=___．
【答案】8073
【分析】观察不难发现，每旋转3次为一个循环组依次循环，用2018除以3求出循环组数，然后列式计算即可得解．
【解析】∵Rt△ABC中，∠ACB=90°，AC=3，BC=4，AB=5，
∴将△ABC绕点A顺时针旋转到①，可得到点P1，此时AP1=5；
将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=5+4=9；
将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=5+4+3=12；
又∵2018÷3=672…2，
∴AP2018=672×12+（5+4）=8064+9=8073．
故答案为8073．
【点睛】本题考查了旋转的性质及图形的规律问题，得到AP的长度依次增加5，4，3，且三次一循环是解题的关键．
12．（2021·上海黄浦·七年级期末）如图，将长方形ABCD按图中方式折叠，其中EF、EC为折痕，折叠后、、E在一直线上，已知∠BEC＝65°，那么∠AEF的度数是_____．
【答案】25°
【分析】利用翻折变换的性质即可解决．
【解析】解：由折叠可知，∠EF＝∠AEF，∠EC＝∠BEC＝65°，
∵∠EF+∠AEF+∠EC+∠BEC＝180°，
∴∠EF+∠AEF＝50°，
∴∠AEF＝25°，
故答案为：25°．
【点睛】本题考查了折叠的性质，熟练掌握折叠的性质是解题的关键．
13．（2021·上海普陀·七年级期末）如图，三角形ABC是直角三角形，∠C＝90°，∠B＝60°，AB＝6，如果将三角形ABC绕着点B旋转（0°＜＜180°），使得点A恰好落在直线BC上，点A的对应点记作点D，弧AD是点A旋转时运动的路径，那么弧AD的长是____________．（结果保留）
【答案】2或4
【分析】分当△ABC绕点B顺时针旋转60°时，点A与重合，当△ABC绕点B逆时针旋转120°时，点A与重合，两种情况讨论求解即可．
【解析】解：如图所示，
∵∠ABC=60°，
∴，
∴当△ABC绕点B顺时针旋转60°时，点A与重合，当△ABC绕点B逆时针旋转120°时，点A与重合，
∴，，
故答案为：或．
【点睛】本题主要考查了求弧长，解题的关键在于能够熟练掌握弧长公式．
14．（2022·上海浦东新·七年级期末）如图，长方形ABCD中，长BC=a，宽AB=b，（b＜a＜2b），四边形ABEH和四边形ECGF都是正方形．当a、b满足的等量关系是__________时，图形是一个轴对称图形．
【答案】
【解析】∵当图形是一个轴对称图形,则必须满足DG=CG=EC,长BC=a,宽AB=b,(b