




所属成套资源:2025年中考数学一轮复习讲义(含练习)
第07讲 一元二次方程(讲义)-2025年中考数学一轮复习讲义(含练习)
展开
这是一份第07讲 一元二次方程(讲义)-2025年中考数学一轮复习讲义(含练习),文件包含第07讲一元二次方程讲义教师版docx、第07讲一元二次方程讲义学生版docx等2份试卷配套教学资源,其中试卷共106页, 欢迎下载使用。
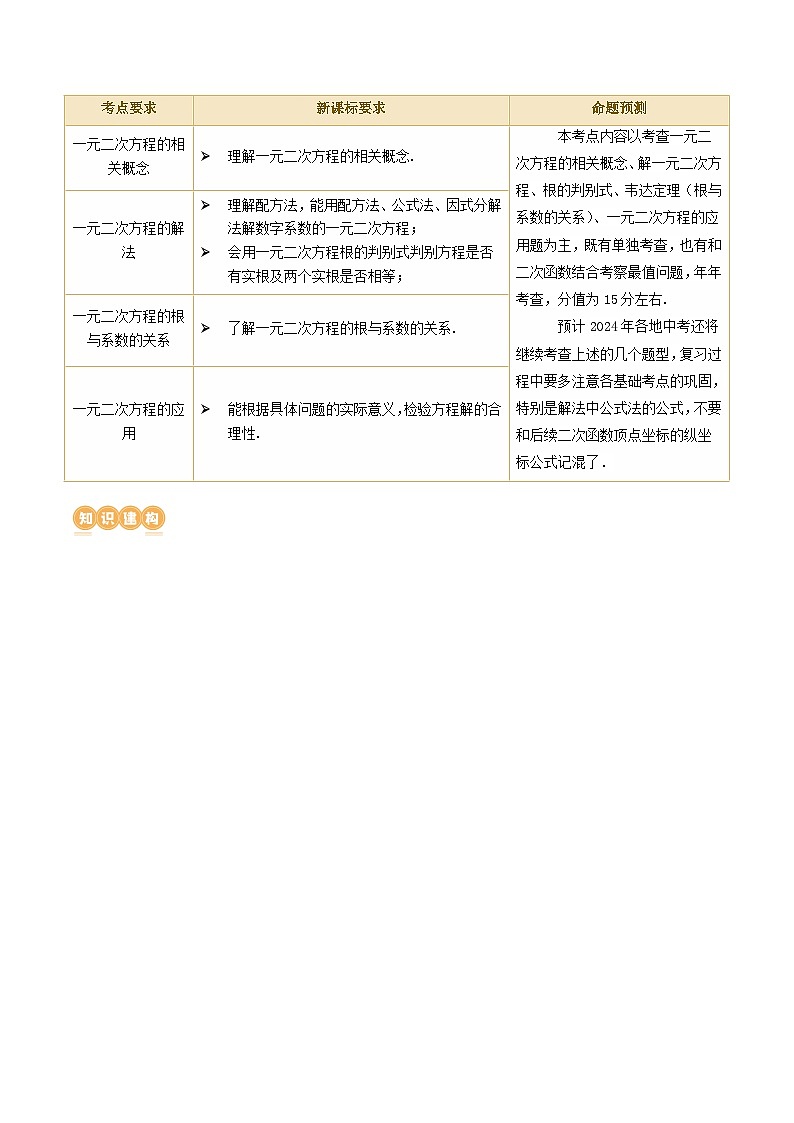
一、考情分析
二、知识建构 TOC \ "1-3" \n \h \z \u \l "_Tc152160052"
\l "_Tc152160053" 考点一 一元二次方程的相关概念
\l "_Tc152160054" 题型01 识别一元二次方程
\l "_Tc152160055" 题型02 由一元二次方程的概念求参数的值
\l "_Tc152160056" 题型03 一元二次方程的一般式
\l "_Tc152160057" 题型04 由一元二次方程的解求参数的值
\l "_Tc152160058" 题型05 由一元二次方程的解求代数式的值
\l "_Tc152160059" 题型06 已知一元二次方程的一个根,求另一个根
\l "_Tc152160060" 考点二 解一元二次方程
\l "_Tc152160061" 题型01 用直接开平方法解一元二次方程
\l "_Tc152160062" 题型02 利用配方法解一元二次方程
\l "_Tc152160063" 题型03 利用因式分解法解一元二次方程
\l "_Tc152160064" 题型04 利用公式法解一元二次方程
\l "_Tc152160065" 题型05 利用换元法解一元二次方程
\l "_Tc152160066" 题型06 选用合适的方法解一元二次方程
\l "_Tc152160067" 题型07 错看或错解一元二次方程问题
\l "_Tc152160068" 题型08 配方法的应用
\l "_Tc152160069" 题型09 判断不含字母的一元二次方程的根的情况
\l "_Tc152160070" 题型10 判断含字母的一元二次方程根的情况
\l "_Tc152160071" 题型11 由方程根的情况确定字母的值或取值范围
\l "_Tc152160072" 题型12 应用根的判别式证明方程根的情况
\l "_Tc152160073" 题型13 应用根的判别式求代数式的取值范围
\l "_Tc152160074" 题型14 与根的判别式有关的新定义问题
\l "_Tc152160075" 考点三 一元二次方程根与系数的关系
\l "_Tc152160076" 题型01 由根与系数的关系直接求代数式的值
\l "_Tc152160077" 题型02 由根与系数的关系和方程的解通过代换求代数式的值
\l "_Tc152160078" 题型03 由根与系数的关系和方程的解通过降次求代数式的值
\l "_Tc152160079" 题型04 由方程两根满足关系求字母或代数式的值
\l "_Tc152160080" 题型05 不解方程由根与系数的关系判断根的正负
\l "_Tc152160081" 题型06 由方程两根的不等关系确定字母系数的取值范围
\l "_Tc152160082" 题型07 与根与系数有关的新定义问题
\l "_Tc152160083" 题型08 构造一元二次方程求代数式的值
\l "_Tc152160084" 题型09 根与系数的关系和根的判别式的综合应用
\l "_Tc152160085" 考点四 一元二次方程的应用
\l "_Tc152160086" 题型01 分裂(传播)问题
\l "_Tc152160087" 题型02 碰面(循环)问题
\l "_Tc152160088" 题型03 增长率问题
\l "_Tc152160089" 题型04 营销问题
\l "_Tc152160090" 题型05 工程问题
\l "_Tc152160091" 题型06 行程问题
\l "_Tc152160092" 题型07 与图形有有关的问题
考点一 一元二次方程的相关概念
1. 如果明确了ax2+bx+c=0是一元二次方程,就隐含了a≠0这个条件(当a=0时,不含有二次项,即不是一元二次方程).
2. 一元二次方程必须具备三个条件:
①必须是整式方程;②必须只含有一个未知数;③所含未知数的最高次数是2.
3. 在判断一个方程是不是一元二次方程时,要先化成一般形式,再判断.
4. 二次项系数、一次项系数和常数项都是在一般形式下定义的.所以在确定一元二次方程各项的系数时,应先将方程化为一般形式.
5. 一元二次方程的解,要么无解,有解必有两个,所以最后方程的解一定要写明x1,x2.
题型01 识别一元二次方程
【例1】(2023·江西抚州·金溪一中校考模拟预测)下列方程是一元二次方程的是( )
A.x2-1=0B.2x+y=1C.x+1x=3D.4x+5=6x
【变式1-1】(2023·四川成都·一模)下列方程是一元二次方程的是( )
A.x2+x-y=0B.ax2+2x-3=0
C.x2+2x+5=x(x-1)D.x2-1=0
题型02 由一元二次方程的概念求参数的值
【例2】(2023 南阳市一模)关于x的方程m+1xm+1-mx+6=0是一元二次方程,则m的值是( )
A.-1B.3C.1D.1或-1
【变式2-1】(2022上·辽宁沈阳·九年级期中)方程(m-2)xm2-2+(5+m)x+3=0是关于x的一元二次方程,则m= .
题型03 一元二次方程的一般式
【例3】(2022上·河南郑州·九年级郑州外国语中学校考期中)将一元二次方程3x2=5x-1写成一般形式,下列等式正确的是( )
A.3x2-5x-1=0B.3x2+5x-1=0
C.3x2-5x+1=0D.3x2+5x+1=0
【变式3-1】(2023·广东东莞·东莞市东华初级中学校考模拟预测)将方程4x2+8x=25化成ax2+bx+c=0的形式,则a,b,c的值分别为( )
A.4,8,25B.4,2,-25C.4,8,-25 D.1,2,25
【变式3-2】.(2021上·山西晋中·九年级阶段练习)若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为 .
【变式3-3】(2023集贤县·九年级期中)已知关于x的一元二次方程a-1x2+x+a2-1=0的常数项是0,则a的值为( )
A.1B.-1C.1或-1D.12
题型04 由一元二次方程的解求参数的值
【例4】(2022·广东·中考真题)若x=1是方程x2-2x+a=0的根,则a= .
【变式4-1】(2021·湖南长沙·中考真题)若关于x的方程x2-kx-12=0的一个根为3,则k的值为 .
利用方程根的概念将方程的根代入原方程再解方程就可以求出参数的值,同时还要注意限制参数取值的其他隐含条件.
题型05 由一元二次方程的解求代数式的值
【例5】(2023·甘肃陇南·一模)关于x的一元二次方程2xa-2+m=4的解为x=1,则a+m的值为( )
A.9B.8C.6D.4
【变式5-1】(2023·北京海淀·校考模拟预测)如果x=-1是方程x2+mx+n=0的一个根,那么m、n的大小关系是( )
A.m>nB.m=nC.m0;
2)有两个相等的实数根时, Δ=0;
3)没有实数根时, Δb,则2a+b的值为 .
【变式1-2】(2023·齐齐哈尔市模拟)解关于x的方程: 42x-52=93x-12.
题型02 利用配方法解一元二次方程
【例2】(2022·甘肃武威·中考真题)用配方法解方程x2-2x=2时,配方后正确的是( )
A.x+12=3B.x+12=6C.x-12=3D.x-12=6
【变式2-1】(2022·山东聊城·中考真题)用配方法解一元二次方程3x2+6x-1=0时,将它化为x+a2=b的形式,则a+b的值为( )
A.103B.73C.2D.43
【变式2-2】(2023·山西大同·校联考模拟预测)将方程2x2-12x+1=0配方成x-m2=n的形式,下列配方结果正确的是( )
A.x+32=17B.x+32=172C.x-32=17D.x-32=172
【变式2-3】(2022松原市三模)用配方法解方程x2-4x-3=0,配方得(x+m)2=7,常数m的值是 .
题型03 利用因式分解法解一元二次方程
【例3】(2022·广西梧州·中考真题)一元二次方程x-2x+7=0的根是 .
【变式3-1】(2023惠阳区模拟预测)三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的根,则该三角形的周长为 .
【变式3-2】(2023·江苏南京·二模)解方程:xx-6=-4x-6.
题型04 利用公式法解一元二次方程
【例4】(2023·甘肃陇南·一模)用公式法解方程x2-4x-11=0时,Δ=( )
A.-43B.-28C.45D.60
【变式4-1】(2023·江苏无锡·一模)方程x2-3x=1的解是 .
【变式4-2】(2023·内蒙古呼伦贝尔·校考一模)方程x2+2x-2=0的解是 .
【变式4-3】(2023长岭县模拟)一元二次方程x2-3x+2=0根的判别式的值为 .
题型05 利用换元法解一元二次方程
【例5】(2023·浙江宁波·校考一模)已知a2+b22-a2-b2-6=0,求a2+b2的值为 .
【变式5-1】(2023罗湖区模拟预测)若x2+y2+3x2+y2-3=16,则x2+y2= .
【变式5-2】我们知道方程x2+2x-3=0的解是x1=1,x2=-3,现给出另一个方程(2x+3)2+2(2x+3)-3=0,它的解是( )
A.x1=1,x2=3B.x1=1,x2=-3
C.x1=-1,x2=3 D.x1=-1,x2=-3
【变式5-3】(2023·四川绵阳·二模)二次函数y=ax2+bx+c的部分对应值如列表所示:则一元二次方程a(2x-1)2+b2x-1+c=7的解为 .
题型06 选用合适的方法解一元二次方程
【例6】(2023西安高新一中一模)解方程:x2-4x-5=0.
【变式6-1】(2023·广东广州·一模)解方程(x-2)2=4.
【变式6-2】(2022秋·江苏镇江·九年级统考期中)解下列方程
(1)9x2-x-12=0
(2)x2-4x-1=0
(3)2x2-x-3=0
题型07 错看或错解一元二次方程问题
【例7】(2022·浙江温州·一模)关于x的方程x(x﹣1)=3(x﹣1),下列解法完全正确的是( )
A.AB.BC.CD.D
【变式7-1】下面是小明同学的错题本的一部分,请你仔细阅读,帮助他补充完整.
解方程: x-32=4x2
解: x-3=2x …第一步
x-2x=3⋯ 第二步
x=-3⋯ 第三步
(1)提示:第 步开始出现错误;
(2)改正:
【变式7-2】(2021·浙江嘉兴·中考真题)小敏与小霞两位同学解方程3x-3=x-32的过程如下框:
你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.
【变式7-3】(2023·山西晋中·模拟预测)(1)计算:sin45°+tan45°-2cs60°.
(2)下面是小明同学解方程的过程,请认真阅读并完成相应的任务.
任务一:
①填空:上述材料中小明同学解一元二次方程的数学方法是 ,依据的一个数学公式是 ;第 步开始出现错误;
任务二:
②请你直接写出该方程的正确解.
【变式7-4】(2023上·北京东城·九年级期末)下面是小聪同学用配方法解方程:2x2-4x-p=0 p>0的过程,请仔细阅读后,解答下面的问题.
2x2-4x-p=0
解:移项,得:2x2-4x=p.①
二次项系数化为1,得:x2-2x=p2.②
配方,得x2-2x+1=p2.③
即(x-1)2=p2.
∵p>0,
∴x-1=±p2.④
∴x1=1+2p2,x1=1-2p2.⑤
(1)第②步二次项系数化为1的依据是什么?
(2)整个解答过程是否正确?若不正确,说出从第几步开始出现的错误,并直接写出此方程的解.
题型08 配方法的应用
【例8】(2023上·江西九江·九年级阶段练习)【课本再现】
【尝试运用】
(1)解一元二次方程x2-4x-2=0,配方后可变形为( )
A.x-42=8 B.x-42=6 C.x-22=2 D.x-22=6
(2)利用配方法求-x2-6x+5的最值.
【拓展应用】
(3)已知方程x2+y2+2x-4y+5=0,求x-2y的值.
【变式8-1】(2023上·广东深圳·九年级校考阶段练习)配方法在代数式求值、解方程、求最值问题……中都有着广泛的应用.
例如:若代数式M=a2-2ab+2b2-2b+2,
利用配方法求M的最小值:M=a2-2ab+2b2-2b+2
=a2-2ab+b2+b2-2b+1
=(a-b)2+(b-1)2+1
∵(a-b)2≥0,(b-1)2≥0,
∴当a=b=1时,代数式M有最小值为1.
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a2+6a+_________;
(2)若代数式M=a2+4a+6,求M的最小值;
(3)已知a2+2b2+c2-2ab-2b-4c+5=0,求代数式a+b+c的值.
题型09 判断不含字母的一元二次方程的根的情况
【例9】(2022·山东滨州·中考真题)一元二次方程2x2-5x+6=0的根的情况为( )
A.无实数根B.有两个不等的实数根
C.有两个相等的实数根D.不能判定
【变式9-1】(2022·辽宁抚顺·中考真题)下列一元二次方程无实数根的是( )
A.x2+x-2=0B.x2-2x=0
C.x2+x+5=0D.x2-2x+1=0
【变式9-2】(2020·安徽·中考真题)下列方程中,有两个相等实数根的是( )
A.x2+1=2xB.x2+1=0
C.x2-2x=3D.x2-2x=0
【变式9-3】(2022·江苏扬州·中考真题)请填写一个常数,使得关于x的方程x2-2x+ =0有两个不相等的实数根.
若一元二次方程ax2+bx+c=0(a≠0)中ac-1且a≠0C.a≥-1且a≠0D.a>-1
【变式11-2】(2022·江苏淮安·中考真题)若关于x的一元二次方程x2-2x-k=0没有实数根,则k的值可以是( )
A.-2B.-1C.0D.1
【变式11-3】(2023绵阳市模拟)关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是 .
题型12 应用根的判别式证明方程根的情况
【例12】(2022上·福建福州·九年级福建省福州铜盘中学校考阶段练习)已知关于x的一元二次方程x2+mx+m-1=0.
(1)求证:方程总有两个实数根;
(2)如果方程有一个根为正数,求m的取值范围.
【变式12-1】(2022·湖北十堰·中考真题)已知关于x的一元二次方程x2-2x-3m2=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根分别为α,β,且α+2β=5,求m的值.
【变式12-2】(2022·北京朝阳·一模)已知关于x的一元二次方程x2-ax+a-1=0.
(1)求证:该方程总有两个实数根;
(2)若该方程的两个实数根都是整数,且其中一个根是另一个根的2倍,求a的值.
【变式12-3】(2023·广东江门·二模)已知关于x的方程x2+3k-2x-6k=0.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰三角形△ABC的一边a=6,另两边长b、c恰好是这个方程的两个根,求△ABC的周长.
题型13 应用根的判别式求代数式的取值范围
【例13】(2023·河南信阳·校考三模)关于x的一元二次方程m-3x2-2x+1=0有实数根,则m的取值范围是( )
A.m4 C. m≥4D.m≤4且m≠3
【变式13-1】(2022株洲市二中二模)若关于x的方程kx2-3x-94=0有实数根,则实数k的取值范围是( )
A.k=0 B.k≥-1且k≠0C.k≥-1 D.k>-1
【变式13-2】(2023·湖北襄阳·模拟预测)已知关于x的一元二次方程x2-6x+2m-1=0有x1,x2两实数根.
(1)求m的取值范围;
(2)是否存在实数m,满足x1-1x2-1=-6m-7?若存在,求出实数m的值;若不存在,请说明理由.
【变式13-3】(2023·湖北孝感·校考模拟预测)已知关于x的一元二次方程x2+3x+2k-1=0有两个实数根x1,x2
(1)求k的取值范围;
(2)若x12-x22=35,求k的值.
【变式13-4】(2023·浙江·模拟预测)已知三个关于x的方程x2-x+m=0,(m-1)x2+2x+1=0和(m-2)x2+2x-1=0.若其中至少有两个方程有实根,求实数m的取值范围.
题型14 与根的判别式有关的新定义问题
【例14】(2020·湖北荆州·中考真题)定义新运算a*b,对于任意实数a,b满足a*b=a+ba-b-1,其中等式右边是通常的加法、减法、乘法运算,例如4*3=(4+3)(4-3)-1=7-1=6,若x*k=x(k为实数) 是关于x的方程,则它的根的情况是( )
A.有一个实根B.有两个不相等的实数根
C.有两个相等的实数根D.没有实数根
【变式14-1】(2022·内蒙古·中考真题)对于实数a,b定义运算“⊗”为a⊗b=b2-ab,例如3⊗2=22-3×2=-2,则关于x的方程(k-3) ⊗x=k-1的根的情况,下列说法正确的是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.无法确定
【变式14-2】(2020·河南·中考真题)定义运算:m☆n=mn2-mn-1.例如:4☆2=4×22-4×2-1=7.则方程1☆x=0的根的情况为( )
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.只有一个实数根
考点三 一元二次方程根与系数的关系
若一元二次方程ax2+bx+c=0(a≠0 QUOTE ≠0,Δ≥0 )的两个根是x1和x2,则x1,x2与方程的系数a,b,c之间有如下关系:x1+x2=-ba; x1•x2=ca
【扩展】用根与系数的关系求值时的常见转化:
已知一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2
1)平方和 x12+x22= (x1+x2)2-2x1x2
2)倒数和 1x1 + 1x2 =x1+x2x1x2
3)差的绝对值 | x1 - x2 |=(x1-x2)2=(x1+x2)2-4x1x2
4) x1x2+x2x1 = x12+x22x1x2=(x1+x2)2-2x1x2x1x2
5) (x1+1)(x2+1)=x1x2+(x1+x2)+1
1. 如果方程x2+px+q=0的两个根为x1,x2,那么x1+x2=-p, x1•x2=q.
2. 以两个数x1,x2为根的一元二次方程(二次项系数为1)是x2 -(x1+x2)x+x1•x2=0.
3. 运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定 a、b、c的值.
4. 一元二次方程根与系数关系的使用条件:a≠0且△≥0.
题型01 由根与系数的关系直接求代数式的值
【例1】(2022·贵州黔东南·中考真题)已知关于x的一元二次方程x2-2x-a=0的两根分别记为x1,x2,若x1=-1,则a-x12-x22的值为( )
A.7B.-7C.6D.-6
【变式1-1】(2023·湖北武汉·模拟预测)已知m,n是一元二次方程x2+3x-2=0的两根,则2m-n-m+3nm2-n2的值是( )
A.-3B.-2C.-13D.-12
【变式1-2】(2023汉寿县一模)已知a、b是一元二次方程x2+5x+3=0的两个根,则aba+bab的值是( )
A.-23B.-32C.32D.23
【变式1-3】(2022·湖南娄底·中考真题)已知实数x1,x2是方程x2+x-1=0的两根,则x1x2= .
【变式1-4】(2021·湖北黄冈·一模)已知一元二次方程x2﹣3x+1=0有两个实数根x1,x2,则x1+x2﹣x1x2的值等于 .
【变式1-5】(2021·湖北孝感·一模)已知方程x2-4x-1=0的两根为x1,x2,则1-x11-x2= .
求含有两根的代数式的值:将所求代数式通过因式分解或配方等恒等变形,变形为含有两根和与两根积的式子,再代入由一元二次方程根与系数关系得到的值,求出结果.
题型02 由根与系数的关系和方程的解通过代换求代数式的值
【例2】(2023潜江市模拟)若α、β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为( )
A.-13B.12C.14D.15
【变式2-1】(2021·江苏南通·中考真题)若m,n是一元二次方程x2+3x-1=0的两个实数根,则m3+m2n3m-1的值为 .
【变式2-2】(2021·四川成都·中考真题)若m,n是一元二次方程x2+2x-1=0的两个实数根,则m2+4m+2n的值是 .
题型03 由根与系数的关系和方程的解通过降次求代数式的值
【例3】(2022·内蒙古呼和浩特·中考真题)已知x1,x2是方程x2-x-2022=0的两个实数根,则代数式x13-2022x1+x22的值是( )
A.4045B.4044C.2022D.1
【变式3-1】(2023连云港市检测)已知α、β是方程x2﹣2x﹣4=0的两个实数根,则α3+8β+6的值为( )
A.﹣1B.2C.22D.30
【变式3-2】(2021上·湖北武汉·九年级武汉市武珞路中学校考期中)已知a,b是方程x2-x-1=0的两根,则代数式2a3+5a+3b3+3b+1的值是( )
A.19B.20C.14D.15
【变式3-3】(2021·湖北武汉·中考真题)已知a,b是方程x2-3x-5=0的两根,则代数式2a3-6a2+b2+7b+1的值是( )
A.-25B.-24C.35D.36
【变式3-4】已知α、β是方程x2+x-1=0的两根,则α4β-β3+5的值是( )
A.7B.8C.9D.10
【变式3-5】(2020·浙江杭州·九年级专题练习)已知α,β是方程x2+2x-1=0的两根,则α3+5β+10的值为 .
题型04 由方程两根满足关系求字母或代数式的值
【例4】(2022·四川泸州·中考真题)已知关于x的方程x2-2m-1x+m2=0的两实数根为x1,x2,若x1+1x2+1=3,则m的值为( )
A.-3B.-1C.-3或3D.-1或3
【变式4-1】(2022·湖北武汉·校联考模拟预测)已知关于x的一元二次方程x2+2mx+m2-m=0的两实数根为x1,x2,且满足x1x2=2,则x1+x2的值为( )
A.4B.-4C.4或-2D.-4或2
【变式4-2】(2022·广东佛山·二模)若a、b是关于x的一元二次方程x2-2kx+4k=0的两个实数根,且a2+b2=12,则k的值是( )
A.-1B.3C.-1或3D.-3或1
【变式4-3】(2019·广东广州·中考真题)关于x的一元二次方程x2-(k-1)x-k+2=0有两个实数根x1,x2,x1-x2+2(x1-x2-2)+2x1x2 =-3,则k的值( )
A.0或2B.-2或2C.-2D.2
【变式4-4】(2022·四川内江·中考真题)已知x1、x2是关于x的方程x2﹣2x+k﹣1=0的两实数根,且x2x1+x1x2=x12+2x2﹣1,则k的值为 .
【变式4-5】(2022·四川巴中·中考真题)α、β是关于x的方程x2-x+k-1=0的两个实数根,且α2-2α-β=4,则k的值为 .
题型05 不解方程由根与系数的关系判断根的正负
【例5】(2020·江苏南京·中考真题)关于x的方程(x-1)(x+2)=ρ2(ρ为常数)根的情况下,下列结论中正确的是( )
A.两个正根B.两个负根
C.一个正根,一个负根D.无实数根
【变式5-1】(2023秦淮区9年纪月考)已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )
A.x1≠x2B.x1+x2>0C.x1•x2>0D.x1<0,x2<0
【变式5-2】(2021·江苏南京·一模)关于x的方程3x2-7x+4=0的根的情况,下列结论中正确的是( )
A.两个正根B.两个负根
C.一个正根,一个负根D.无实数根
【变式5-3】关于x的方程x-2x+1=p2(p为常数)根的情况,下列结论中正确的是( )
A.有两个相异正根B.有两个相异负根C.有一个正根和一个负根D.无实数根
题型06 由方程两根的不等关系确定字母系数的取值范围
【例6】(2023·湖北省直辖县级单位·校联考二模)已知关于x的一元二次方程x2-6x+(2m+1)=0的两个实数根为x1、x2,且2x1x2+x1+x2≥20,则m的取值范围是( )
A.m≥3B.m≤-4C.3≤m≤4D.-3≤m≤4
【变式6-1】(2023·四川绵阳·三模)已知关于x的方程4x2-k+5x-k-9=0有两个不相等的实数根x1,x2,且x1=-1,0
相关试卷
这是一份第06讲 分式方程(讲义)-2025年中考数学一轮复习讲义(含练习),文件包含第06讲分式方程讲义教师版docx、第06讲分式方程讲义学生版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
这是一份第01讲 实数(讲义)-2025年中考数学一轮复习讲义(含练习),文件包含第01讲实数讲义教师版docx、第01讲实数讲义学生版docx等2份试卷配套教学资源,其中试卷共77页, 欢迎下载使用。
这是一份第07讲 一元二次方程(讲义)2024年中考数学一轮复习(讲义+练习)(全国通用),文件包含第07讲一元二次方程讲义原卷版docx、第07讲一元二次方程讲义解析版docx等2份试卷配套教学资源,其中试卷共106页, 欢迎下载使用。









