初中数学人教版（2024）九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆课后复习题

这是一份初中数学人教版（2024）九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆课后复习题，共7页。试卷主要包含了动点定长模型，定边对直角模型，定边对定角模型，四点共圆模型等内容，欢迎下载使用。
辅助圆（隐圆）是各地中考选择题和填空题、甚至解答题中的常考题，题目常以动态问题出现，有点、线的运动，或者图形的折叠、旋转等．辅助圆（隐圆）常见的有以下四种形式，动点定长、定边对直角、定边对定角、四点共圆，上述四种动态问题的轨迹是圆．题目具体表现为折叠问题、旋转问题、角度不变问题等，此类问题综合性强，隐蔽性强,很容易造成同学们的丢分．本课时就辅助圆模型进行专项训练，帮助同学们熟练掌握．
1、动点定长模型（圆的定义）
如图1，若P为动点，但AB=AC=AP，则B，C，P三点共圆，A为圆心，AB长为半径．
圆的定义：平面内到定点的距离等于定值的所有点构成的集合．
寻找隐圆技巧：若动点到平面内某定点的距离始终为定值，则其轨迹是圆或圆弧．

图1 图2
2、定边对直角模型（直角对直径）
如图2，固定线段AB所对动角∠C恒为90°，则A，B，C三点共圆，AB为直径．
寻找隐圆技巧：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．
3、定边对定角模型（定弦定角模型）
如图3，固定线段AB所对同侧动角∠P=∠C，则A，B，C，P四点共圆．

图3 图4
根据圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角都相等．
寻找隐圆技巧：AB为定值，∠P为定角，则P点轨迹是一个圆．
4、四点共圆模型（对角互补模型与等弦对等角）
如图4，若平面上A，B，C，D四个点满足，则A，B，C，D四点共圆．
寻找隐圆技巧：（1）四边形对角互补；（2）四边形外角等于内对角．
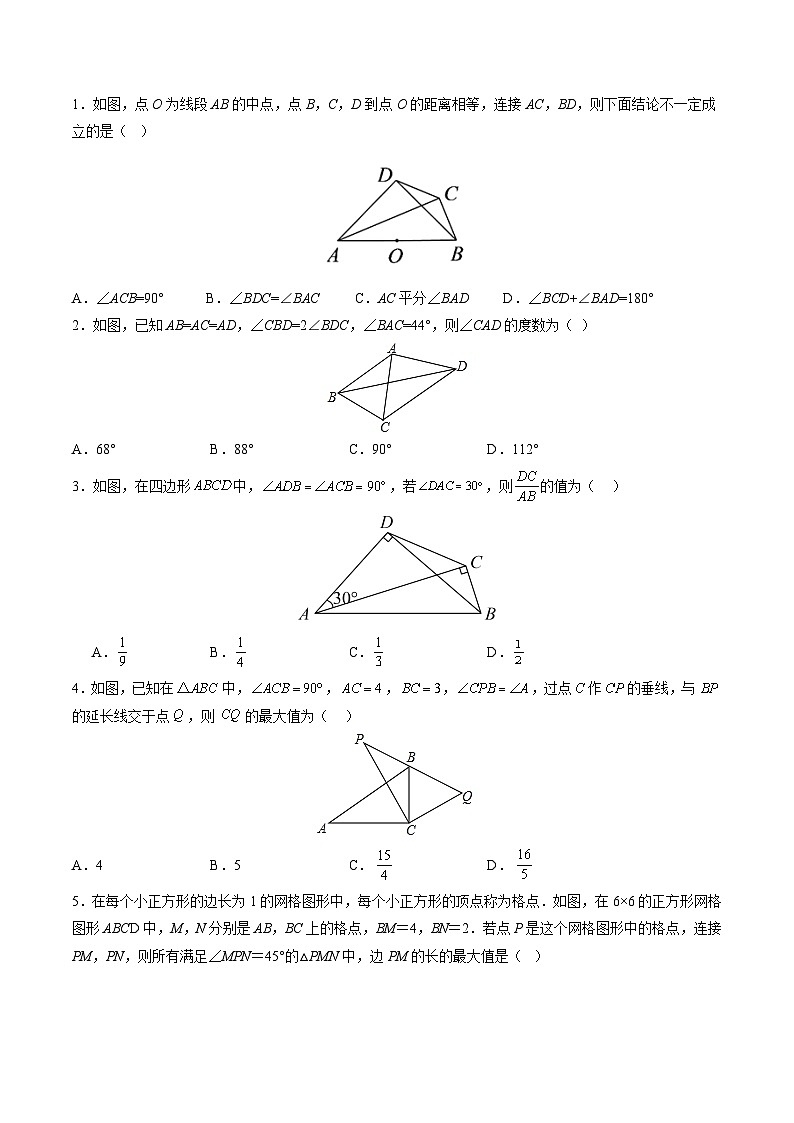
1．如图，点O为线段AB的中点，点B，C，D到点O的距离相等，连接AC，BD，则下面结论不一定成立的是（ ）
A．∠ACB=90° B．∠BDC=∠BAC C．AC平分∠BAD D．∠BCD+∠BAD=180°
2．如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（ ）
A．68°B．88°C．90°D．112°
3．如图，在四边形中，，若，则的值为（ ）
A．B．C．D．
4．如图，已知在中，，，，，过点作的垂线，与的延长线交于点，则的最大值为（ ）
A．4B．5C．D．
5．在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM＝4，BN＝2．若点P是这个网格图形中的格点，连接PM，PN，则所有满足∠MPN＝45°的△PMN中，边PM的长的最大值是（ ）
A．B．6C．D．
6．如图，在△ABC中，∠C＝90°，AC＝8，AB＝10，D是AC上一点，且CD＝3，E是BC边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为_______．
7．如图，在中，，，，是平面内一动点，且，取的中点，连接，则线段的最大值为 ．
8．如图，是和的公共斜边，AC=BC，，E是的中点，连接DE，CE，CD，那么___________________．
9．如图，在中，，，若D是与点C在直线异侧的一个动点，且，则的最大值为__________________．

10．如图，四边形为矩形，，．点P是线段上一动点，点M为线段上一点，，则的最小值为（ ）
A．B．C．D．
11．如图，在中，，，，点P为平面内一点，且，过C作交PB的延长线于点Q，则CQ的最大值为（ ）
A．B．C．D．
12．如图，在边长为1的菱形中，，动点E在边上（与点A、B均不重合），点F在对角线上，与相交于点G，连接，若，则下列结论错误的是（ ）
A．B．C．D．的最小值为
13．如图，在中，，为的中点，平分交于点，，分别与，交于点，，连接，，则的值为 ；若，则的值为 ．
14．如图，是的直径，，C为的三等分点（更靠近A点），点P是上一个动点，取弦的中点D，则线段的最大值为__________．
15．如图，△ABC为等边三角形，AB＝2，若P为△ABC内一动点，且满足∠PAB＝∠ACP，则点P运动的路径长为_________．
16．定义：三角形一个内角的平分线与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．
（1）如图1，∠E是△ABC中∠A的遥望角．
①若∠A＝40°，∠E的度数是 ；
②求∠E与∠A的数量关系，并说明理由．
（2）如图2，在四边形ABCD中，∠ABC＝∠ADC＝90°，点E在BD的延长线上，连接CE，若∠BEC是△ABC中∠BAC的遥望角，求证：DA＝DE．
17．（1）【学习心得】小刚同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．
例如：如图1，在中，，D是外一点，且，求的度数．若以点A为圆心，AB为半径作辅助圆，则点C、D必在上，是的圆心角，而是圆周角，从而可容易得到 ．
（2）【问题解决】如图2，在四边形中，，求的数．小刚同学认为用添加辅助圆的方法，可以使问题快速解决，他是这样思考的：的外接圆就是以的中点为圆心，长为半径的圆；的外接圆也是以的中点为圆心，长为半径的圆．这样A，B，C，D四点在同一个圆上，进而可以利用圆周角的性质求出的度数，请运用小刚的思路解决这个问题．
（3）【问题拓展】如图3，在中，，是边上的高，且，求的长．
18．（2023·淮安·中考真题）如图，在四边形中，为内部的任一条射线（不等于），点关于的对称点为，直线与交于点，连接，则面积的最大值是 ．
19．（2023·湖北随州·中考真题）如图，在矩形中，，M是边上一动点（不含端点），将沿直线对折，得到．当射线交线段于点P时，连接，则的面积为 ，的最大值为 ．
20．（2023·辽宁·中考真题）如图，在矩形中，，，点M为的中点，E是上的一点，连接，作点B关于直线的对称点，连接并延长交于点F．当最大时，点到的距离是 ．