初中数学浙教版（2024）九年级上册3.3 垂径定理教案设计

这是一份初中数学浙教版（2024）九年级上册3.3 垂径定理教案设计，共5页。教案主要包含了复习提问，创设情境，引入新课，揭示课题，讲解新课，探求新知，目标训练,及时反馈，总结回顾，反思内化等内容，欢迎下载使用。
1.经历探索垂径定理的过程.
2.探索并掌握垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧.
3.会运用垂径定理解决一些简单的几何问题.
教学重点
本节教学的重点是垂径定理.
教学难点
垂径定理的导出过程有一定难度，是本节教学的难点.
一、复习提问，创设情境
AB=AC
1.等腰三角形是轴对称图形吗?
答：是
2.它的对称轴是什么？
答：底边上的高（顶角的角平分线或底边上的中线）所在的直线；
3.如果把等腰三角形沿它的对称轴折叠，你能发现什么？
答：①∠BAD=∠CAD；
②BD=CD；
追问：其实刚才得到的性质总结起来，就是等腰三角形的性质？
答：等腰三角形三线合一.
二、引入新课，揭示课题
(1).基础铺设
1.圆是轴对称图形吗?
答：是
2.它有几条对称轴？哪无数条？
答：无数条，直径所在的直线（或过圆心的直线或过半径的直线）
3.如果把圆沿它的某一条对称轴折叠，你能发现什么？
答：两段弧相等；
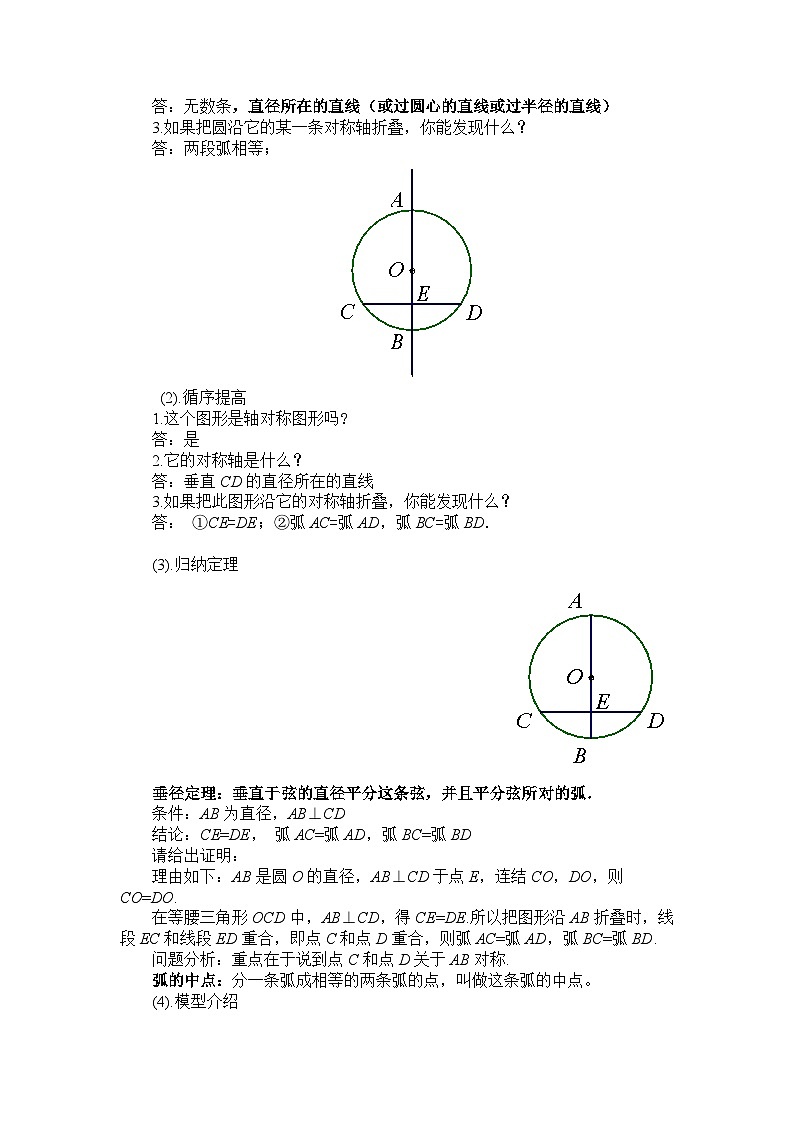
(2).循序提高
1.这个图形是轴对称图形吗?
答：是
2.它的对称轴是什么？
答：垂直CD的直径所在的直线
3.如果把此图形沿它的对称轴折叠，你能发现什么？
答： ①CE=DE；②弧AC=弧AD，弧BC=弧BD.
(3).归纳定理
垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．
条件：AB为直径，AB⊥CD
结论：CE=DE， 弧AC=弧AD，弧BC=弧BD
请给出证明：
理由如下：AB是圆O的直径，AB⊥CD于点E，连结CO，DO，则CO=DO.
在等腰三角形OCD中，AB⊥CD，得CE=DE.所以把图形沿AB折叠时，线段EC和线段ED重合，即点C和点D重合，则弧AC=弧AD，弧BC=弧BD.
问题分析：重点在于说到点C和点D关于AB对称.
弧的中点：分一条弧成相等的两条弧的点，叫做这条弧的中点。
(4).模型介绍


三、讲解新课，探求新知
例1 已知AB，如图，用直尺和圆规求作这条弧的中点．
作法：
⒈连结AB.
⒉作AB的垂直平分线 CD， 交弧AB于点E.
点E就是所求弧AB的中点．
变式训练： 求弧AB的四等分点．
思路：先将弧AB平分，再用同样方法将弧AE、弧BE平分．
（图略）
例2 一条排水管的截面如图所示．已知排水管的半径OB为10，水面宽AB为12，求截面圆心O到水面的距离OC．
思路：
先作出圆心O到水面的距离OC，即画 OC⊥AB，∴AC=BC=6，
在Rt△OCB中，
∴圆心O到水面的距离OC为8．
变式拓展：一段时间以后，排水管内的水面上升，上升后的水面宽度为16，求水面上升的高度.

分析：
第1种情况：水面DE在圆心下方，OC交DE于点F,连结OE.
由DE//AB，得OC⊥DE，则EF=DF=8.
因为OE=10，所以OF= OC-OF=2.
所以FC=2，即水面上升了2.
第2种情况：水面DE在圆心上方，OC延长线交DE于点F,连结OE.
由DE//AB，得OC⊥DE，则EF=DF=8.
因为OE=10，所以OF=6.
所以FC=OC+OF=14，即水面上升了14.
综上所述，水面上升了2或者14.
弦心距：圆心到圆的一条弦的距离叫做弦心距．
小结：
1．画弦心距是圆中常见的辅助线；
2．半径（r）、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：弦长．
注：弦长、半径、弦心距三个量中已知两个，就可以求出第三个．
五、目标训练,及时反馈
1．已知⊙0的半径为13，一条弦的AB的弦心距为5，则这条弦的弦长等于 ．
答案：24
2．如图，AB是⊙0的中直径，CD为弦，CD⊥AB于E，则下列结论中不一定成立的是（ ）
A．∠COE=∠DOE B．CE=DE C．OE=BE D．弧BD=弧BC
答案：C
3．如图，⊙O的直径为10，弦AB长为8，M是弦AB上的动点，则OM的长的取值范围是（ ）
A．3≤OM≤5 B．4≤OM≤5 C．3