2024-2025学年冀教版数学八年级上册期末复习试卷【含答案】

这是一份2024-2025学年冀教版数学八年级上册期末复习试卷【含答案】，共14页。试卷主要包含了下列式子中，是最简二次根式的是，÷的计算结果为，下列计算正确的是，二次根式中字母x可以取的数是，近似数2.1×104精确到，在下列4个实数中，最小的数是等内容，欢迎下载使用。
1．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
2．下列式子中，是最简二次根式的是（ ）
A．B．C．D．
3．÷的计算结果为（ ）
A．B．C．D．
4．如图，在△ABC中，D、E、F分别是AB、BC、CA的中点，图中与△DEF全等的三角形有（ ）
A．0个B．1个C．2个D．3个
5．下列计算正确的是（ ）
A．B．C．D．
6．二次根式中字母x可以取的数是（ ）
A．0B．2C．﹣D．
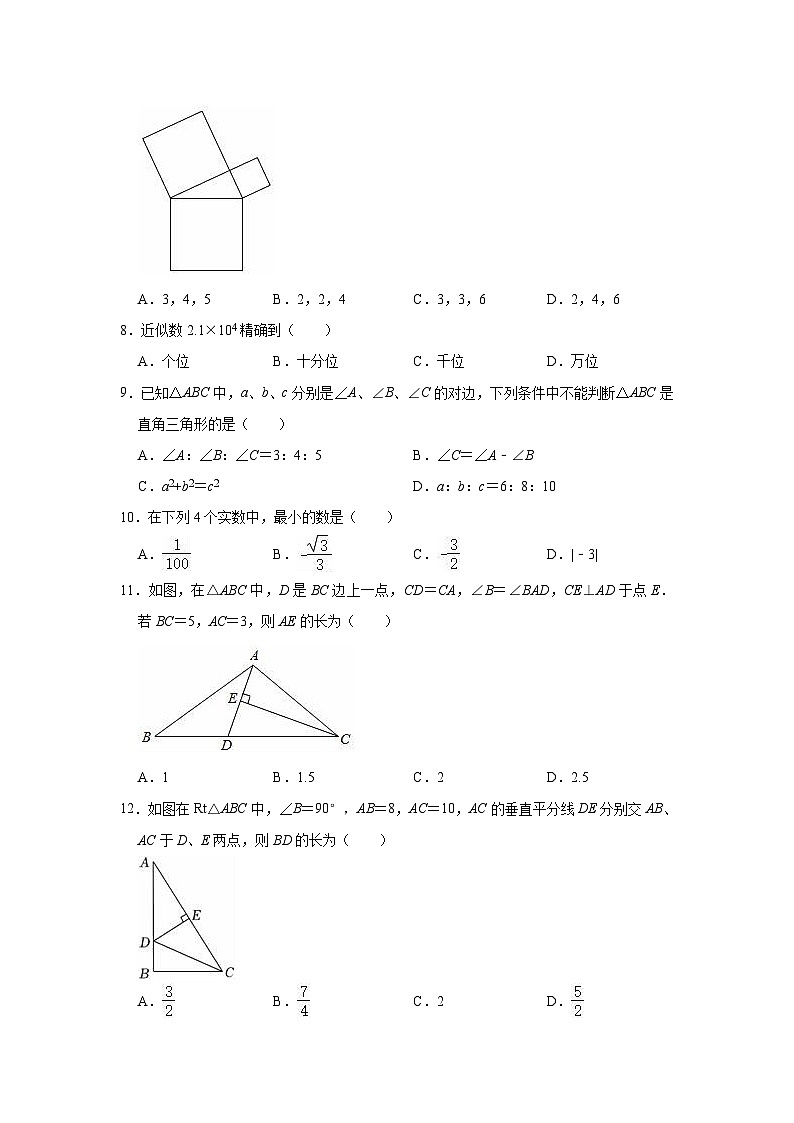
7．如图所示是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案，现在有五种正方形纸片，面积分别是2，3，4，5，6，选取其中三块（可重复选取），按如图所示方式组成图案，使所围成的三角形是直角三角形，则选取的三块纸片的面积不可以是（ ）
A．3，4，5B．2，2，4C．3，3，6D．2，4，6
8．近似数2.1×104精确到（ ）
A．个位B．十分位C．千位D．万位
9．已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件中不能判断△ABC是直角三角形的是（ ）
A．∠A：∠B：∠C＝3：4：5B．∠C＝∠A﹣∠B
C．a2+b2＝c2D．a：b：c＝6：8：10
10．在下列4个实数中，最小的数是（ ）
A．B．C．D．|﹣3|
11．如图，在△ABC中，D是BC边上一点，CD＝CA，∠B＝∠BAD，CE⊥AD于点E．若BC＝5，AC＝3，则AE的长为（ ）
A．1B．1.5C．2D．2.5
12．如图在Rt△ABC中，∠B＝90°，AB＝8，AC＝10，AC的垂直平分线DE分别交AB、AC于D、E两点，则BD的长为（ ）
A．B．C．2D．
13．如图所示，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D，如果AE+DE＝3cm，那么AC等于（ ）
A．2cmB．3cmC．4cmD．5cm
14．随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递40件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件，根据题意可列方程为（ ）
A．＝B．
C．＝﹣40D．＝
15．若分式方程﹣＝2无解，则m的值是（ ）
A．1B．﹣1C．1或﹣1D．0
16．如图，△ABC是边长为2的等边三角形，D，E分别为BC，AC的中点，P是AD上的一个动点，则PE+PC的最小值为（ ）
A．B．C．1D．2
二．填空题（共4小题，满分12分，每小题3分）
17．化简的结果为 ．
18．如图，已知∠A＝∠D，EF∥BC，请在空格上添加一个适当的条件，使得△ABC≌△DEF，则添加的这个条件是 （只要填上一个满足的条件即可，多填不多给分）．
19．如图，在四边形ABCD中，BD平分∠ABC，∠BAD＝∠BDC＝90°，E为BC的中点，AE与BD相交于点F，若BC＝4，∠CBD＝30°，则DF的长为 ．
20．如图，∠AOB＝60°，C是BO延长线上的一点，OC＝7cm，动点P从点C出发沿CB以2cm/s的速度移动，动点Q从点O出发沿OA以1cm/s的速度移动，如果点P、Q同时出发，用t（s）表示移动的时间，当t＝ 时，△POQ是等腰三角形．
三．解答题（共6小题，满分56分）
21．（1）解方程： +＝．
（2）先化简，再求值：（﹣x+1）÷，其中x＝﹣2．
22．如图所示，在公园草地上准备修建一个凉亭，要求凉亭与花坛M、N之间的距离相等，并且与两条小径AB、CD的距离也相等，请你来确定凉亭的位置．
23．计算：（m+2n）（m﹣2n）﹣（m﹣n）（m+8n）．
24．如图，AD是等边△ABC的中线，AE＝AD，求∠AED的度数．
25．冰封文教用品商店欲购进A、B两种笔记本，用160元购进的A种笔记本与用240元购进的B种笔记本数量相同，每本B种笔记本的进价比每本A种笔记本的进价贵10元．
（1）求A、B两种笔记本每本的进价分别为多少元；
（2）若该商店A种笔记本每本售价24元，B种笔记本每本售价35元，准备购进A、B两种笔记本共100本，且这两种笔记本全部售出后总获利不小于468元，则最多购进A种笔记本多少本？
26．如图，在Rt△ABC中，AB＝8，BC＝6，点D从B点出发，沿射线CB方向以每秒3个单位长度的速度运动，射线MP⊥射线CB且BM＝10，点Q从M点出发，沿射线MP方向以每秒a个单位长度的速度运动，已知D、Q两点同时出发，运动时间为t秒．
（1）当t＝2时，△DMQ是等腰三角形，求a的值．
（2）求t为何值时，△DCA为等腰三角形．
（3）是否存在a，使得△DMQ与△ABC全等，若存在，请直接写出a的值，若不存在，请说明理由．
参考答案与试题解析
一．选择题（共16小题，满分32分，每小题2分）
1．解：A、是轴对称图形，也是中心对称图形，故本选项正确；
B、不是轴对称图形，是中心对称图形，故本选项错误；
C、是轴对称图形，不是中心对称图形，故本选项错误；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选：A．
2．解：A选项，原式＝，故该选项不符合题意；
B选项，是最简二次根式，故该选项符合题意；
C选项，原式＝2，故该选项不符合题意；
D选项，原式＝，故该选项不符合题意；
故选：B．
3．解：原式＝÷
＝•x（x﹣2）
＝．
故选：B．
4．解：∵D、E、F分别是AB、BC、CA的中点，
∴DF为△ABC的中位线，
∴DF∥BC，DF＝BE＝EC＝AB，
∴∠EDF＝∠DEB．
在△EDF和△DEB中，
，
∴△DEF≌△EDB（SAS）．
同理可证得：△DEF≌△CFE，△DEF≌△FAD．
故选：D．
5．解：A、原式＝2﹣＝，原计算正确，故此选项符合题意；
B、与不是同类二次根式，不能合并计算，故此选项不符合题意；
C、原式＝3＝3×5＝15，原计算错误，故此选项不符合题意；
D、原式＝8，原计算错误，故此选项不符合题意；
故选：A．
6．解：由题意得，3x﹣1≥0，
解得，x≥，
∵0、2、﹣、中只有2大于，
∴x可以取的数是2．
故选：B．
7．解：由题意可得，三角形各边的平方是对应的各个正方形的面积，
∵所围成的三角形是直角三角形，
∴斜边对应的正方形的面积＝两直角边对应的正方形的面积和，
又∵3+4≠5，2+2＝4，3+3＝6，2+4＝6，
∴选取的三块纸片的面积不可以是3，4，5，
故选：A．
8．解：2.1×104＝21000，
故近似数2.1×104精确到千位，
故选：C．
9．解：当∠A：∠B：∠C＝3：4：5时，则∠C＝180°×＝75°，同理可得∠A＝45°，∠B＝60°，故选项A符合题意；
当∠C＝∠A﹣∠B时，可得∠C+∠B＝∠A，又∵∠A+∠B+∠C＝180°，∴∠C＝90°，故选项B不符合题意；
当a2+b2＝c2时，则△ABC时直角三角形，故选项C不符合题意；
当a：b：c＝6：8：10时，a2+b2＝c2，则△ABC时直角三角形，故选项D不符合题意；
故选：A．
10．解：根据题意得：﹣＜﹣＜＜|﹣3|＝3，则最小的数是﹣．
故选：C．
11．解：∵CE⊥AD于点E，
∴∠CEA＝∠CED＝90°，
在Rt△CEA和Rt△CED中，
，
∴Rt△CEA≌Rt△CED（HL），
∴AE＝DE，
∵BC＝5，AC＝3，
∴BD＝BC﹣CD＝BC﹣AC＝5﹣3＝2，
∵∠B＝∠BAD，
∴BD＝AD＝2，
∴AE＝AD＝1．
故选：A．
12．解：∵∠B＝90°，AB＝8，AC＝10，
∴BC＝6，
∵DE是AC的垂直平分线，
∴CD＝AD，
∴AB＝BD+AD＝BD+CD＝8，
设CD＝x，则BD＝8﹣x，
在Rt△BCD中，CD2＝BC2+BD2，
即x2＝62+（8﹣x）2，
解得x＝6.25．
∴BD＝8﹣6.25＝1.75＝．
故选：B．
13．解：∵BE平分∠ABC，∠ACB＝90°，DE⊥AB于点D，
∴DE＝EC，
∵AE+DE＝3（cm），
∴AE+EC＝3（cm），
即：AC＝3cm，
故选：B．
14．解：设原来平均每人每周投递快件x件，则更换了快捷的交通工具后平均每人每周投递快件（x+40）件，
依题意得：＝．
故选：D．
15．解：去分母得：x+m＝2x﹣2，
由分式方程无解，得到x﹣1＝0，即x＝1，
把x＝1代入整式方程得：1+m＝0，
解得：m＝﹣1，
故选：B．
16．解：如图，连接BE交AD于点P′，
∵△ABC是等边三角形，AB＝2，AD是BC边上的高，E是AC的中点，
∴AD、BE分别是等边三角形ABC边BC、AC的垂直平分线，
∴P′B＝P′C，
P′E+P′C＝P′E+P′B＝BE，
根据两点之间线段最短，
点P在点P′时，PE+PC有最小值，最小值即为BE的长．
BE＝，
所以P′E+P′C的最小值为：，
故选：A．
二．填空题（共4小题，满分12分，每小题3分）
17．解：∵＜＜3，
∴＝3﹣﹣（﹣）
＝3﹣﹣+
＝﹣2．
故答案为：﹣2．
18．解：∵EF∥BC，
∴∠EFD＝∠ACB，
∵∠D＝∠A，
∴当DF＝AC时，△ABC≌△DEF（ASA），
∴可以添加条件：AC＝DF或AF＝CD．
故答案为：AC＝DF或AF＝CD．
19．解：如图，
在Rt△BDC中，BC＝4，∠DBC＝30°，
∴BD＝2，
连接DE，
∵∠BDC＝90°，点E是BC中点，
∴DE＝BE＝CE＝BC＝2，
∵∠DCB＝30°，
∴∠BDE＝∠DBC＝30°，
∵BD平分∠ABC，
∴∠ABD＝∠DBC，
∴∠ABD＝∠BDE，
∴DE∥AB，
∴△DEF∽△BAF，
∴，
∴．
解得：DF＝．
故答案为：．
20．解：分两种情况：（1）当点P在线段OC上时，
设t时后△POQ是等腰三角形，
有OP＝OC﹣CP＝OQ，
即7﹣2t＝t，
解得，t＝；
（2）当点P在CO的延长线上时，此时经过CO时的时间已用3.5s，
当△POQ是等腰三角形时，∵∠POQ＝60°，
∴△POQ是等边三角形，
∴OP＝OQ，
即2（t﹣3.5）＝t，
解得，t＝7．
故答案为： s或7s．
三．解答题（共6小题，满分56分）
21．解：（1）+＝
+＝
2（1﹣x）+5（1+x）＝10，
2﹣2x+5+5x＝10，
7+3x＝10，
3x＝3，
x＝1，
检验：x＝1代入1﹣x2＝0，
故原分式方程的无解．
（2）原式＝÷
＝•
＝•
＝•
＝﹣x（x+1）
＝﹣x2﹣x，
当x＝﹣2时，
原式＝﹣4﹣（﹣2）
＝﹣4+2
＝﹣2．
22．解：如图所示，点P即为所求．
23．解：原式＝[m2﹣（2n）2]﹣（m2+8mn﹣mn﹣8n2）
＝（m2﹣4n2）﹣（m2+7mn﹣8n2）
＝m2﹣4n2﹣m2﹣7mn+8n2
＝4n2﹣7mn．
24．解：∵AD是等边△ABC的中线，
∴∠BAC＝60°，AD平分∠BAC，
∴∠CAD＝∠BAC＝30°，
∵AD＝AE，
∴∠ADE＝∠AED，
∴∠AED＝（180°﹣∠DAE）＝×（180°﹣30°）＝75°．
25．解：（1）设A种笔记本每本的进价为x元，则B种笔记本每本的进价为（x+10）元，
依题意，得：＝，
解得：x＝20，
经检验，x＝20是原方程的解，且符合题意，
∴x+10＝30．
答：A种笔记本每本的进价为20元，B种笔记本每本的进价为30元．
（2）设购进A种笔记本m本，则购进B种笔记本（100﹣m）本，
依题意，得：（24﹣20）m+（35﹣30）（100﹣m）≥468，
解得：m≤32．
答：最多购进A种笔记本32本．
26．解：（1）当t＝2时，DB＝6，
∵BM＝10，
∴DM＝4，
∵△DMQ是等腰三角形，∠DMQ＝90°，
∴DM＝MQ，即4＝2a，
解得，a＝2；
（2）①当AC＝AD时，△DCA为等腰三角形，
∵AB⊥CD，
∴BD＝BC＝6，
∴t＝2；
②由勾股定理得，AC＝＝10，
当AC＝CD＝10时，△DCA为等腰三角形，
∵BC＝6，
∴BD＝4，
∴t＝；
③当AD＝CD＝6+3t时，△DCA为等腰三角形，
∵∠ABD＝90°，
∴AB2+BD2＝AD2，即82+（3t）2＝（6+3t）2，
解得，t＝，
综上所述：t＝2或或时，△DCA为等腰三角形；
（3）当△DMQ与△ABC全等，
①△DMQ≌△ABC，
∴MQ＝BC＝6，DM＝AB＝8，
∵BM＝10，
∴BD＝2或BD＝18，
∴t＝或t＝6，
∴a＝9或a＝1；
②△DMQ≌△CBA，
∴DM＝BC＝6，MQ＝AB＝8，
∴BD＝4或16，
∴t＝或，
∴a＝6或，
综上所述：当△DMQ与△ABC全等时，a＝9或1或6或．